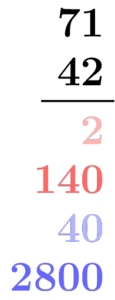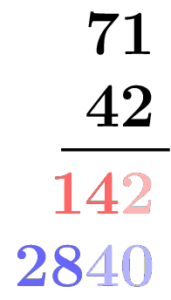By William McCallum
You may have noticed that I am back to publishing regular blog posts! My goal for now is a blog post every second Wednesday. I am now also trying to answer forum questions promptly. I want to thank the readers who took up the slack for the last year and a half in answering questions in the forums. In particular, I’d like to call out abieniek, Alexei Kassymov, and Lane Walker, whose answers were always spot on.
Now to the topic of this post. There has been a lot of talk since the standards came out about what they say about multiple methods for arithmetic operations, and I’d like to clear up a couple of points.
First, the standards do encourage that students have access to multiple methods as they learn to add, subtract, multiply and divide. But this does not mean that you have to solve every problem in multiple ways. Having different methods available is like having different means of transportation available to get to work; flexibility is good, but it doesn’t mean you have to go to school by car, then by bus, then walk, then bike—every single day! The point of having multiple methods available is to encourage students to think strategically about what might be the best method for a given problem, not force them to solve every problem four times.
Second, the different methods are not unrelated; they form a progression, with the ultimate goal being the standard algorithm. For example, when students are first learning to multiply two digit numbers, they might use a rectangle to represent a product such as $42 \times 71$.
This shows the fundamental role of the distributive property in multiplying multi-digit numbers. You have to multiply each base ten component into each other one. Indeed, the same rectangle representation provides a visual proof of the distributive property itself.
At some later point students might just start writing down all the partial products, without using the rectangle to derive them.
Note the correspondence between the rectangle method and the partial product method, indicated by the colors. The first row of the rectangle and shows all the products by the 2 in 42 (in red); the second row shows all the products by the 40 (in blue). The products in the partial product method are grouped in the same way. There are many ways you can order the partial products, but if you group them as I have here, going from right to left in each two-digit number, as in the standard algorithm, you make an amazing discovery: you can add up all the partial products in each group (blue group or red group) in your head as you go along. That’s because, in each case, adding the 2 to the 140 or the 40 to the 2800, there are enough zeroes in the second addend to accommodate the first, so it is easy to write down the sum right away, without writing the addends separately.
OK, so it’s not always quite this easy, because every now and then you will have to keep in mind a bundled unit from the previous step (aka carrying), but you will never have to remember that for more than one step at a time, because each bundled unit gets used up at the next step. So if you invent a notation for remembering the bundled unit (what we used to call “little 1 in the corner” when I was growing up) then you can still avoid writing down all the partial products, and just compute the sum within each group as you go along. You have just created the standard algorithm.
The different methods are not isolated different ways of doing the same thing; they are steps towards fluency with the standard algorithm, fluency that is not fragile because it is supported by understanding.