slope
On Similar Triangles

On Similar Triangles

May 7, 2018

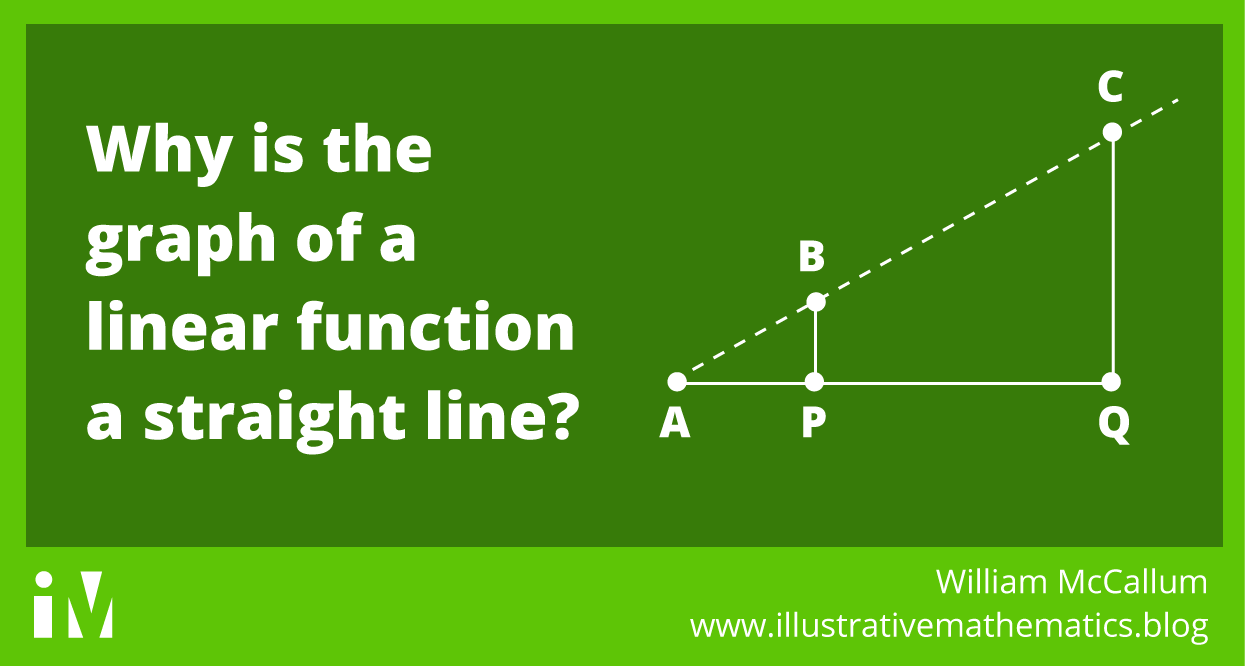
By Ashli Black The fact that a line has a well-defined slope—that the ratio between the rise and run for any two points on the line is always the same—depends on similar triangles. (p.12, 6–8 Progression on Expressions and...

read more
SUBSCRIBE

to the IM Blog and Newsletter

Giveing Tuedsday Heart

Support Free Math Instruction for All Learners

As a nonprofit, we rely on the support of our generous community. Each contribution allows us to reach more classrooms, develop new educational materials, and create opportunities that inspire curiosity and a love for learning.