By Kate Nowak
A thing that I think we did really well in Illustrative Mathematics 6–8 Math was attend carefully to really deep, important things that adults that already know math can easily overlook. For example, what does an equation mean? What does it mean for a number to be a solution to an equation? What does it mean for two expressions to be equivalent? (This is an example of the crucially important foundational understanding that gets short shrift when we rush kids through middle school math.)
Confusingly, the symbol = can mean a few different things.
- If we represent the quantities in a word problem with x + 2 = 3x, we might mean, “What value in place of x, if any, makes each side have the same value?”
- If we decide to see what happens when x is 4, we might write down x = 4. In this case, the = symbol means, “At this moment, we assign the value 4 to x.”
- If we represent two quantities that we suspect are equal no matter their value of x with 4 + 6x – 12 = 2(-4 + 3x) and use properties of operations to rewrite each expression until they are identical to each other, = means an entirely different thing: “I think these expressions are equal no matter what I substitute for x, and I would like to know for sure.”
If you’re reading this you probably realized all of that a long time ago, but none of this is at all obvious to your average 6th grader, or even 11th grader, and 6th grade is where in the common core math standards we are supposed to make a big pivot from arithmetic to algebra.
This is just one task in a 6.EE arc designed to foster deep understanding, but I think it exemplifies the careful approach that we take for the sake of sense making. [student materials] [teacher materials(requires free registration)]

The purpose of this task is to understand that two expressions that are equal for every value of their variable are called equivalent expressions. After the teacher eases students into it, students have a chance to work through the task. The entire point is to contrast x+2 and 3x, which are only equal (the same length) when x is 1, with x+3 and 3+x, which are equal no matter the value you substitute for x. Hey we could have told you x+3 and 3+x are equal no matter the value of x because of the commutative property. I wonder what other properties we can make clever use of. That’s the purpose of the next task.
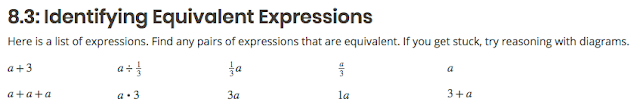
Now, it was hard to choose activities from one lesson to share. This curriculum is multi-faceted and has some super cool stuff. (Actually, the entirety of unit 6 in grade 6 is one of my favorite things in the world, along with the continuation of focusing on the EE standards in grade 7, unit 6. Check it out.) And this lesson is all steak and no sizzle. But getting the unsexy but necessary bits right is something I’m really proud of.
