By Nik Doran
We sometimes use familiar contexts to understand new mathematical ideas, and sometimes we use familiar mathematical ideas to understand what is going on in a context. We do both of these things by looking for parallels between the familiar and unfamiliar structures. I want to highlight two places this happens in the Illustrative Mathematics 6–8 Math curriculum. (It’s easy and free to sign up to see the teacher materials.)
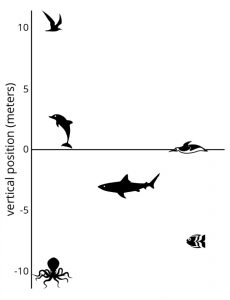 So, if the context is familiar, and the mathematics is new, what does it look like?
So, if the context is familiar, and the mathematics is new, what does it look like?
In this activity, the third in the first lesson of Grade 7, Unit 5: Rational Number Arithmetic, students are asked to use familiar a physical concept—height above or below sea level—to understand and begin to compare the mathematical structure of finding the distance between numbers both above and below zero – subtraction with rational numbers.
What about the reverse? When we use a mathematical structure to understand a context?
We see this at work in Unit 6.7, Lesson 7, Activity 2. Students are asked to examine a table containing the familiar mathematical concept, negative numbers representing reduction or a negative quantity, and reason what these mean in the unfamiliar context of the concession stand problem; that these numbers represent items that are being sold. Since this is grade 6, students are not expected to perform calculations on these rational numbers, only interpret their meaning. They can then use their familiar understanding of the relative size of the rational numbers to reason which items were bought or sold the most.
When writing any problem, it is important to consider what the familiar structure is that can be applied by learners in order to understand what is new. We don’t always explicitly call out the difference, but it’s there in a lot of places in the Illustrative Mathematics 6–8 Math curriculum. Check it out and let me know if you have other favorite examples of either using context to support understanding of mathematical structure and vice versa.
