By Kate Nowak
(co-authored with Kristin Gray)
“Ultimately, the goal of this unit is to prepare students to make sense of situations involving equivalent ratios and solve problems flexibly and strategically, rather than to rely on a procedure (such as “set up a proportion and cross multiply”) without an understanding of the underlying mathematics.”
Illustrative Mathematics 6–8 Math, grade 6, unit 2, lesson 12
We don’t tend to spend much time explaining why we didn’t do things a certain way, preferring to provide a thorough rationale for the approaches we did take. But the choice to not spend curricular time on “cross multiplying” as a technique for dealing with equivalent ratios is sometimes contentious and also illuminates the decisions you have to make when writing a curriculum to address a particular set of standards, so let’s spend a little time on it here.
First of all, what does “cross multiply” mean? Cross multiplying is sometimes invoked as a technique when solving a problem like “A shade of green paint is made by mixing 2 cups of blue paint and 3 cups of yellow paint. If you have 9 cups of yellow paint, how much blue paint should you mix with it to make the same shade of green paint?” The technique is to represent the unknown cups of blue with a letter, let’s say x, write an equation like 2/3 = x/9, and then “cross multiply,” writing 2 • 9 = x • 3 and solving this equation to get x = 6. So, 9 cups of yellow paint can be mixed with 6 cups of blue paint to get the same shade of green paint.
A math curriculum needs to attend to conceptual understanding, procedural fluency, and applications. One implication of attending to conceptual understanding is that you need to help students understand why for every how. So if we were to include cross multiplying as a technique, we would only do it if we developed understanding of why it works.
Take a pair of fractions that are equal but written with different numbers, like 6/9 and 2/3. I can draw a diagram of two rectangles, each representing 1, and partition them into ninths and thirds to show why 2/3 = 6/9:
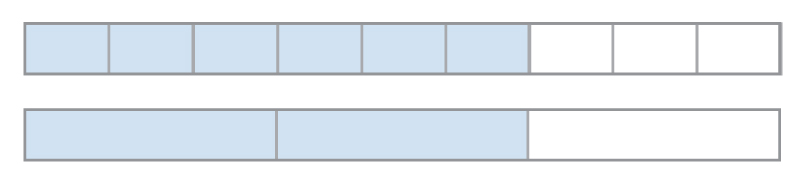
Now let’s cross multiply. It is also true that 6 • 3 = 2 • 9. Where in my diagram can I see why six 3’s must be equal to two 9’s? You can see it, but you have to shift your perspective of what represents “1” (or, said a different way, your perspective of what the fractions represent). It is pretty challenging to explain, based on the meaning of fractions and an understanding of fraction equivalence, why this technique works.
The other way people often justify the move from 2/3 = x/9 to x • 3 = 2 • 9 is by invoking the idea that if you “do the same thing” to each side of an equation, then the equation is still true if the original equation was true. We develop “do the same thing to each side” when the 6.EE conceptual category is studied in its own right in unit 6 and after students understand that the vinculum can represent division. However, students work with equivalent ratios and rates in units 2 and 3, so that contexts developed there can be used for learning new content. The standards just say what students should be able to do at the end of the year; a curriculum makes choices about order and emphasis. And decisions have consequences! So the decision to place the study of equivalent ratios earlier in the year means that we didn’t yet have access to “do the same thing to each side.” One could make a reasonable choice to study equation solving earlier in the year and write a different course.
And back up to that problem about the blue and yellow paint. Why did we use 2, 3, 9, and x to write fractions? Why should these fractions be equal in this problem?
It is a jujitsu move to start with a problem that uses only whole numbers and then write a statement equating two fractions. For people who are already intimately familiar with these ideas, it is useful to represent ratios using fractions. But we are introducing this important and new concept in grade 6, here, and students have worked hard to understand in grades 3–5 that fractions are numbers (3.NF.A) and rely on that definition in their study of fractions. The standards define a ratio as a relationship between two quantities (6.RP.A.1) (and an important ratio that is equivalent to a : b is a/b : 1 (6.RP.A.2)). To suddenly assert that a ratio (2 numbers) is a fraction (1 number) runs counter to this definition of ratio and doesn’t build on the understanding of fractions from grades 3–5. To solve a problem about equivalent ratios by jumping to a statement that equates two fractions fuzzes up the definition of a ratio and the understanding of what a fraction is.
The 6.RP standards are the start of a long chain of experiences and reasoning that results in students in grade 8 understanding that a linear function is characterized by constant rate of change. It goes equivalent ratios and rate ? proportional relationships and constant of proportionality ? linear functions and constant rate of change.
So the approach that we take in grades 6 and 7 to equivalent ratios and proportional relationships is to
- ground understanding in contexts, taking time to develop familiarity with the contexts (mixtures, constant speed, unit price);
- build a collection of representations of equivalent ratios that are used as tools for understanding and tools for problem solving (discrete diagrams, double number lines, tables of equivalent ratios, graphs in the coordinate plane, equations of the form y = kx);
- explicitly show how useful a unit rate is for solving problems—which can be thought of as an entry in a table associated with a “1”, or k in the point (1, k) on a graph;
- work toward using tables efficiently to solve problems (if you think about it, a table with 2 rows and 2 columns looks an awful lot like “set up a proportion”);
- work toward using equations and graphs to represent situations and solve more sophisticated problems.
I know that lots of people are very comfortable teaching cross multiplying, and this change is challenging. But there’s also nothing inherent to the mathematics that requires the cross multiplying procedure. Our approach fosters conceptual understanding, is aligned to the definitions of ratio and fraction in the standards, and is more extensible to future learning.
So how would kids using Illustrative Mathematics 6–8 Math solve the paint problem? I predict they would mostly likely say something like, “Since the recipe needed 3 cups of yellow and I want to use 9 cups of yellow, this is a triple batch of paint. So I’m going to multiply 2 by 3 to get 6 cups of blue.” You might be thinking, “Oh, but this problem is so easy.” Yeah, but I had to draw fraction diagrams about it before, so I picked easy numbers. To see examples of some more on-grade-level problems, check out 6.2.12 or 6.3.7 or 7.2.6 or 7.4.3.
If you’d like to see more details of how “direct proportion problems without cross multiplying” is handled lesson by lesson, I would recommend starting with the scope and sequence for grade 6 and grade 7. In grade 6, you want to look at units 2 and 3. In grade 7, look at unit 2. To see lesson plans, navigate to the teacher materials for those same units. (You’ll have to create a free account and be logged in.)
