By Jared Gilman
As I sat down at my local coffee shop to plan my upcoming 5th grade unit on fractions, a wave of dread spread across my body. I started having flashbacks to last winter, when my students’ frustrations with fractions led to daily meltdowns. Looking back at my lesson plans, I noticed how many reteaching lessons I was forced to add into the middle of my unit. I recalled the painstaking hours of scouring YouTube for videos on the “easiest tricks” and “fastest shortcuts” for adding and subtracting fractions. “My students just didn’t get it,” I thought at the time. This year would be different, I told myself as I gulped down my large iced coffee.
At the time I wasn’t sure why fractions were so painful for my students, but as I reflected on my lessons, I noticed something strange about my curriculum and unit plans. I realized that there was a major lack of a comprehensive introduction to fractions for students. I noted that immediately following the previous chapter test on decimals, the first lesson of the next unit was fraction addition with unlike denominators. Although this lesson hits directly in line with the 5th grade standard (5.NF.A.1), I spent almost no time prior to this lesson discussing fractions, nevermind adding or subtracting them with like denominators. I tried to think back to the last time the students in my current class had worked with fractions on a daily basis, and it must have been almost 9 months ago! I considered that it wasn’t that my students didn’t “get” fractions—as I used to think—but rather it was a reflection of me not knowing where my students were in their understanding before starting this unit. I was constantly playing catch up. All of those reteach days, disappointing quiz grades and meltdowns may have been avoided if I had taken the time at the start of the unit to dig deep into students’ brains and activate their prior knowledge.
In my desire to limit these same mistakes and frustrations, I wanted to take time to learn more about where my students were in their thinking around fractions and provide more context and foundations to lead them to that first lesson of the unit. At first I wasn’t sure which topics were the most important to go over, but fortunately, around this same time, I attended an Illustrative Mathematics professional development session led by Kristin Gray, who provided each teacher with a copy of the Progression Document for the Common Core Math Standards. Reading through the progression with this new lens really helped me to get a sense of what my students should have learned in prior grades and the representations and models they might have used.
I went through the 3rd and 4th grade progressions and pulled out 3 major ideas that built up to the first lesson in my 5th grade unit on adding fractions with unlike denominators. Those 3 ideas were:
- the importance of unit fractions
- fractions as points on a number line, specifically the importance of benchmark fractions
- fraction equivalency
Once I identified the major review areas, I purposefully chose activities to draw these ideas out and assess students’ understanding. To review unit fractions, I chose to start the lesson with a number string. This is essentially a number talk, but each problem given builds on each other and typically gets increasingly more difficult. I asked students to compare two fractions and indicate which was bigger. The order of my questions was this:
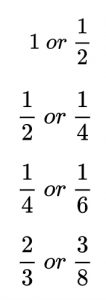
During this activity I also asked students to draw a visual to prove why one was bigger than the other. I noticed that students were able to easily use area models to represent fractions, but struggled to place unit fractions on a number line. This new data helped me gear my mini-lesson and address those points of confusion in the moment. I ended up spending a lot more time on this first number string than I originally planned, but I was able to elicit discussions and ideas which I believe helped set the foundation for the next few days and the entire unit. In response to their confusion around unit fractions, I did a quick mini-lesson I adapted from this lesson on the NCTM website, where students created their own fraction strips out of colored construction paper. Since this was listed as a 3rd grade lesson, I added some rigor by asking students to combine some of the fractions and find relationships between fractions with unlike denominators.
The next day I wanted to push on this idea of number lines and decided to have students create a class fraction number line in the front of the room. Although I was worried about the management aspect in this lesson, my class rocked it and it led to many conversations and debates about the exact placement of fractions and whether fractions were equivalent or not. One interesting debate topic that came out of this task that I wasn’t expecting was whether or not 9/8 belonged on the number line at all. Students had placed 0 and 1 at the ends of the number line, and I saved the 9/8 card for last. Some of my most confident mathematicians argued that the 9/8 card was a mistake and didn’t make sense. This not only opened the door for a unexpected back and forth about fractions greater than 1, but it added another sprinkle of data to inform me about the students’ understanding.
For the last major idea, I decided to lead another number string of adding and subtracting fractions. Based on the 4th grade standards and learning progressions, I started with like denominators, and then moved into unlike, but with simple equivalence that was related to the activity from the day before i.e. ½ + ¼ . This activity was extremely helpful because of the amount of vocabulary review and repetition I was able to build in for each problem in the string.

In the first problem we discussed like denominators, in the second problem we reviewed fractions greater than 1, the third problem elicited another review of equivalence to half, and the final problem touched on fractions with different denominators and how to approach them. This contextualized vocabulary review felt like an added bonus to what was already a meaningful and progressive opening task. I finished this fraction refresher mini-unit by having my 5th graders use their own sets of fraction strips to explore and find as many equivalencies as possible. I pushed my students to look for ones beyond ½ and got a ton of great lists! It was after this lesson, when I saw the genuine joy and excitement that my students were having trying to come up with the most equivalences in the class, that I knew that they were now ready to start the “first lesson” in the fraction unit.

Thinking back on last year, I am embarrassed that I thought one quick review do-now at the start of the unit would be enough. I didn’t realize how many assumptions I was making about my 5th graders remembering what they learned a year ago. This year, although I was hesitant to break from the curriculum and try brand new tasks with my students who love their routines, the results have been outstanding. Whereas last year around this same time, I was dealing with breakdowns and groups of students whose frustrations and confusions deepened with each lesson, just yesterday I had two students ask me if I could “give them more fraction problems for extra credit.” The difference in mood and decreased level of intimidation around fractions have done wonders for my students’ behavior, motivation, and for my own pedagogy about activating prior knowledge going forward. Using the progressions to pull out key concepts, intentionally choosing tasks that matched those big ideas, and being flexible and open with where those tasks might go, have helped my students truly activate their prior knowledge and informed my instruction for the rest of the unit. I suspect that planning my fraction unit next year will feel a lot less stressful.
Call to Action or Next Steps
- Take a look at your next upcoming unit and plan out some tasks that may help to assess and activate your students’ prior understanding.
- Take a look through the Progression Document for the Common Core Math Standards, or watch the Fraction Progression videos on the Illustrative Mathematics website and share something new you learn about fractions from grades 3–5.
- Please share any ideas/feedback if you are in your fractions unit and decide to use number strings, fraction number lines, or other tasks that help to elicit meaningful discussions.




