By Jody Guarino
As a teacher, I constantly wonder how I can elicit student thinking in order to gain insight into the current thinking of my students and leverage their thoughts and ideas to build mathematical understandings for the class.
First, I need a task that will make student thinking visible. Here’s a task from Illustrative Mathematics, Peyton’s Books.
Peyton had 16 books to take on his trip. He lost some. Now he has 7 books. How many books did Peyton lose?
This task requires students to solve a take from change unknown problem. I may gain insight into how my students
- understand and use the relationship of addition and subtraction
- use addition to solve subtraction
- understand the structure of the problem
- count to solve the problem
- use known facts to solve the problem
- decompose and recompose numbers to solve the problem
Second, I need to think about how that task will be situated in order for all students to have access to the task, yet in a way that the thinking isn’t done for them. The problem could be presented to students as it is stated above, simply providing the task statement and space for students to solve the problem. The problem could also be provided with explicit instructions, walking students through a specific procedure, such as:
Step 1: Draw the total number of books Peyton started with.
Step 2: Circle the books Peyton had at the end.
Step 3: Count the number of books that are not circled. Write that number. This is the number of books Peyton lost.
The ways in which this task can be presented are endless and may even seem like insignificant details, but the opportunities each possibility offers in terms of student thinking is quite different. Each of these options will yield significantly different results. Imagine the student work in the step-by-step process. It would likely all look the same. While I might find out which students were able to follow the process and complete the steps, I’m not sure I’d gain any insight into student understanding of the mathematics.
I decided to give students the task as follows:
Peyton had 16 books to take on his trip. He lost some. Now he has 7 books. How many books did Peyton lose? Show your thinking.
Here are a few student responses.

Student A used an addition fact to think about the subtraction fact. If 7 + 9 = 16, then 16 – 7 = 9. Perhaps this is a known fact for the student. Or maybe the student knew 7 + _ = 16, solved that problem, and then thought about the relationship of addition and subtraction. As the teacher, I’m curious how the student thought about 7 + 9.
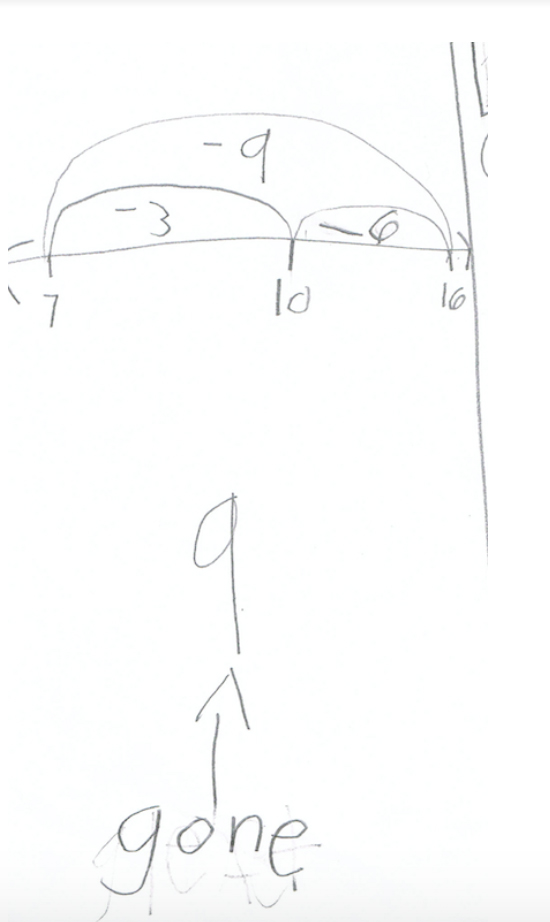
Student B used subtraction to solve the problem. This student began with the subtrahend 16, and then subtracted 6, getting to a friendly 10. The student recorded subtracting 6 on the number line, showing 16 – 6 got the student to 10. Then, the student subtracted 3 from 10, getting to 7. The student kept track of both numbers subtracted, 6 and 3, to determine that he had taken away a total of 9. The student also labeled the quantity of books that were gone, 9. This student seems to have flexibility with numbers, first subtracting to get to a 10 and then subtracting from a 10.
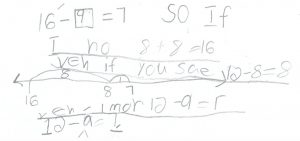
Student C thought about the relationship of the numbers, “I know 8 + 8 = 16.” This student used a number line to show 16 – 8 is 8 and then subtracted 1 to reach 7. The student used the number line in an invented way, something important for me to notice and continue to support.
From a teacher lens, giving students this task in an open-ended way provided me with great insight into student thinking. I know where my students are in their understanding as well as tools to advance their thinking. As I look at the three strategies featured here, I wonder how my students and I might dig further into flexibility of numbers as Students B and C used known facts and 10s to approach the problem. Or maybe we use this work to further investigate operations and the relationship between addition and subtraction. Can addition always be used to solve subtraction? These affordances would not exist if students solved the problem following the step-by-step process above.
From a student lens, my students view themselves as competent problem solvers. I don’t want to send them the message that they are not capable and I need to show them how to do things. Children are sensemakers and I want my students to see themselves as knowledgeable doers of mathematics.
The ways in which students and teachers take up curriculum materials and instruction matters. At Illustrative Mathematics we are committed to creating a world where learners know, use, and enjoy mathematics. While I used an example of a task from IM, this same way of thinking about tasks and student thinking can be applied to other curriculum materials as well.
Next Steps
Next time you look at a lesson from your curriculum, ask yourself how the task elicits student thinking, what you may learn from that thinking, and how it could potentially be adapted to be even better. Share your adaptations in the comments section so we can all learn together and better how we elicit student thinking in every task we use.
