By Kristin Gray
As a teacher, curiosity around students’ mathematical thinking was the driving force behind the teaching and learning in my classroom. To better understand what they were thinking, I needed to not only have great, accessible problems but also create opportunities for students to openly share their ideas with others. It only makes sense that when I learned about routines that encouraged students to share the many ways they were thinking about math such as Number Talks, Notice and Wonder, and Which One Doesn’t Belong?, I was quick to go back to the classroom and try them with my students. It didn’t matter which unit we were in or lesson I had planned for that day, I plopped them in whenever and wherever I could because I was so curious to hear what students would say.
The Learning
While my experiences were invaluable in my own learning about the routines’ structures, questioning, student responses, and discussions, I am quite sure it was not ideal for student learning. The routine was often disconnected from the lesson because it was added at the last minute, flopped because I hadn’t put enough thought into it, and, more times than not, went way too long because I didn’t know what my goal was other than to hear what they had to say. Looking back at all of the times I used my students as guinea pigs, I realized that when I inserted these routines as isolated events, it was more about my learning than theirs.
Over many years of both successful and failed routines, I have learned to focus more on the when and why of a routine than the actual routine itself.
Over many years of both successful and failed routines, I have learned to focus more on the when and why of a routine than the actual routine itself. This focus has helped me see a routine beyond a particular activity at a particular grade level and more as a purposeful structure that can be adapted across all grade levels and math content. While my initial examples will be from grades 6–8, this process is applicable K–12 so don’t stop reading, my K–5 and 9–12 friends.
In order to think about the when and why of a routine, I look at what is happening in the middle of a lesson and plan for what needs to happen beforehand to make the middle more accessible for students. While this may seem out of order in the way we read or think about a typical lesson plan, it was a helpful way of thinking as I designed warm-up routines in the Illustrative Mathematics 6–8 Math curriculum.
The Process
To get a sense of how different routines lend themselves to different purposes, take a minute to read and anticipate how 6th and 7th grade students may respond to each of the following problems.
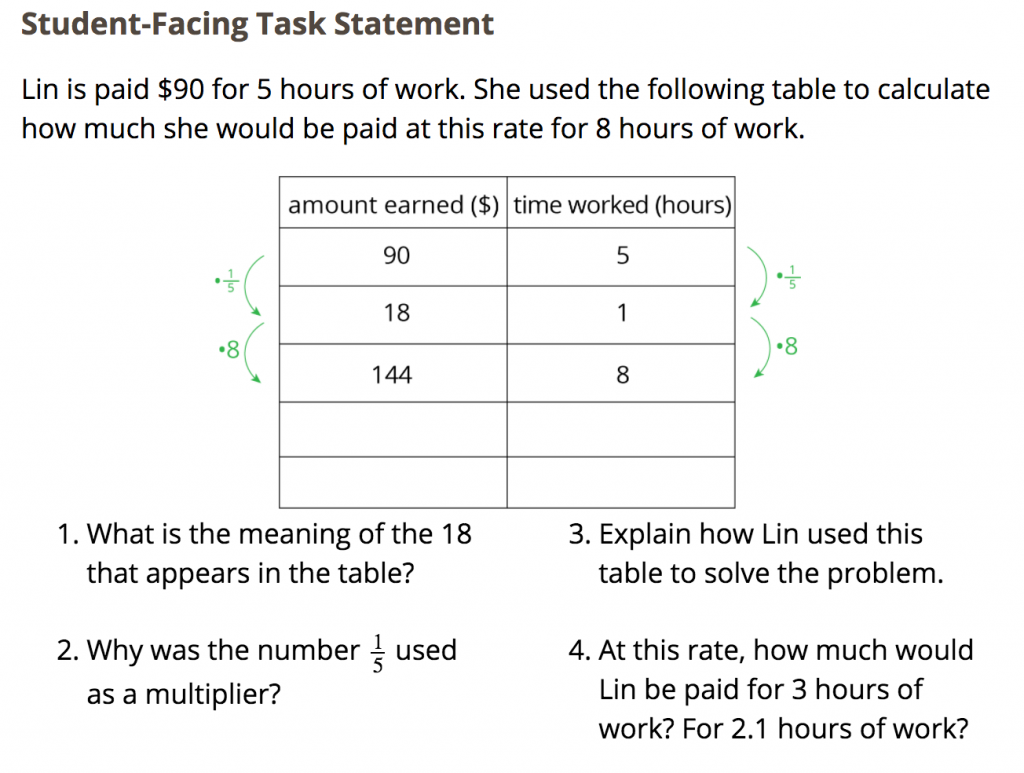
6th Grade, Unit 2: Introducing Ratios
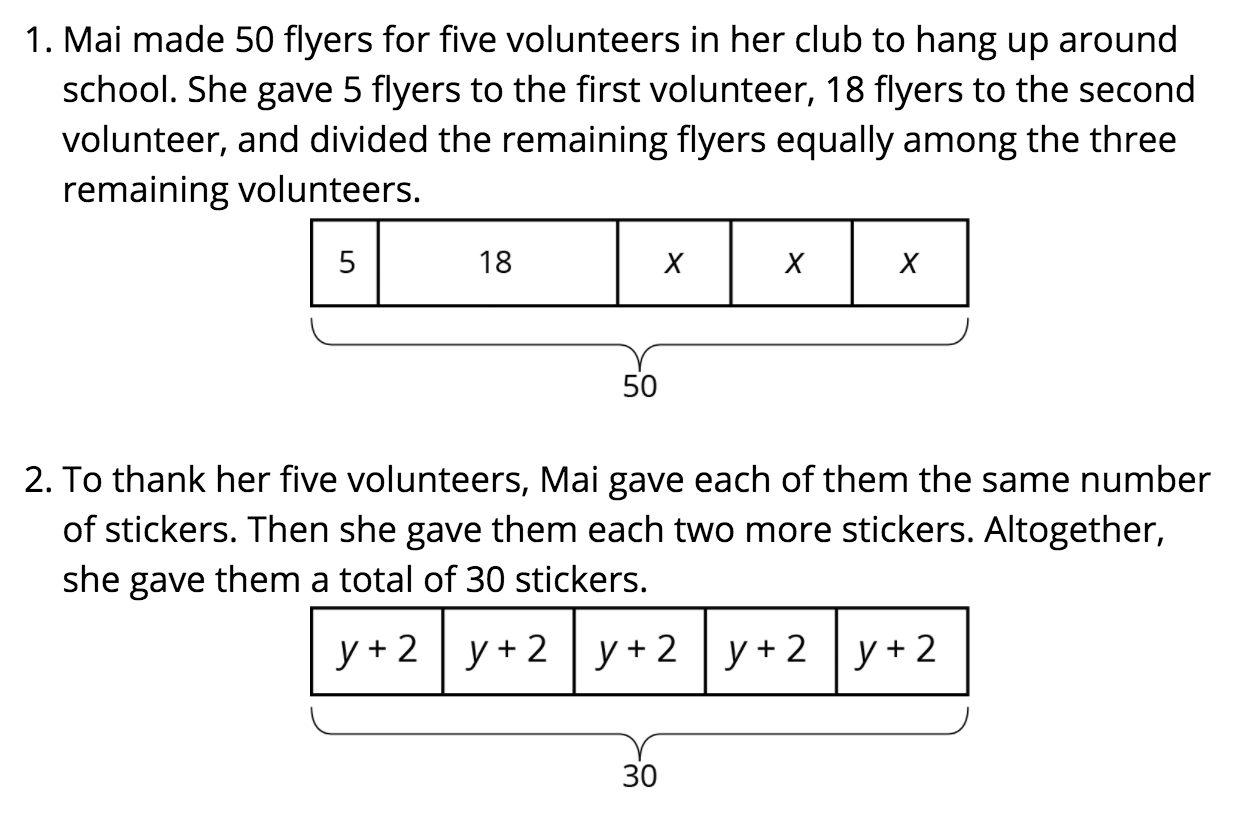
7th Grade, Unit 6: Expressions, Equations, and Inequalities
Now, imagine each of these problems taking place in your classroom.
“While we know there are many ways students could respond, can you identify a point where you anticipate you would have to stop everything to re-explain a particular idea? That is the focus of your warm-up routine.”
Now to determine which routine. For me, the purpose drives my choice of routine. In each of these problems, I see a different purpose for the warm-up. Do you?
In the 6th grade problem, I anticipated computation may be a source of struggle for some students. Since multiplying by a unit fraction may interfere with students making sense of the reasonableness of the amounts in each ratio, I wanted a warm-up routine that addressed computation. In this case, I thought a Number Talk with the goal of refreshing students’ understanding that multiplying by a unit fraction is the same as dividing by its denominator would be helpful to start the lesson. As a subgoal, I kept one factor the same in each set of problems and used fractions with a double or half relationship to encourage students to think about using fractions they know when calculating.
Below is the Number Talk I designed for this lesson:
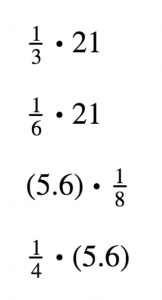
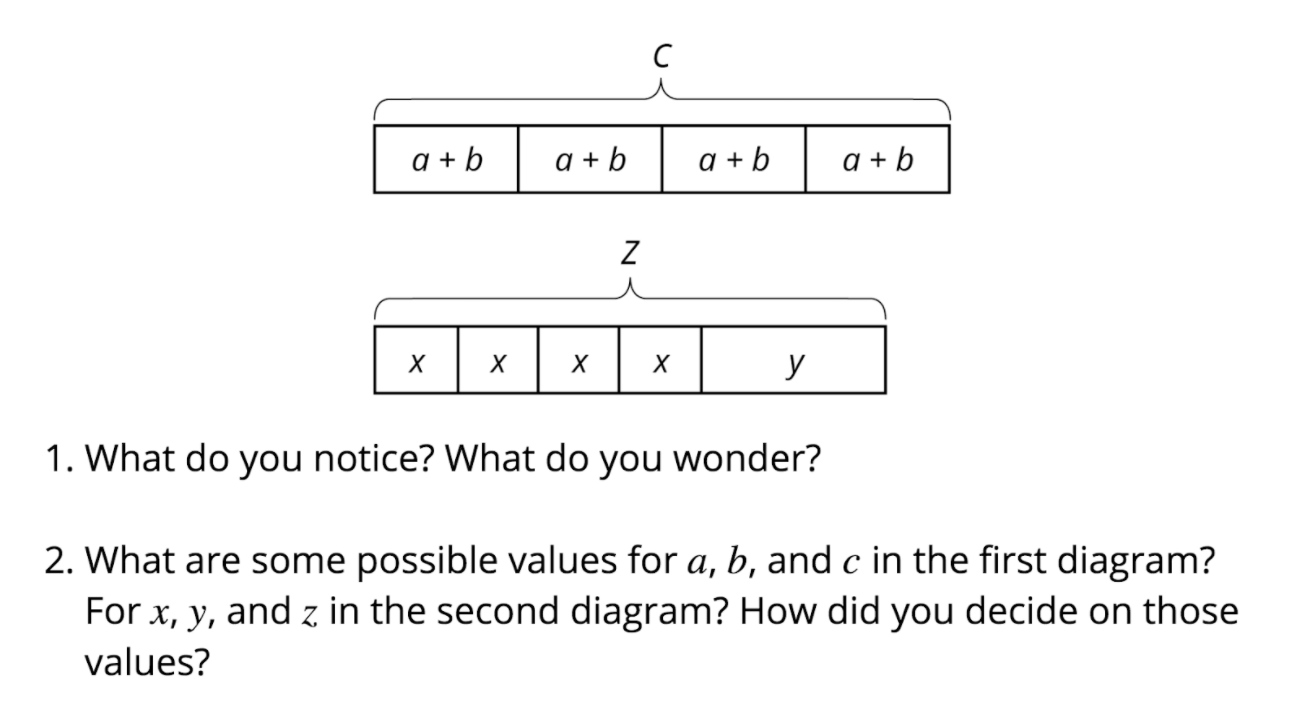
In the 7th grade problem, I anticipated the tape diagram may be something students haven’t seen in a while so a quick refresher would be in order. Since some may not need the review as much as others, I saw it as an opportunity to also jumpstart thinking about the first activity in the lesson. I wanted students to think about the value of different variables based on their relationships in the diagram, so a Notice and Wonder with a focusing question would serve that purpose.
The Application
Let’s try this thinking with some elementary and high school Illustrative Mathematics tasks that do not have warm-ups attached. Look at the problems below, decide which warm-up routine would you use for a lesson that included this activity, and share your warm-up idea in the comments section. We look forward to learning with you and enhancing the tasks on our site!
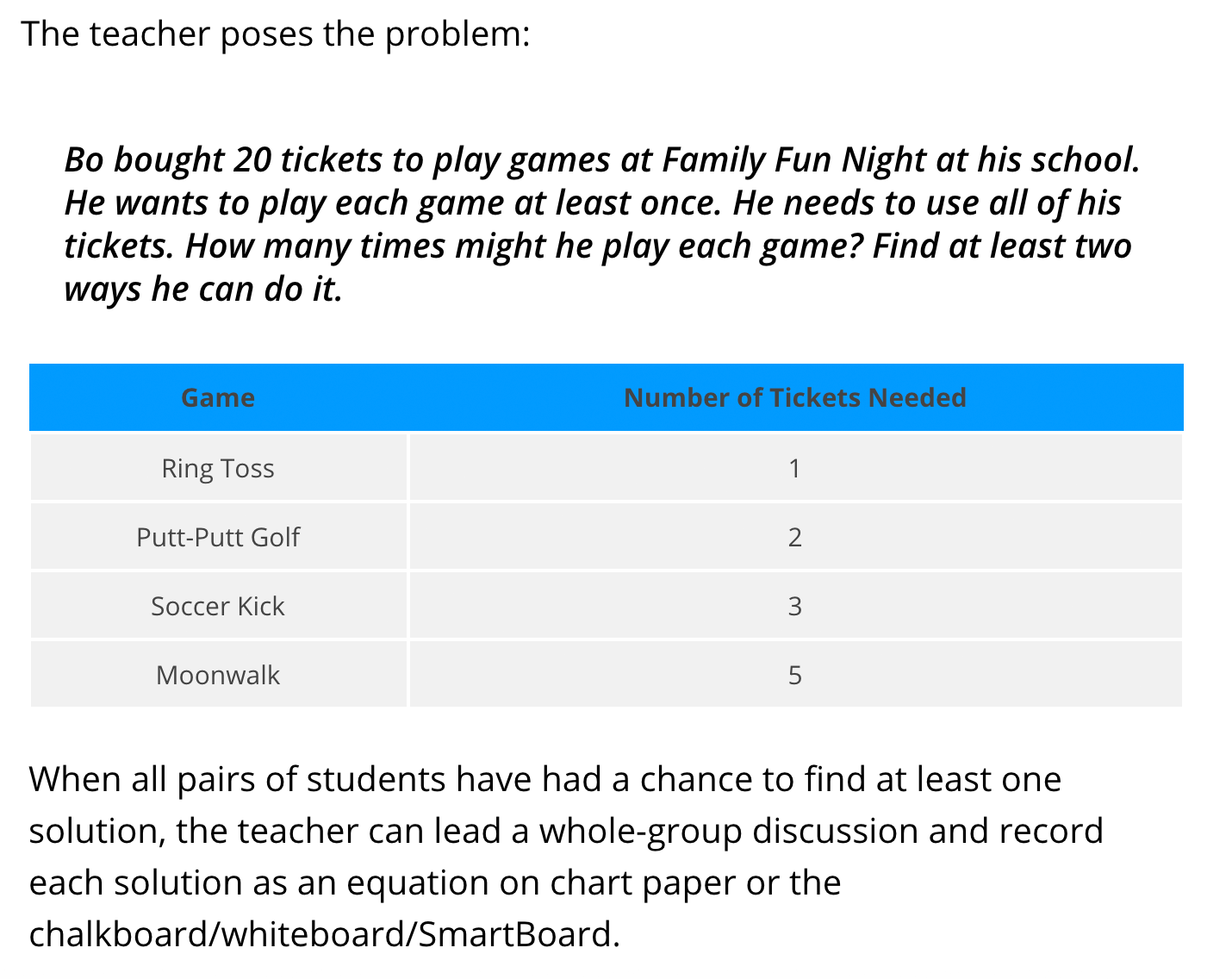
1st Grade Illustrative Mathematics Task: 20 Tickets
3rd Grade Illustrative Mathematics Task: The Geometry of Letters

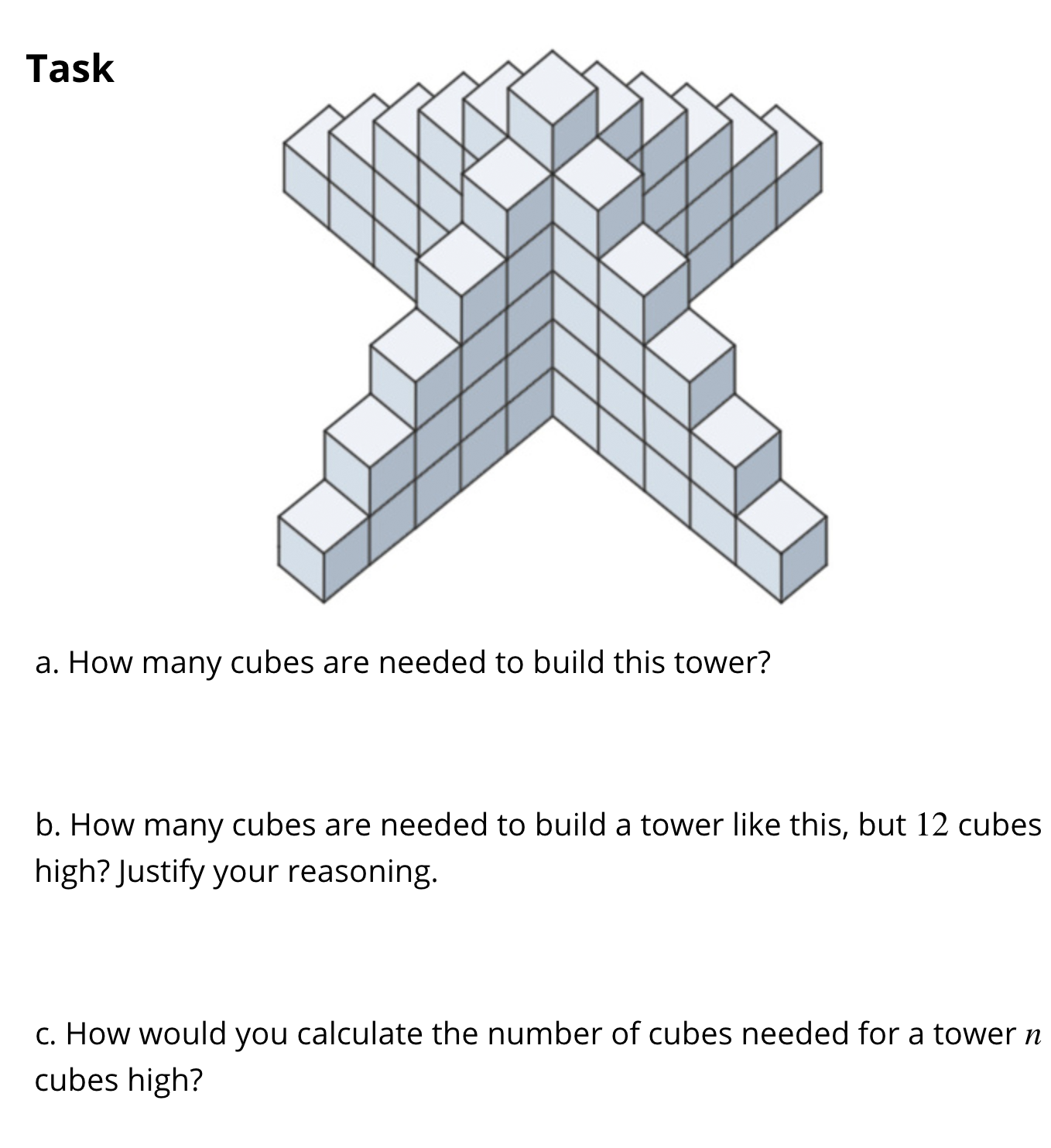
High School: Functions Illustrative Mathematics Task: Skeleton Tower
Next Steps:
In response to teachers requesting more help on implementing Routines, my team at IM has developed a professional learning workshop. Learn More.
