By Jennifer Wilson
One of your students is asked, “What are you learning about today in class?”
How does your student respond?
- “Nothing”
- “Math”
- “The questions on this worksheet”
- “Deciding if two figures are congruent”
During class, one of your students asks you, “Is this going to be on the test?”
How do you respond?
- Pretend like you didn’t hear the question
- With an eye roll
- “Everything I say is going to be on the test”
- “Let’s see how what we’re doing is connected to today’s learning goals”
We know from years of math education research that establishing and sharing learning goals are important for both teachers and students. Even so, we don’t always agree with when and how they should be shared.
- The first of NCTM’s Mathematics Teaching Practices from Principles to Actions is to establish mathematics goals to focus learning (2014, p. 10).
- Before 5 Practices for Orchestrating Productive Mathematics Discussions can be effective, teachers must set goals for instruction (Smith & Stein, 2011, p. 13).
- The first of Wiliam and Thompson’s key strategies for effective formative assessment is clarifying, sharing, and understanding goals for learning and criteria for success with learners (2007, p. 64).
- “The learning target articulates for students what they are to learn and at the same time provides insight as to how students will be assessed” (Kanold & Larson, 2012, p. 49).
Consider the learning goals from Grade 8, Unit 1, Lesson 12. (You’ll have to create a free account and be logged in to view the whole lesson.)

Copyright © 2017 Open Up Resources
How are you using learning goals in your planning?
In your classroom?
Some teachers are required to post a learning goal in their room to reference at the beginning of each class. What about you? Do you post the learning goal? The learning target? Both? Neither?
At Illustrative Mathematics, we talk a lot about inviting learners into the mathematics. The purposeful choice of Let’s issues that invitation.
Let’s decide if two figures are congruent.
The team who worked together to develop the Illustrative Mathematics Grades 6–8 Math curriculum crafted student facing learning goals that invite students to learn more about the work to be done in class each day without giving away the mathematics that will be uncovered through the activities.
By the end of the lesson, though, we want to be sure that students know what mathematics is being uncovered. One way teachers ensure students know what is important to take away from the lesson is through the Lesson Synthesis.

Copyright © 2017 Open Up Resources
Some teachers take the opportunity to share the learning targets during the lesson synthesis: As a result of this lesson, we want students to be able to say,
“I can decide using rigid transformations whether or not two figures are congruent.”
Teachers might ask students to think back through the lesson and write an example in their notes to show they can do this. Then the Cool-down gives students the opportunity to show the teacher that they can, in fact, do this. Or, if they can’t yet, where the student might need support.
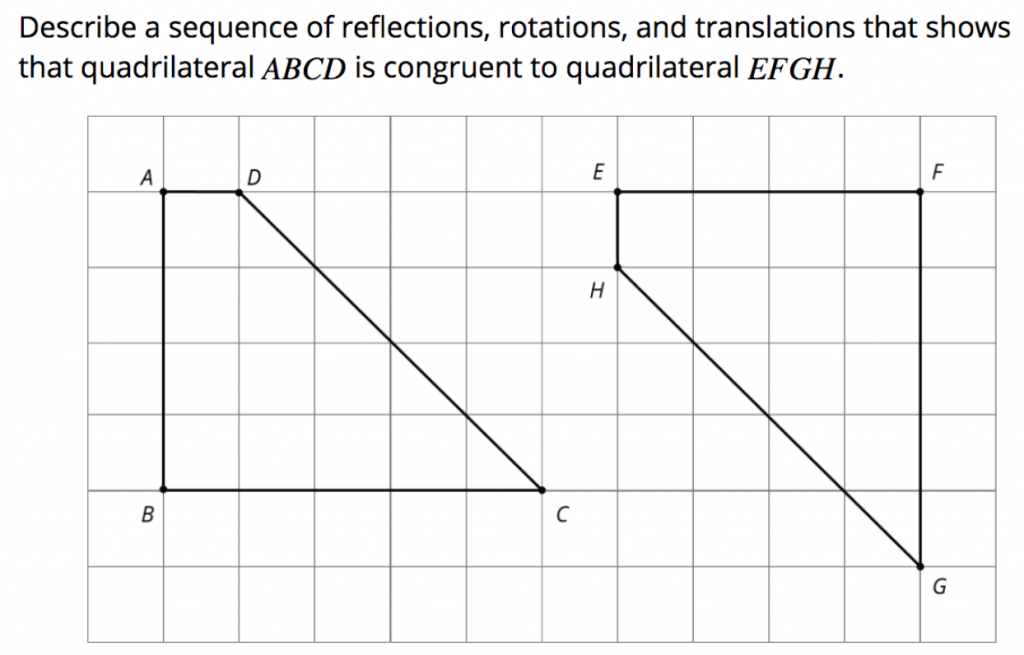
Copyright © 2017 Open Up Resources
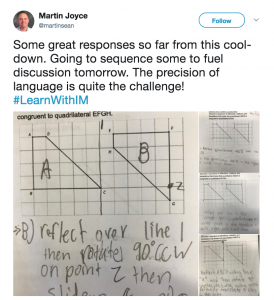 Martin Joyce recently shared some of his students’ work on this Cool-down and his plan to use what students showed they know (and don’t know yet) to begin the next day’s discussion.
Martin Joyce recently shared some of his students’ work on this Cool-down and his plan to use what students showed they know (and don’t know yet) to begin the next day’s discussion.
Each unit has a My Reflections section so that students have easy access to the learning targets. We know of teachers who
- ask students to journal about the learning targets before returning to the next class.
- ask students to use the learning targets as they prepare for the end-of-unit assessment.
- use the learning targets for standards-based grading.

Copyright © 2017 Open Up Resources
Learning goals and learning targets not only help us focus learning, they give our students access to knowing what is important to learn (and what will be assessed) so that they can, in fact, learn what is important.
Next Steps
We would love to hear from you.
- How and when do you use learning goals in your planning and teaching?
- How do your students use them in their learning?
- How and when do you use learning targets in your planning and teaching?
- How do your students use them in their learning?
Learn more about Illustrative Mathematics 6–8 Math.
Kanold, T. D., & Larson, M. R. (2012). Common core mathematics in a PLC at work. Bloomington, IN: Solution Tree Press.
National Council of Teachers of Mathematics (NCTM). (2014). Principles to actions: ensuring mathematical success for all. Reston, Va.: NCTM.
Smith, M. S., & Stein, M. K. (2011). 5 practices for orchestrating productive mathematics discussions. Reston, Va.: National Council of Teachers of Mathematics.
Wiliam, D. & Thompson, M. (2007). Integrating assessment with instruction: Shaping teaching and learning. In Dwyer, C. (Ed.). The future of assessment: Shaping teaching and learning. Mahwah, N.J.: Lawrence Erlbaum Associates.
