By Kate Nowak
This task is the first part of the culminating lesson of unit 2 in grade 8, which is about dilations and similarity. (You will need to create a free teacher account to open the link.) It is a variation on the popular “use shadows and similar triangles to determine the height of a tall thing that it is impossible to measure directly.”
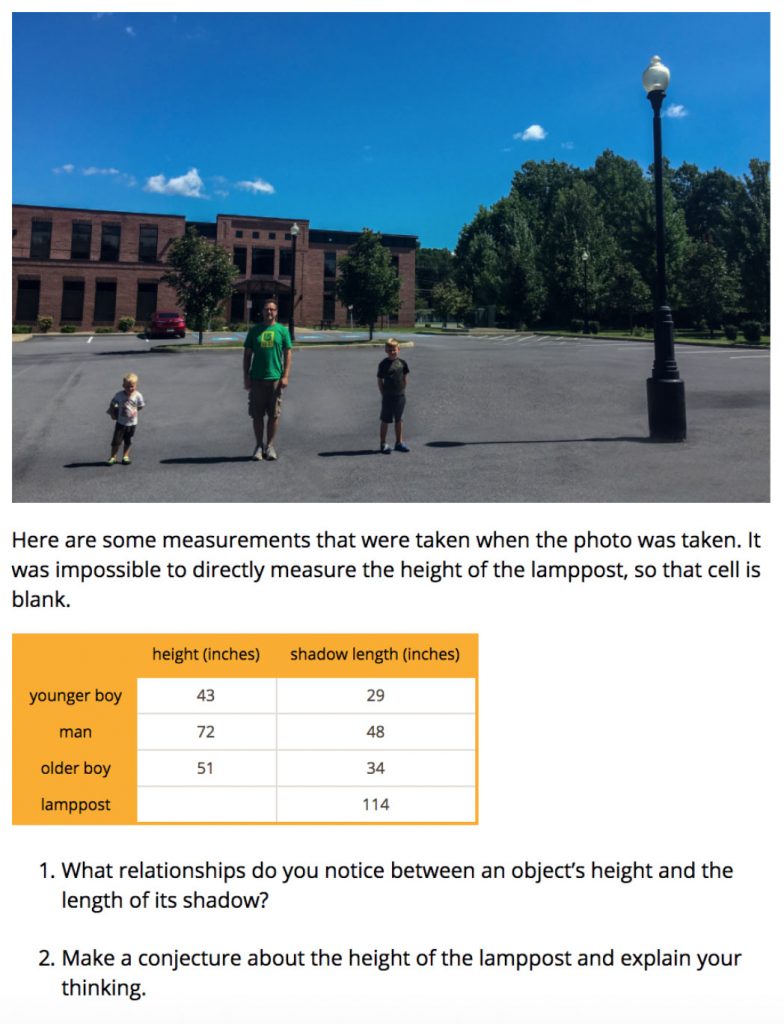
The next activity has students doing a quasi-proof, with the option of then heading outside to indirectly determine the height of a tall object. While developing this lesson, I was noodling over what kinds of things students need to understand in order to be able to tackle it successfully. There are things built into the structure of the task that give them opportunities to draw on things they learned in this unit and previous units. There are 2 of the 3 sides of some similar right triangles right there in the picture, and a table representing a proportional-ish relationship.
I thought back to when I had done activities like this with classes I had taught in the past. There was always a hangup about the sunlight striking all the objects at the same angle. I always felt like I had to kind of do that part for the kids, and they were like “Okay, whatever Miss Nowak” and went along with it.
So, still at my desk, I was thinking about what I could provide in this lesson plan that would help teachers help kids figure that part out for themselves. What would have to be true for the light to not hit the objects at the same angle? The light source would have to be way closer than the sun.
Here is the result of that noodling, a warm-up activity that happens before the task above with the people and the lamppost. These pictures were taken on my desk (looking the cleanest it ever has) and on the sidewalk outside my apartment, and I’m a little proud of them.

After students have a chance to notice and wonder things, we suggest that the teacher display this image to facilitate conversation:

Hey look, the sun hits these 3 objects at essentially the same angle. Why would that be? Cool cool.
There are many great things about Illustrative Mathematics 6–8 Math, but one of my favorites is that a bunch of people had the time and the space to think through how the classroom materials themselves could help ideas make more sense to kids. I didn’t always have that time when trying to design activities while also being a classroom teacher (sorry, former students!) but I’m glad that teachers and kids using these materials get to benefit from the time and space our team had to noodle things through.
Next Steps
Click here to learn more about Illustrative Mathematics 6–8 Math for your school or district.
