By William McCallum
In everyday language, $\frac{a}{b}$, $a\div b$, and $a : b$ are all different manifestations of a single fused notion. Here, for example are the mathematical definitions of fraction, quotient, and ratio from Merriam-Webster online:
Fraction: a numerical representation (such as $\frac34$, $\frac58$, or 3.234) indicating the quotient of two numbers.
Quotient: (1) the number resulting from the division of one number by another (2) the numerical ratio usually multiplied by 100 between a test score and a standard value.
Ratio: (1) the indicated quotient of two mathematical expression (2) the relationship in quantity, amount, or size between two or more things.
The first one says that a fraction is a quotient; the second says that a quotient is a ratio; the third one says that a ratio is a quotient. So, by reflexivity and transitivity of “is,” these are all the same thing! (OK, there is that curious word “indicated,” so I’m exaggerating, but let’s move on.) These definitions are not wrong as descriptions of how people use the words. For example, people (including mathematicians and teachers) say things like “mix the flour and the water in a ratio of $\frac34$.” If you have a firm grasp of the underlying concepts this fusion of language is not a problem.
However, it might not work for children just being introduced to this tangle of ideas. Let’s start with ratios. In a grade 6 lesson in the IM curriculum, which introduces ratios, students use diagrams to represent recipes for powdered drink mix.
They write the ratio as $4:1$. Later, they consider doubling the recipe, and might draw two copies of this diagram side by side and write the ratio as $8:2$. Writing these ratios as fractions might puzzle students, since it would seem to suggest that $\frac82$ is twice as big as $\frac41$.
What about the relation between fractions and quotients? In grade 3, students understand fractions as being built out of unit fractions. For example, $\frac53$ is the point on the number line that you get by dividing the interval from 0 to 1 into 3 parts and taking 5 of those parts. The following diagram from the fractions progression illustrates this.
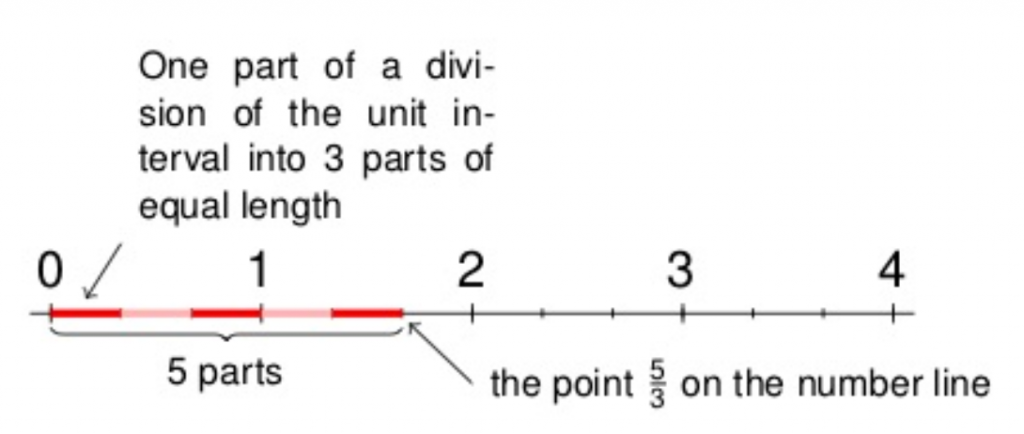
Two years later, in grade 5, students learn that $\frac53$ is equal to $5\div 3$. Here $5\div3$ is understood to be the amount each person gets when you share 5 things equally among 3 people. I don’t think the connection between $\frac53$ as a number on the number line and $5\div3$ as an equal share is obvious. Of course, I can check the connection in this case by taking 3 copies of the number on the number line and getting 5. But there’s a difference between seeing that something is true and seeing why it is true.
Let’s consider the general case. If you share $a$ things among $b$ people, why does each person get $\frac{a}{b}$? One way to share, which students sometimes try first, is to deal out the things until you don’t have enough to go around, then break the remaining ones into equal pieces. It’s not at all clear why everybody gets $\frac{a}{b}$ under this scheme. But another way to share is to take the first thing, divide it into $b$ equal pieces and share those out, then do the same with the second one, then the third, and so on. With this way of sharing you can see that each person gets a total $a$ pieces of size $\frac1b$. So they have $\frac{a}{b}$.
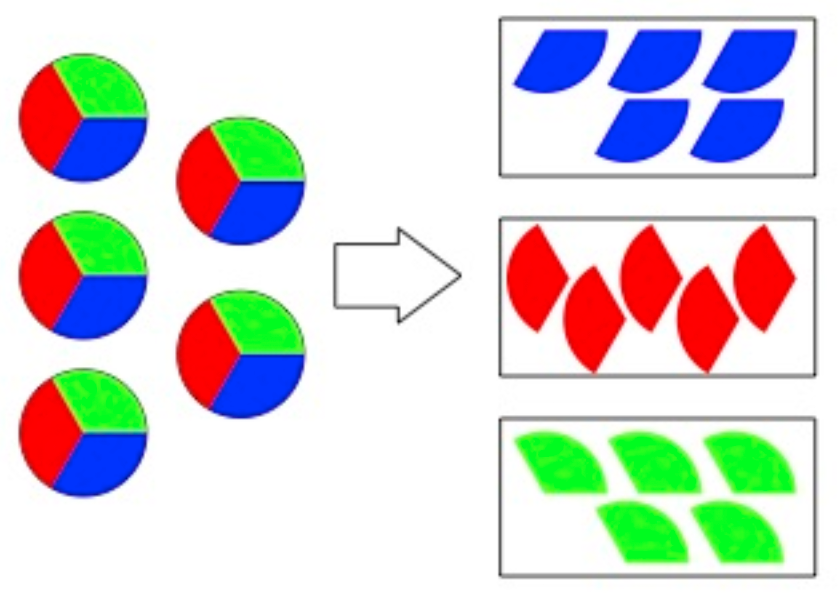
For many adults the notion of fraction and quotient are so fused that they are often puzzled when I ask them why $\frac53 = 5\div3$. In fact, some people tell me this is true by the very definition of $\frac53$. For them, I turn the question around: why is your $\frac53$ the same as the point on the number line indicated in the diagram? Whatever your definition, there is something to understand here, and there is no reason to expect that students will automatically acquire that understanding without help.
In the end, all these notions, as well as the notions of derived quantity and derived unit, are encapsulated into the idea of a rate. If the ratio of miles traveled to minutes elapsed is $5:3$, then the rate is $5\div3 = \frac53$ miles per minute, or 100 miles per hour (don’t try this at home). I often wonder if one reason why so many children (and adults) end up thinking of fractions as a mysterious morass is that we don’t take the time to disentangle all these ideas. I’m looking forward to doing that in the preK–5 curriculum we are working on.
Next Steps
- A lot of these ideas are explained in the fractions progression.
- Try asking your colleagues $\frac53 = 5\div3$. It leads to great conversations.
- Learn more about the LearnZillion Illustrative Mathematics 6–8 Math curriculum here.
Mathematical images shown in this post are excerpted from Open Up Resources Grade 6 – 8 Math by Open Up Resources used under CC BY 4.0. Download for free at www.openupresources.org.
