By Charles Larrieu Casias
The number line is an anchor representation that threads through the entire middle school curriculum. For this blog post, I want to focus on a creative use of the number line in grade 8 to explore scientific notation and irrational numbers. Let’s zoom into a lesson.
In Unit 7, Lesson 10 of grade 8, students learn that the speed of light (or electricity) has different speeds through different materials. These speeds tend to range between $2 \times 10^8$ meters per second and $3 \times 10^8$ meters per second. There are many ways to plot these values on a number line, but since this unit is chiefly concerned with powers of 10, it makes sense to look at a portion of the number line broken into 10 segments going from $0 \times 10^8$ to $10 \times 10^8=1 \times 10^9$. That gives this number line:
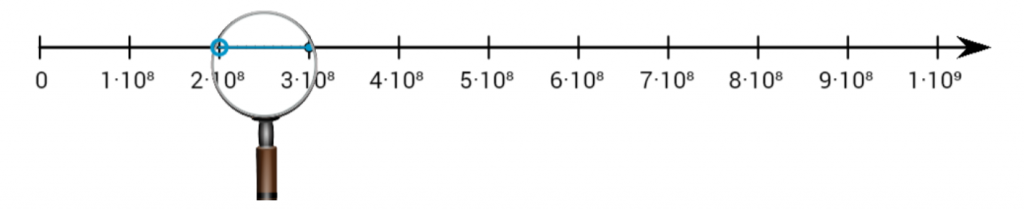
This level of precision isn’t good enough to discern the different speeds of light very well, so we zoom in! The digital student version has a lovely magnifying glass that zooms into the region between $2 \times 10^8$ and $3 \times 10^8$ and subdivides that region into 10 congruent segments:

This zooming number line provides some intuition about what it means to look at more and more decimal places.
The next unit picks up on this idea of zooming into number lines to find more decimal places of irrational numbers and certain rational numbers like $\frac{2}{11}$. I’m probably not supposed to play favorites, but one of the cleverest, most brilliant pieces of design in the curriculum is the path towards irrational numbers in grade 8, Unit 8.
One confusing way to introduce irrational numbers is by their definition. If “Dedekind cuts*” or “infinite, non-repeating decimal expansions” are your first words to a group of eighth graders, you’re going to have a bad time. Instead of starting from a confusing definition and trying to convince students that these numbers exist, it is better to start with an approach where students come across these numbers naturally and investigate their other properties later. Students already know how to find areas of squares like these by decomposition or surrounding with a larger square and subtracting areas of triangles:

You don’t have to convince students that these squares have sides and that those sides have lengths. Square roots have an intuitive, geometric meaning, and analyzing their numerical properties comes later.
In later lessons, students return to zooming number lines to examine the decimal expansions of $\frac{2}{11}$ and $\sqrt{2}$ to get the sense of what it means for a number to have an infinite decimal expansion. Try them out!
It’s beyond the scope of the course to prove that the square root of 2 is irrational, but zooming number lines help students get comfortable with concepts of limits and scientific notation. That’s pretty impressive for eighth grade mathematics.
*Research more about the construction of the real number line. It’s fascinating how something so intuitive as a continuum of numbers could be so technical to define rigorously. For example, check out this part of a video that explains Dedekind cuts or this video about how Georg Cantor proved that the rational numbers are countable while real numbers are uncountable.
Next Steps
- Check out Unit 8 in more detail. It’s fun to see how the unit progresses to give a feel for irrational numbers from a geometric point of view.
Mathematical images shown in this post are excerpted from Open Up Resources Grade 6 – 8 Math by Open Up Resources used under CC BY 4.0. Download for free at www.openupresources.org.
