By Kristin Gray
There are some standards I think we do such a great job developing in early elementary, but never revisit explicitly when students learn about different numbers such as fractions and decimals. I blogged about this in reference to even and odd numbers last year, but this past week I have found another:

Early elementary spends SO much time building understanding of the relationships between 1s, 10s and 100s, but I don’t think we do this standard justice as students build their understandings of fractions and decimals.
Leigh’s grade 5 math class just started their work with decimals. To help students make connections to what they learned last year, she and I went back and brushed up on where the students should be in terms of the grade 4 CCSS. It is always so interesting to me how the CCSS authors chose to put decimals in the NF strand in grade 4 because students are learning that decimals are just another way to write a fraction with a denominator of 10 or 100. Building on that understanding, the decimal work then moves to the NBT strand in grade 5 as students begin operating with them. Those are the little, thoughtful details in the standards that I really appreciate.
In the first lesson or two of the unit, Leigh picked up where the students left off in the curriculum last year – shading 10 by 10 grids in a game called Fill Two. In this game, students only work with tenths and hundredths so in subsequent lessons she introduced thousandths on the same grid, with each small square now partitioned into 10 smaller pieces.
To be confident of the path we were on with decimals, Leigh and I met to revisit the CCSS. We both felt the students were doing 5.NBT.A.1 in a conceptual way, but we were never really making the understanding explicit with students. Since there wasn’t a great place in the curriculum for this, we went to Illustrative Mathematics, found this task, and built a lesson around it.
We opened the lesson with this Which One Doesn’t Belong? to see how students related the representations, in particular, how they talked about the picture since the task had something similar.
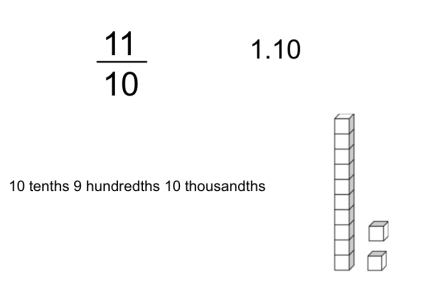

They came up with some really interesting comparisons and everyone saw the picture of base 10 blocks as 0.12 and “not even close to 1,” which the others were. This is where I think the lack of attention we give the standard above is really apparent. I think students learn each small cube is 1/100, so each skinny tower is 1/10, but are never pushed to think about what other values they could represent. How quickly they forget K–2:).
We then did a Notice and Wonder with the image from the task before they jumped in to work on the task prompt.

They did a great job trying to get into Jossie’s head, so we let those ideas sit there as we gave them 3 minutes of individual work time to begin the full task. After time to work with a partner, we came back together to discuss Jossie’s reasoning and the different values the picture could represent.
As we anticipated, many of the students said that Jossie got the tenths and hundredths pieces confused.


So polite in her disagreement, I love it!
Then, one student explained her reasoning below:

After her explanation, I asked the rest of the class what they thought about how tens and hundreds are related versus tenths and hundredths. It was a great discussion of how tens build to hundreds but hundredths build to tenths. My summary here doesn’t do a bit of justice to how the students were talking about the math.
I collected their possible values for the picture and recorded them on the board.

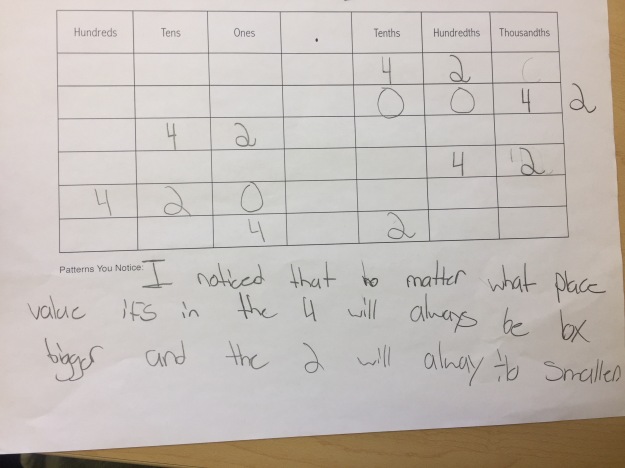
Students took these values and put them into a place value chart to look for patterns:
Some noticed the 4 and 2 were constant in each number and moved around:
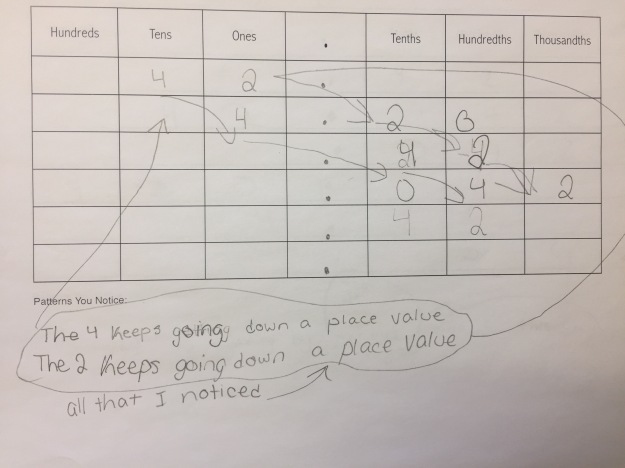
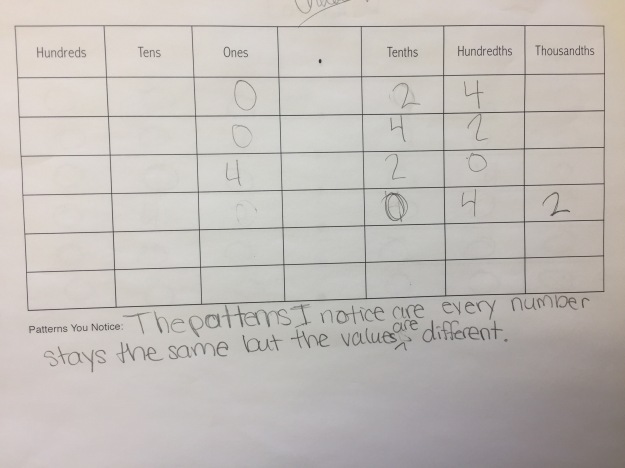
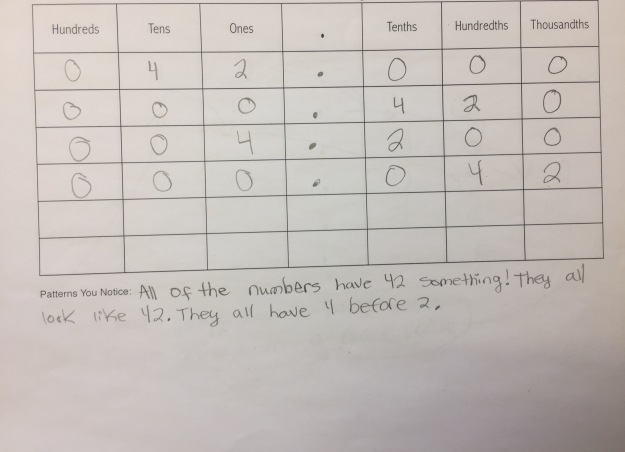
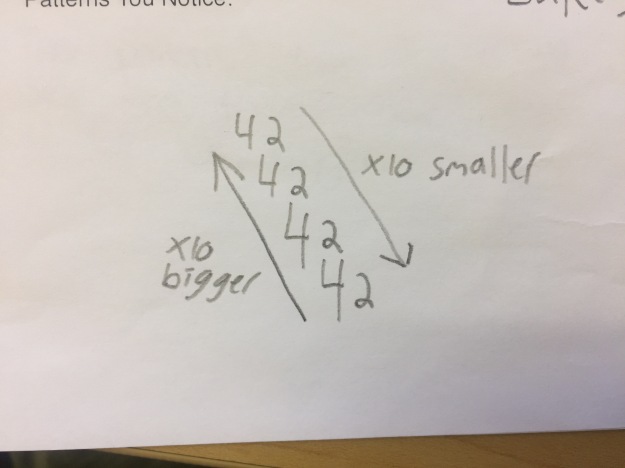
Some students recognized those movements as multiplying or dividing by 10s:
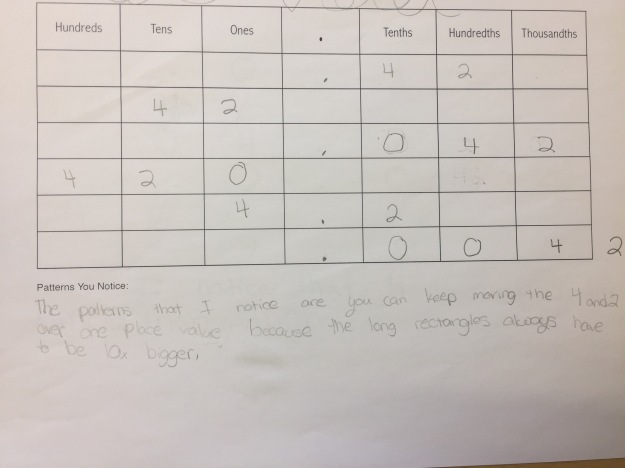
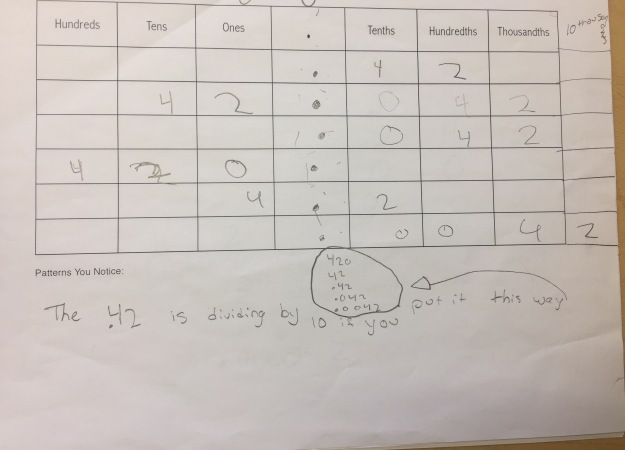
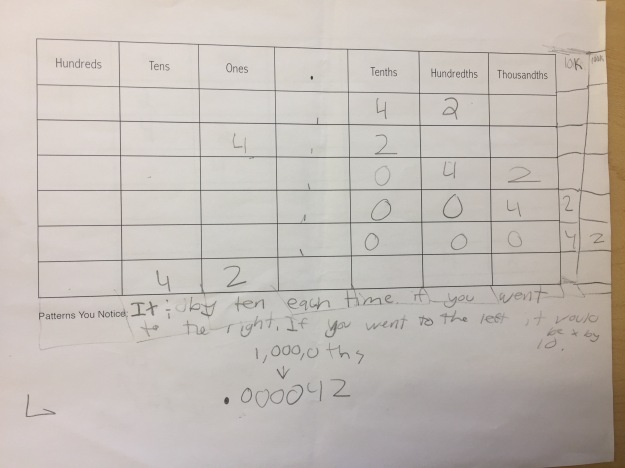
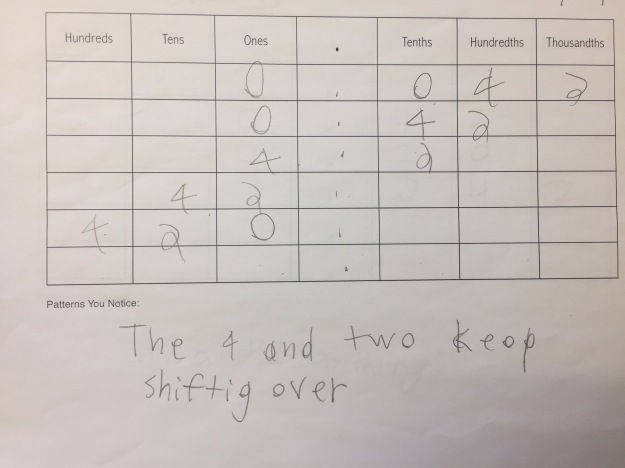
These last two examples are the ones that really seem to get at the standard and something we want to connect the previous examples to build toward: