Time to start a new unit! What do you need to know before your students enter the room?
NCTM’s Principles to Actions names several productive beliefs about assessments that will promote mathematical success for all. At the top of the list is that the “primary purpose of assessment is to inform and improve the teaching and learning of mathematics” (82).
The pre-unit assessments in the IM 6–8 Math curriculum are intended to do just that. The questions are diagnostic, addressing key skills and understandings that a student may leverage into success in the upcoming unit. The standards assessed in each problem may be from previous units or grade levels, including elementary grade levels. The problems help teachers identify what earlier concepts and skills are most critical for students to be able to apply in the upcoming unit, and reveal students’ current mathematical understandings. Teachers are then able to use this information to plan.
This is a departure from more traditional pre/post tests that mirror one another. These tests assess concepts and skills that will be learned over the course of the upcoming unit. This practice may decrease access for many of our more marginalized student populations. They may mistakenly believe they should know content before it has been addressed in class. It can be deflating to have the first experience with new content tinged with failure. Additionally, some students may have already had experiences that allow them to meet end-of-unit benchmarks before the unit even begins, calling into question what students should do during class. Pre-assessments are an issue of equity.
Figuring Out What Students Need To Know—and Why
Student mathematical understandings should build over the course of the unit, so the first step is to figure out what students already know.
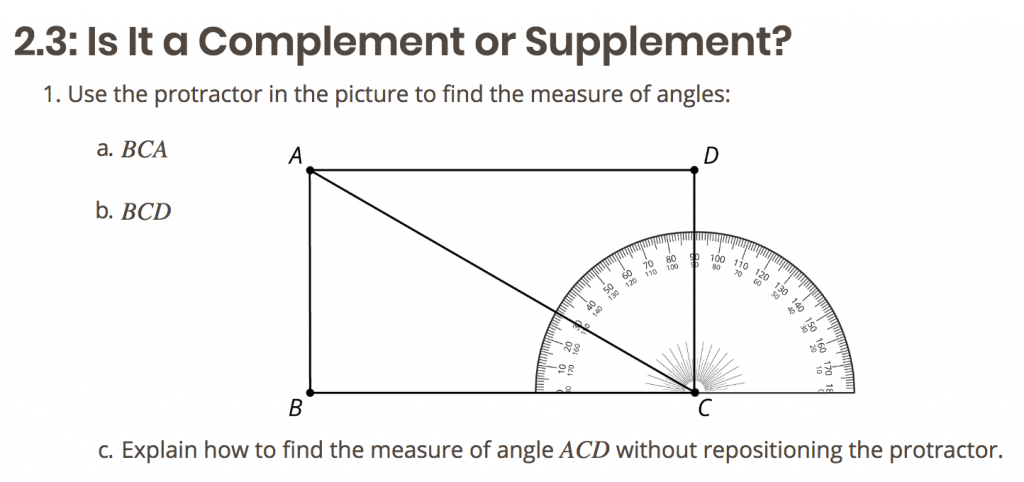
Here is an example of a task from the diagnostic pre-unit assessment for Grade 7, Unit 7 (Angles, Triangles, and Prisms):

Grade 7, Unit 7 Pre-Unit Assessment: Question 2
This question most directly assesses standard 4.MD.C.6: Measure angles in whole-number degrees using a protractor. The assessment narrative provides some quick insight into why work from earlier grades is being assessed:
[bctt tweet=”Throughout the unit, students are expected to measure angles with a protractor in order to make conjectures such as “vertical angles are equal.”” username=”IllustrateMath”]
The following task, from the unit (Grade 7, Unit 7, Lesson 3), illuminates the need for students to be able to accurately and efficiently measure angles.

Without being able to measure angles, students may stumble with this task—and many others throughout the unit. Students might focus more on the act of measuring than the intended learning goal: learning about vertical angles.
How would you support a student working on the Vertical Angles task who did not successfully measure the angles on question 2 of the Pre-Unit Assessment? What other information about the student would you want to take into account?
Figuring Out What To Do
If a large number of students answer the same Pre-Unit Assessment problem incorrectly, it may feel tempting to pause instruction, creating a gap between the assessment and the first lesson. Instead, look for opportunities within the upcoming unit where the target skill can be addressed in context.
For students who struggled with angle measurement in the example above, some possible actions include:
- At the launch of the task, ask students to brainstorm important things to consider when measuring with a protractor.
- Work with a group of students at the start of independent work time, or monitor certain students more carefully.
- Add more opportunities to practice the skill later, with some additional practice problems, or adapt or scaffold tasks from the curriculum.
Working on these skills in context will not only promote greater transfer of the skill, but there may be some intrinsic motivation: students have a need to be able to measure angles for the Vertical Angles task in Lesson 3.
Opportunities to provide scaffolds may happen in an early-in-the-unit task that does not explicitly require the skill. The following task appears in the lesson directly before the Vertical Angles task.
From Grade 7, Unit 7, Lesson 2
Student need to know how to read a protractor in order to be successful with this task, but they do not need to know how how to orient or position the tool until the next day. This tasks offers an opportunity to preview the skill for students that struggled with orientation—lining up one angle along the “0” line, or positioning a vertex in the appropriate place, etc. Planning for this deliberate preview of the skill may translate into greater success in the subsequent lesson.
Strong performance on the Pre-Unit Assessment means students are well prepared for the work ahead. Teachers will still need to tune their instruction to address the needs of different learners, including those that may have already had experience with the unit’s content. Teachers will still need to give regular formative assessments and plan with intention.
5 Steps to Using the Pre-Unit Assessment Effectively
Most of the Pre-Unit Assessments are 7 questions, providing a curated and manageable amount of data. Steps 1–3 are about figuring out what students need to know, and why. Steps 4 and 5 are about figuring out how to adjust instruction.
- Print out the Pre-Unit Assessment and try to solve the questions yourself! How do you anticipate students might solve the questions?
- Identify the standards assessed using the assessment narrative.
- Read through the rest of the assessment narrative to learn more about why these skills are important.
- Look for opportunities in the unit’s lessons and tasks to work on the skills and concepts from the Pre-Unit Assessment.
- Collaborate with your colleagues—other grade level team members, special educators, math coaches, etc.—about what student thinking is anticipated, and how to prepare students for the work ahead.
Next Step
How will you use the Pre-Unit Assessments to inform and improve the teaching and learning of mathematics? We would love to hear about your experience. You can share your pictures, blog post links, and reflections in the comments section below, or on Twitter using our #LearnWithIM hashtag and tagging @IllustrateMath!
