I asked my 15-year-old what she learned today at school. She paused for a moment and then answered, “What did you learn at school today?”
It took me a while to think about what I had learned (which will make me more patient when I ask her again tomorrow), and then I remembered and shared with her:We are working with some teachers who are using the Illustrative Mathematics 6–8 Math curriculum. The 7th grade teachers are in Unit 1, Scale Drawings. They are working with scale drawings and maps. Today I learned to look more closely at the scale given for a map.
For example, look at the following for a moment. What’s the same? What’s different?
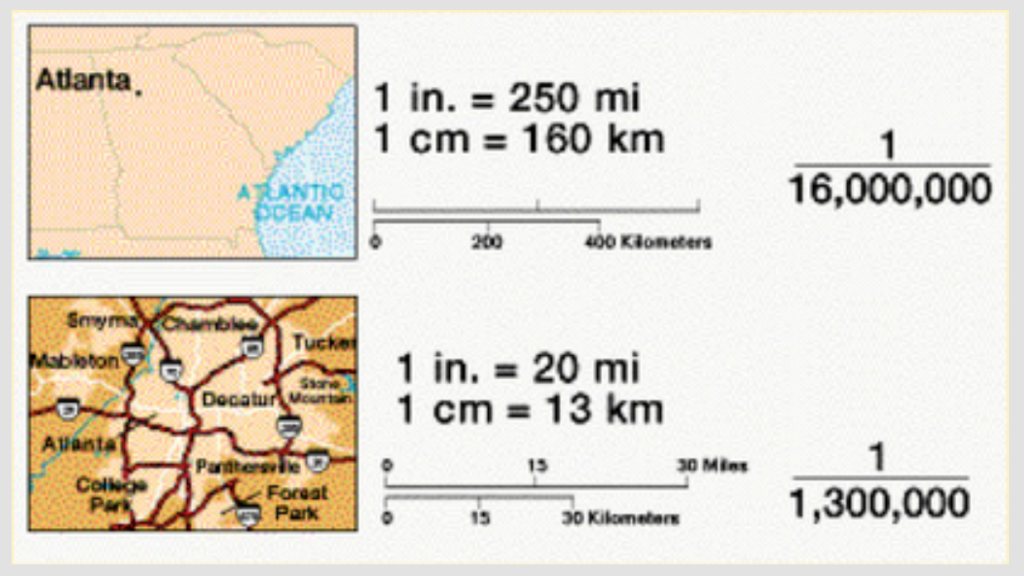
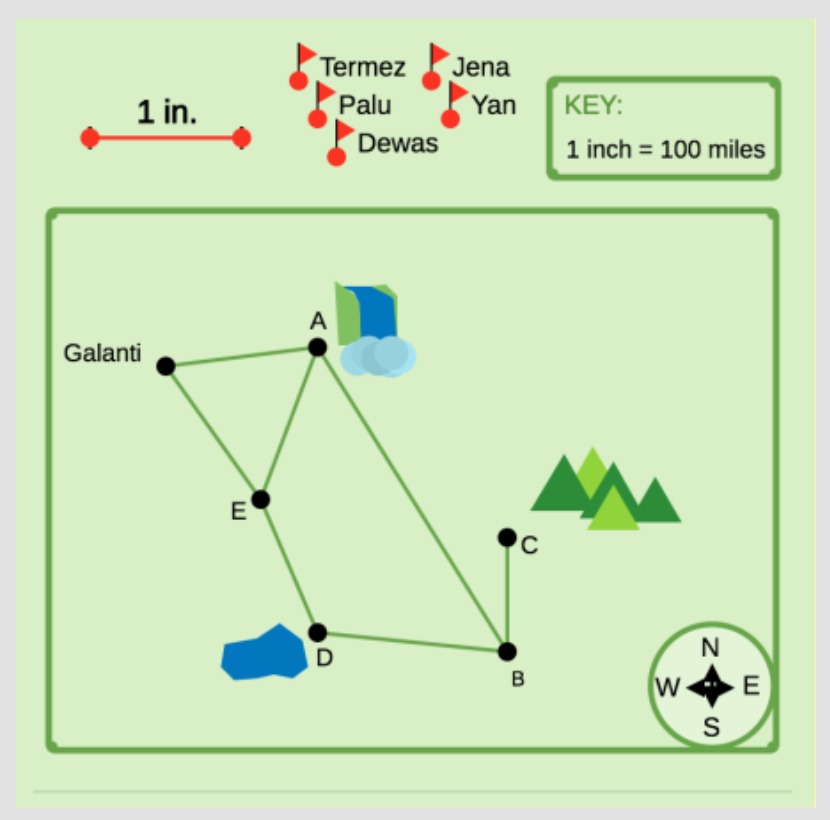
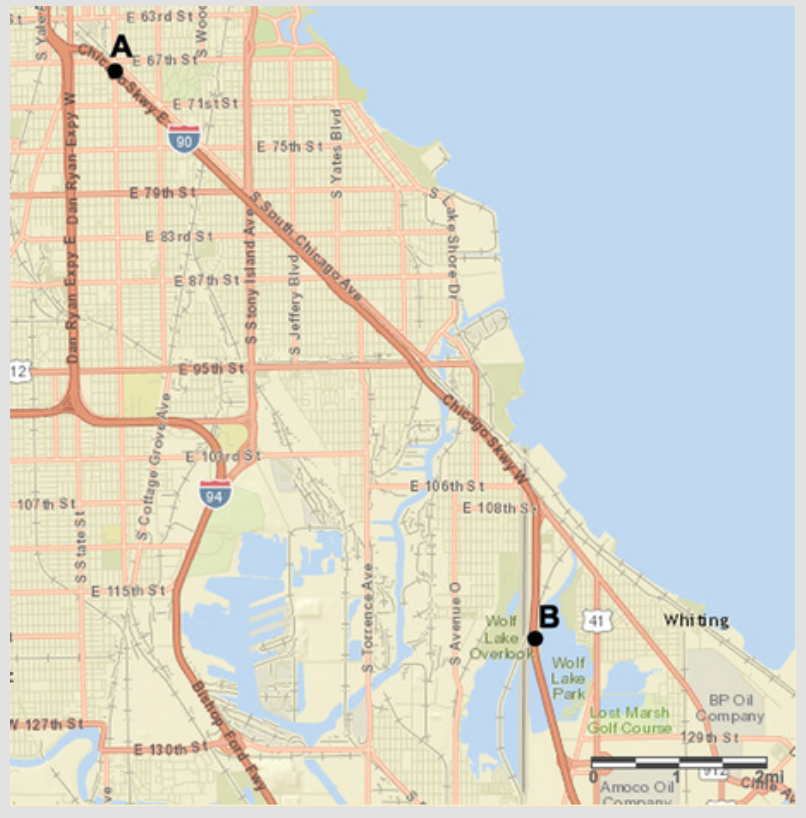

The last two are from IM 6-8 Math, currently available at im.openupresources.org and our IM Certified™ partner, LearnZillion.
What’s different about the scales on the last two?

The standard for mathematical practice about attending to precision (MP6) says: “Mathematically proficient students try to communicate precisely to others. They state the meaning of the symbols they choose, including using the equal sign consistently and appropriately.”
I hadn’t noticed how frequently people record scale using an equal sign. I’m not sure that we would have noticed a difference if we had not been looking at so many questions about scale next to one another. We were trying to find some assessment items for standard 7.G.A.1, the 7th grade standard about scale, and discovered that many of those we found included a scale in the form of “1 cm = 100 miles.” I’ve looked at lots of maps, and I never noticed the incongruity of saying that 1 cm equals 100 miles. We don’t really mean that 1 cm equals 100 miles, right? Not in the same sense that we say 4 quarters equals $1, or 3+4=7. Is there any wonder that our students misuse the equal sign?
The Illustrative Mathematics curriculum is careful to say that 1 centimeter represents 100 miles in the scale drawing. The word represents may be longer than a symbol like the equal sign, but it more accurately shows the relationship. In this case, precision isn’t about efficiency, but accuracy.
Next Step
And so the journey continues. I am grateful for the authors of this curriculum, who help me attend to precision and for my daughter, who makes me think and share about what I’m learning. What are you learning to pay closer attention to as you teach mathematics? I look forward to hearing from you in the comments or at #LearnWithIM.
