NCTM has called for structural and curricular changes in high school mathematics. Learn about how IM’s high school curriculum is aligned with the vision put forth by NCTM to end tracking, implement effective targeted instructional supports, and broaden the focus of teaching high school mathematics beyond college and career readiness.
In April of 2018, the National Council of Teachers of Mathematics published Catalyzing Change in High School Mathematics, a book which focuses on inequities in high school classrooms. While reading this text, we highlighted several calls to action that correspond with our own design decisions, including: ending tracking, implementing effective targeted instructional supports, and broadening the focus of teaching high school mathematics beyond college and career readiness. In this blogpost, we will address how the IM Algebra 1, Geometry, Algebra 2 curriculum aligns with these three proposals.
Catalyzing Change suggests that schools should provide a single pathway through the essential concepts. Instead of grouping students into honors, standard, and fundamentals, teachers should have curricular resources that support them to meet the needs of all students in heterogeneous classes. The IM Algebra 1, Geometry, Algebra 2 curricular materials include both pedagogical and content additions for differentiating materials in two directions. For every lesson in all three courses, there are extension questions available for students who are ready for more. These extensions provide greater depth to the grade-level material rather than seeking to accelerate students. There are also suggestions for supporting all students (anticipated misconceptions) and particular groups of students (students with disabilities and students learning English).
Differentiated support in the classroom will be sufficient for most students, but there are cases where students arrive at high school with significant gaps in their K–8 math education. Catalyzing Change states (and we agree) that requiring these students to spend their first year of high school on prerequisites will limit their options and opportunities. Instead, the IM Algebra 1, Geometry, Algebra 2 curriculum offers a just-in-time extra support class to be taken concurrently with Algebra 1. Each lesson in the extra support course is aligned with a lesson in Algebra 1, so students review and practice prerequisite skills specifically designed to support their success in their Algebra 1 class. This allows all students access to the grade-level curriculum, keeps them on track to have course options senior year, and boosts their confidence in their math abilities which creates a more equitable dynamic in the Algebra 1 course.
While it is essential that students are prepared for post-secondary college and career opportunities, Catalyzing Change asserts that these are not the sole goal of high school mathematics. Instead, the authors of Catalyzing Change expand the purpose of school mathematics to include understanding and critiquing the world. One of the principles that guided the development of the IM curricular materials is that students should encounter examples of a mathematical concept in various contexts before the concept is named and studied as an object in its own right. Students see mathematics as a way to ask and answer questions about situations familiar to their worlds. During such activities, students get to experience aspects of modeling, but it is important that students learn to problem solve in ways that mirror the problems they might encounter outside of school. The IM Algebra 1, Geometry, Algebra 2 curriculum also includes modeling prompts, which are open-ended tasks where students complete more or all of the modeling cycle by problem posing, formulating a model, computing, interpreting results, and validating conclusions.
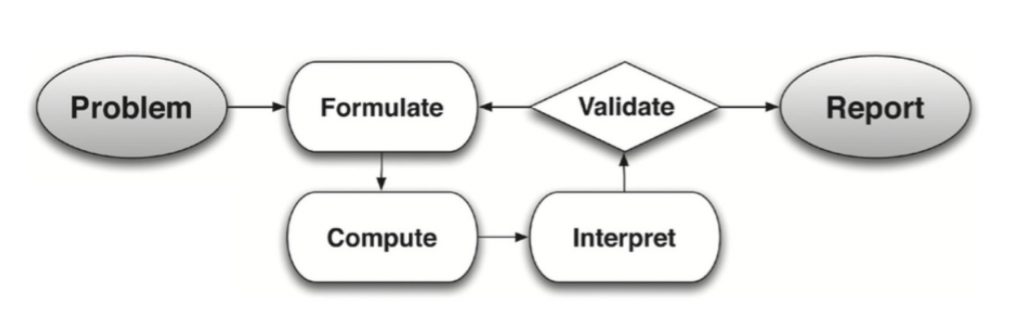
We’re happy to see the authors of Catalyzing Change calling for changes that we believe in. We’re excited to share the IM Algebra 1, Geometry, Algebra 2 curriculum. We hope that it will help students (and teachers!) know, use, and enjoy mathematics.
Next Step
Possible next steps include:
- Read Catalyzing Change with your PLC
- On your own or with colleagues, analyze equity practices within your school. Who has access to on-grade level mathematics? Who has access to the highest level mathematics classes offered at your school?
- What is the focus of your school’s math classes? Do students get the opportunity to model with mathematics? How could you incorporate aspects of mathematical modeling?
