Multiplication is vexation,
Division is as bad;
The Rule of Three doth puzzle me,
And Practice drives me mad.
(old nursery rhyme.)
Some people might answer that multiplication is repeated addition. For example, $5 \times 7$ is 7 added 5 times: $7 + 7 + 7 + 7 + 7 = 35$. One problem with this is that it is possible to get confused about the number of additions. There are only 4 plus signs in the equation, so did I really repeat the addition 5 times? This confusion is particularly acute when I am trying to explain why $0 \times 7 = 0$. According to multiplication-is-repeated-addition, this is 7 added to itself 0 times. Well, okay, I’m not going to do any additions, but don’t I still have the 7 that I started with? Wouldn’t that make $0 \times 7 = 7$? Or would it be 0 because I don’t have any 7s? This confusion is about how to do the multiplication; it could be cleared up by a conceptualization of what multiplication is. (For those who are inclined to abstract mathematics, Jason Zimba has written a tongue-in-cheek proof that multiplication is not repeated addition.)
In the standards, students learn in grade 3 to “interpret $5 \times 7$ as the total number of objects in 5 groups of 7 objects each.” This is the equal groups way of thinking about multiplication. There is a big difference between this and repeated addition: equal groups is a way of thinking, whereas repeated addition is a way of doing. That is, repeated addition tells you how to calculate $5 \times 7$. But it doesn’t really tell you why you are doing the calculation except “that’s what I told you to do.” By contrast, the equal groups way of thinking is not a calculation, it is a conceptualization. And it is a fairly natural one. Equal groups appear everywhere: eggs in egg cartons, crayons in boxes, or arrays of windows on the side of a building. The array is a natural way to arrange equal groups, and leads to all sorts of useful facts about multiplication. For example, I can see a $5 \times 7$ array as 5 rows of 7 or as 7 columns of 5 objects.

Thus 5 groups of 7 is 7 groups of 5, so $5 \times 7 = 7 \times 5$. This is not at all obvious with repeated addition. It’s not easy to see why 7 + 7 + 7 + 7 + 7 = 5 + 5 + 5 + 5 + 5 + 5 + 5. Of course, doing some calculation will show you that is true. But it won’t show you why it is true.
The equal groups way of thinking about multiplication clarifies the role of repeated addition. Starting in kindergarten, students understand addition as putting together; $2 + 3$ is the number of things you get when you put a set of 2 things together with a set of 3 things. When they understand multiplication in terms of equal groups, they can call on their prior understanding of addition and put all the groups together. Starting with $5 \times 7$ as the number of things in 5 groups of 7 things each, I can put the 5 groups together and get $7 + 7 + 7 + 7 + 7$. Note also that the equal groups way of thinking also copes quite nicely with $0 \times 7$. If I have 0 groups of 7 I don’t have anything at all, so $0 \times 7 = 0$.
Perhaps the most profound advantage of the equal groups way of thinking is that it can be extended to fraction multiplication. If I want to understand $\frac53 \times 7$, repeated addition is no help. What does it mean to add 7 to itself $\frac53$ times? On the other hand, you can make sense of $\frac53$ groups of 7. You have to work at it a bit; you have to decide what “$\frac13$ groups” means. But students in grade 2 used “one third of” for partitions of circles and rectangles, so it is not unnatural to suggest that “$\frac13$ groups” is one part of a group when you divide the group into 3 equal parts. A progression of representations leads from equal groups, for multiplication of whole numbers, to arrays, to area representations of multiplication that can be used for multiplying fractions:
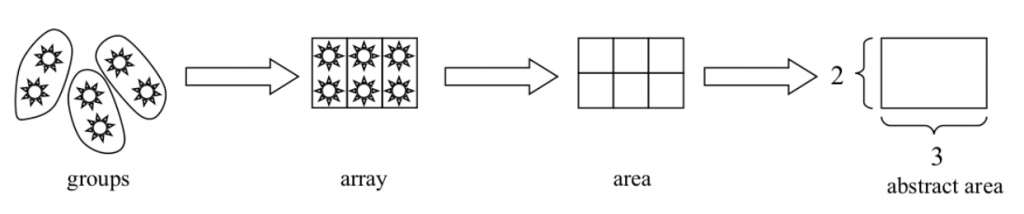
Multiplication does not need to be vexation. A clear conceptual picture of what multiplication is can help students to navigate the various strategies for carrying it out, and to recognize situations in which multiplication can be used to solve a problem.
Next Step
For a more extended discussion of the progression of representations, see Kristin Umland’s paper “The Role of Models in Mathematics Teaching and Learning.” (Note that the paper uses the word model for what I have called representations here.)
