Q: What is the fastest way to get a heated debate going about some topic in the IM 6–-8 math curriculum?
A: Show people this graph from Lesson 4 in Unit 8.5:

By Kristin Umland
Many of us learned that time is always the independent variable, and should therefore always be on the horizontal axis. This is a really powerful heuristic that we sometimes pass on to our students when they are learning about relations and functions. The problem is, it isn’t true.
How to Know the Role of the Variables
Why would we ever want to consider time as the dependent variable? David Butler (@DavidKButlerUoA) had a nice way of thinking about the example above:
For me the key has always been to focus not on the x-axis but on the y-axis. The thing on the y-axis is the thing you want to predict in your story. In this story, it seems Kiran wants to predict how long a run will take based on knowing how far it is.
In general, a context that involves a relationship between two quantities does not dictate which quantity is the independent variable and which is the dependent variable: that is a choice made by the modeler. Consider this situation:
A runner is traveling 1 mile every 10 minutes.
There is more than one way to represent this situation with a function.
- We can say the number of miles traveled, d, is a function of the number of minutes that have passed, t, and write d = 0.1t.
- We can also say that the number of minutes that have passed, t, is a function of the number of miles traveled, d, and write t = 10d.
These are both linear functions. The slope in the first corresponds to speed (0.1 miles per minute), and the slope of the second corresponds to pace (10 minutes per mile). Both have meaning, and both could be of interest. It is up to the modeler to decide what kinds of questions she wants to answer about the context and which function will be most useful in answering those questions.
There are also many instances in the scientific literature where time is a function of some other variable. A paper titled “Experimental Comparative Studies of Injection Systems” has this graph:
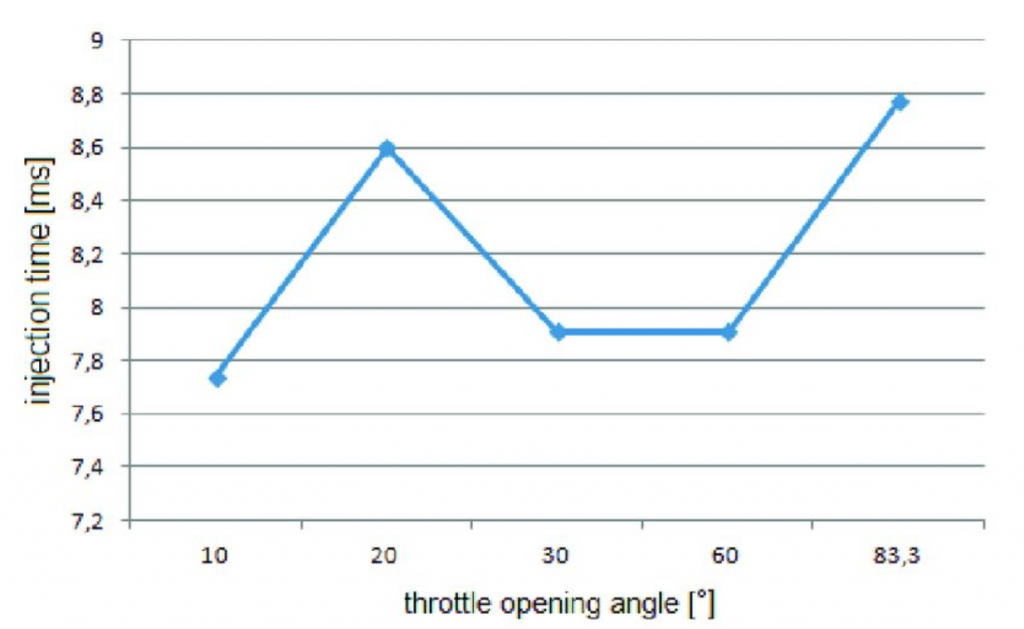
The authors (who are the modelers in this situation) chose to investigate how the injection time depends on the throttle opening angle.
Time and Time Again
The variables we call “time” take on two distinct flavors: (1) points in time (e.g. what is happening moment by moment) and (2) elapsed time (e.g. how long an event takes). When we think of a function abstracted from any particular context, the language we use to talk about the independent variable sounds very much like they are points in time. For example, we might ask “When is the function increasing?” when we want to know “For which values on the horizontal axis is the function increasing?”
I have a hunch that this way of thinking about functions in general is one of the reasons that it feels like time should always be on the horizontal axis. Interestingly, when we are considering time to be the dependent variable, it is often elapsed time, as it is in the contexts of the runner and the injection systems above. But it doesn’t have to be! Consider this situation:
It takes about 1 hour and 40 minutes for the New Mexico Rail Runner to travel from Albuquerque to Santa Fe. So the time that the train arrives in Santa Fe Depends on the time it departs Albuquerque.
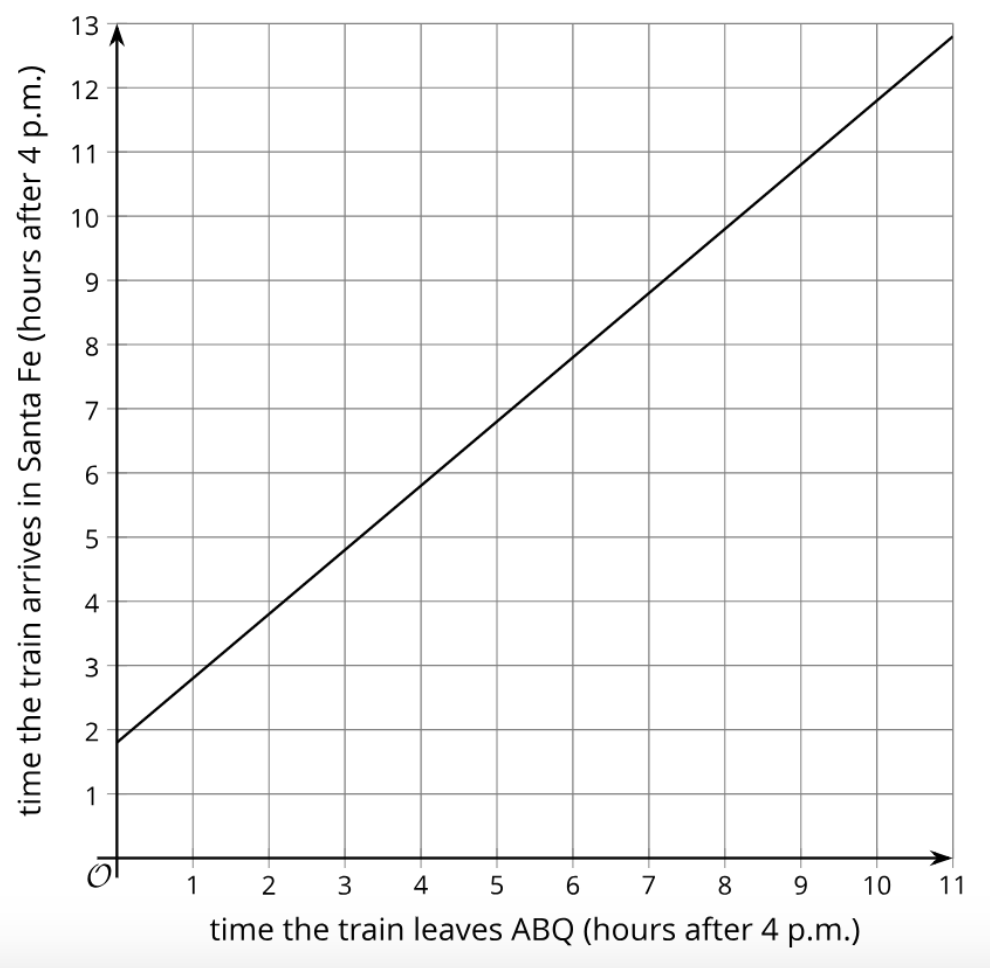
We can also think of it the other way around:
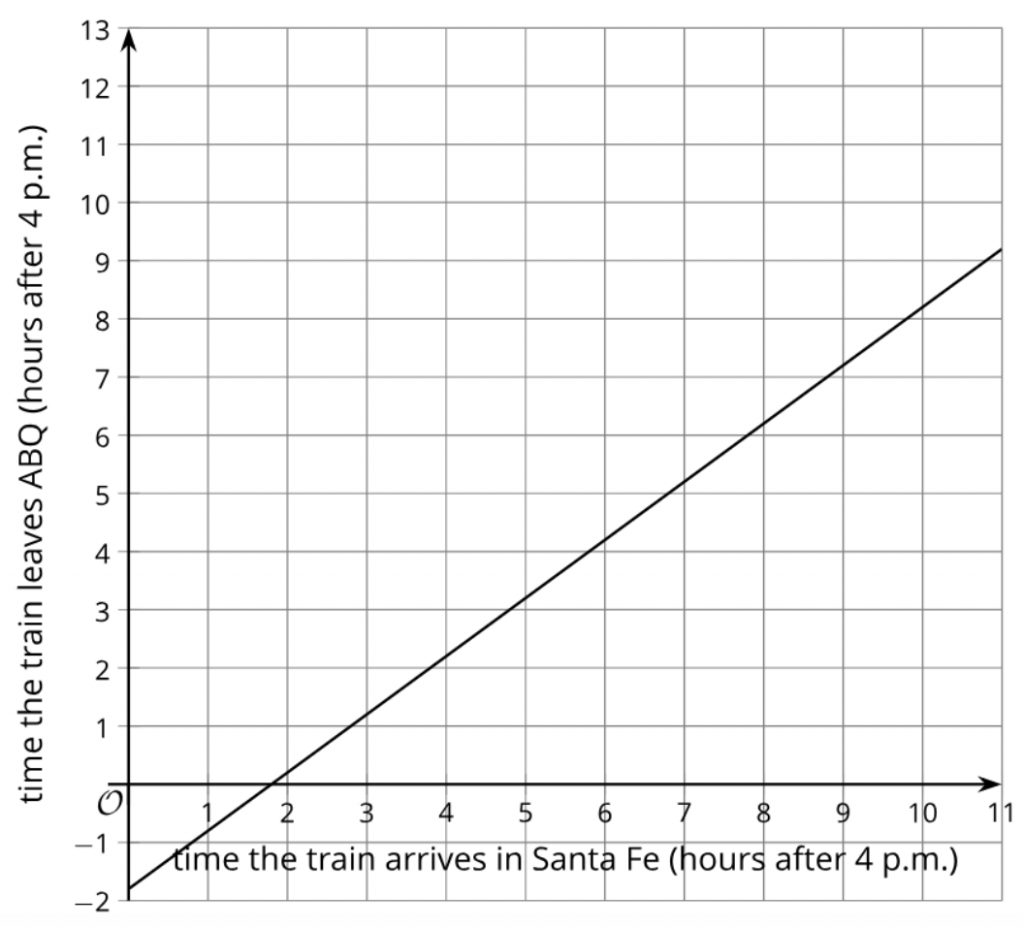
This feels uncomfortable to some people because time only moves forward, so how can something in the past depend on something in the future? It is sometimes challenging to figure out how the wording that describes the relationship between quantities changes when we switch the roles of the independent and dependent variables. But in this case, it is very natural to say, “The time that you should leave Albuquerque depends on the time you want to arrive in Santa Fe.”
Thinking about Functions in General
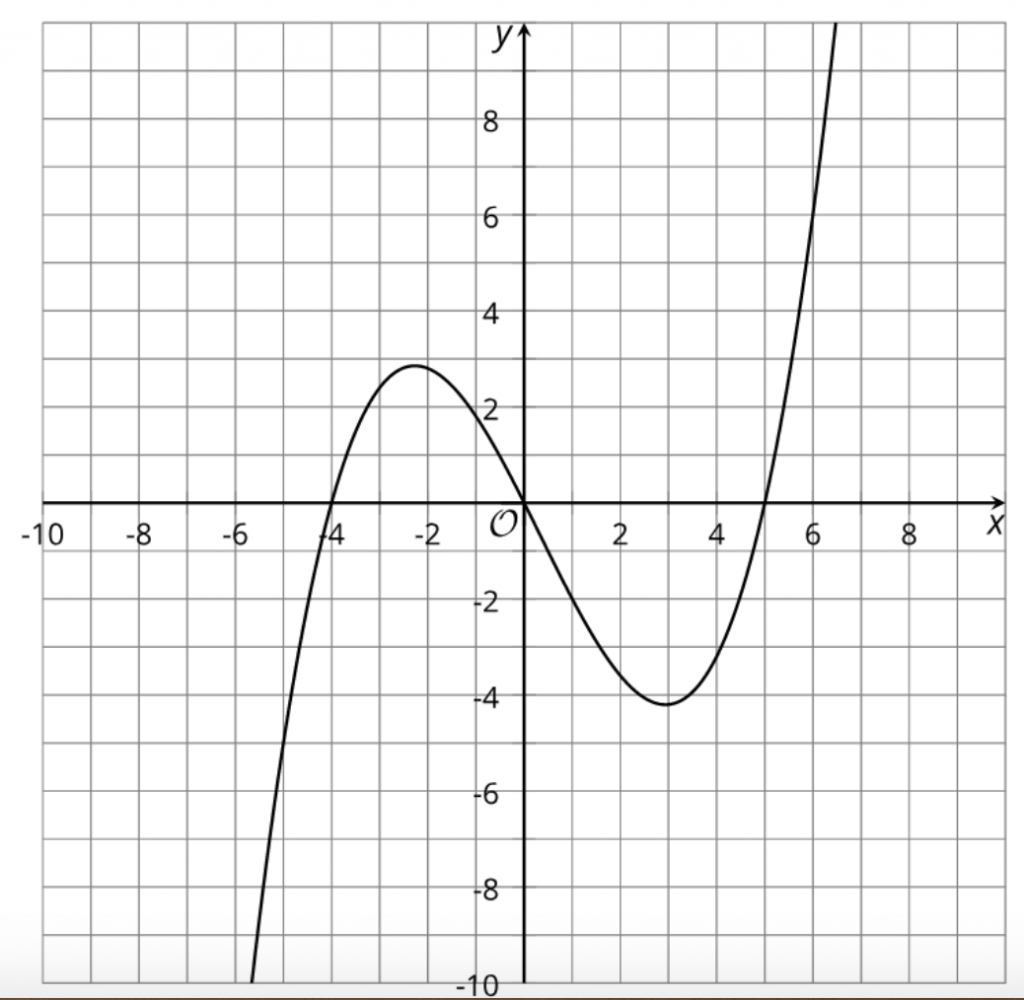
In general, when we have a relationship between two quantities A and B, we can always ask, “Is quantity A a function of quantity B? Is quantity B a function of quantity A?” Consider an equation like

When we have a well-defined relationship between two quantities, we can always ask the question: “Which of these quantities can be viewed as a function of the other?” The challenge often comes in making sense of what it would mean in each case for a given context.
Next Step
Can you think of any other interesting contexts where it would be appropriate to think of time as a function of a different quantity than the examples given here?
