By Kate Nowak
When I was teaching high school mathematics, my local colleagues and I spent a whole lot of time creating problem-based lessons. We were convinced that this style of instruction was a good way to learn, but the textbooks in use at our school simply contained definitions and theorems, worked examples, and practice problems. One day I was talking to my dad about how much time I had been spending lesson planning. His response was, “People have been teaching geometry for, what, 3,000 years? Shouldn’t the lessons be, like, already planned?”
To be fair, comprehensive problem-based materials existed at the time, but we didn’t have access to them, and materials that were really aligned to our new state standards weren’t available. We did a good job, but if we’d already had the sort of materials we were building, we could have used the time to improve our teachercraft (like giving frequent feedback, questioning strategies, or helping students improve their discourse). So when I was offered an opportunity to come to Illustrative Mathematics and start work on a grades 6–8 curriculum that would be released as an open educational resource, I jumped at the chance to create materials like the ones I wish we’d had. (They’re actually way better than I could have imagined, due to the expertise of the writing team and all the collaborators and our culture of savage and good-natured criticism.)
IM started as a website providing tasks to help teachers, curriculum developers, and other members of the public better understand the standards. Why did we decide to write a complete curriculum? IM’s mission is to create a world where learners know, use, and enjoy mathematics. Recent research tells us that curriculum is a critical factor in academic success, and that many students have insufficient opportunity to access grade-level mathematics. Making high-quality curriculum aligned to national and state standards available to as many schools, teachers, and learners as possible is an important way we work toward our mission.
In the time since we decided to embark on curriculum work, we developed a 6–8 curriculum that earned rave reviews and is in its second year of widespread use. For the past year and a half, we’ve been hard at work on a curriculum addressing high school standards. Our first draft is being piloted in 56 schools across the United States, and our ongoing collaboration with our cohort of thoughtful, generous, eagle-eyed pilot teachers is informing revisions to these pilot materials. Version 1 will be released in summer of 2019, and you can see unit 1 of each course here. This post is a sneak peek to accompany a webinar we offered a few weeks ago. Pretty soon, our trailer will drop. Just kidding. Wouldn’t it be cool if math curricula had trailers? But we did make a playlist.
This post will address some features that IM Algebra 1, Geometry, Algebra 2 has in common with IM 6–8 and also some new features unique to high school.
First of all, what are we making?
- Three Courses: Algebra 1, Geometry, Algebra 2 and associated teacher professional learning
- Extra Support Materials for Algebra 1
- Addressing the non-(+) Common Core State Standards
It was important to us to create a set of materials that, when implemented well by skilled educators, would prepare every student to be successful in an introductory college math course. Our development team is looking forward to creating materials that can be used in more contexts in the future (for example, an integrated sequence, an accelerated middle school option so that Algebra 1 is completed by the end of middle school, and coursework addressing (+) standards).
Here are the unit titles in the three courses:
Notice the extra support materials running parallel to the Algebra 1 course. I’ll describe those in further detail in a minute. Also, if you’re wondering where modeling fits in here, stay tuned for a few paragraphs.
There is some flexibility to rearrange units to meet local needs. This dependency map shows how to preserve coherence.
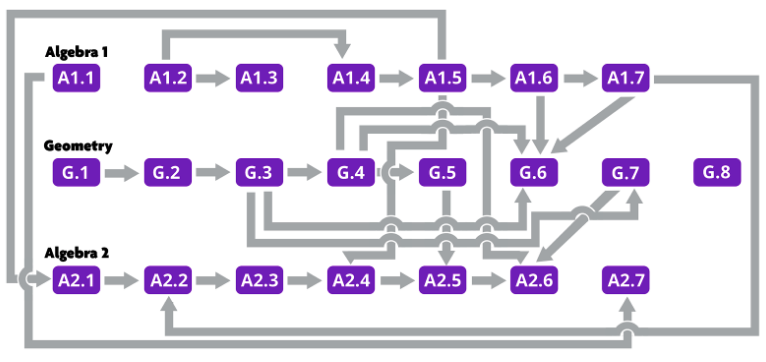
If no modifications are made, students would encounter Algebra 1 then Geometry then Algebra 2, progressing through each unit from left to right through each course. Where there is an arrow, the later unit depends on knowing some stuff from the previous unit. For example, G.7 is Circles, and there is an arrow from G.7 pointing to A2.6, Trigonometric Functions. If units are rearranged, just make sure the arrows stay in the forward direction.
I want to address three important features this new curriculum has in common with IM 6–8. It is:
- problem-based
- iteratively structured
- designed to be accessible to all students
Problem-based means that the curriculum is designed to make it possible for students to spend most of their time in math class doing mathematics. In other words, they have a chance to figure some stuff out before you tell them what to do.
From Bill’s recent blog post:
The National Academies publication How People Learn shows that student learning is more robust if students first have a chance to grapple with a problem before hearing explicit instruction on it. Both components, and the order in which they happen, are important. (See, for example, the box on page 59.) Students also may need guidance in understanding what the problem is asking, without being told how to solve it.
Problem-based instruction means believing all students can solve problems on their own and giving them a chance to try. The curriculum we write is designed to support problem-based instruction. Each lesson is built around a set of activities that students can work on by themselves or in groups, starting with a warm-up that activates relevant prior learning. The activities are designed to be amenable to different approaches that different students might bring to the work. Because not all students will be ready just to jump right in, each activity has a launch which is designed to help them understand the problem without giving away the punchline. Each activity also has a synthesis at the end where the teacher makes sure that each student has learned the mathematics the activity was designed to teach.
Iteratively-structured means that each unit, lesson, and activity loosely follows a predictable structure. This representation shows the different zoom levels where this structure is evident:
A lesson is designed for use by a teacher interacting in person with a group of students. Each lesson is meant to take 45–50 minutes, although can take longer depending on choices made by the teacher. The schools piloting the materials this year use a variety of creative bell schedules, about half of which could be characterized as a “block schedule” featuring class meetings that are longer than 45–50 minutes, but meet less frequently than every day. Guidance for adapting these materials for some different types of schedules is on our development roadmap.
Designed to be accessible to all students means that we assume every student can and should access grade-level mathematics. Activities are designed to maximize the chances that all students can participate, and additional supports are provided for teachers of students with disabilities and teachers of English language learners.
As the high school curriculum began to take shape, we allowed everything we learned and the thinking that went into the middle school curriculum to inform what we were building. But we realized that there were some additional things the high school curriculum needed to do.
New features in the high school curriculum:
- approach to digital tools
- mathematical modeling prompts
- extra support materials for Algebra 1
Approach to digital tools: The middle school curriculum has a digital version of the student materials that includes embedded, dynamic applets customized to the activity (here’s an example). High school students should be learning to use available tools to create representations to help them understand or solve problems. So, the high school curriculum includes far fewer custom applets. Instead, it includes activities whose purpose is to teach students how to use tools that are available to them. And then in later activities where using a tool strategically is a good option, the lesson plan signals to the teacher that this is the case.
The teacher materials describe how to use the dynamic tools within the platform, but the student materials are as platform-agnostic as possible, so that a teacher could substitute instruction on a different tool if needed. The digital version of the student materials features a “Math Tools” button that is accessible from every page. See this student page, for example. The “Math Tools” button is in the upper right.
Mathematical modeling prompts: We found that our middle school structure of classroom lessons and activities didn’t allow us to address the full scope of mathematical modeling needed at the high school level. So, we’ve created a new type of thing called a mathematical modeling prompt. This can be thought of as a project or simply an assignment. It is meant to be launched in class by a teacher, but then students can work on it independently or in small groups in or out of class. It can be thought of as a similar type of assignment as a paper in an English class, where the class continues to use class time to progress through lessons, but students are working on the prompt outside of class with intermediate due dates. We built in maximum flexibility for a teacher to implement these in a way that will work for them.
Just to be clear, students are still doing aspects of modeling within the regular lessons. It’s just that we needed this new type of component to offer a way for students to engage in the complete modeling cycle, including potentially time-consuming endeavors like refining the question, conducting research or simulations, iterating on their model, and reporting their findings. Check out some examples of modeling prompts in the Geometry course, and read more about them in the course guide.
Extra support materials for Algebra 1: In the United States, many students struggle to pass Algebra 1, and this leads to adverse outcomes. Most schools offer additional time in a student’s schedule to support their success in Algebra 1. However, teachers who are tasked with planning what to do with this time are often stuck generating materials. As part of version 1 of this curriculum, we are also providing extra support materials for Algebra 1.
We researched the latest thinking about best practices on how to support these students, and the structure of these materials reflects the outcome of that research. The extra support materials give students opportunities to access grade-level mathematics in age-appropriate contexts. They do not delay Algebra 1 content, and invite students to reason mathematically and communicate their thinking at the same level of rigor as the Algebra 1 course.
The support materials are each structured the same way: a warm-up that addresses numeracy and sense-making, a portion where students learn or revisit content, and a portion where students can practice independently or in pairs.
Every Algebra 1 lesson has associated support materials. The support materials are meant to be encountered by students before they engage in the corresponding Algebra 1 lesson. The purpose of the extra support materials is to make it more possible for students to engage in grade-level content.
For example, here’s an activity from Algebra 1, Unit 7:
And here’s an activity from the associated extra support materials, meant to prepare students to be more successful with that activity:
The extra support materials aren’t visible on the preview site yet, since development has necessarily lagged behind the Algebra 1 course. With the release of version 1 this summer, nearly every Algebra 1 lesson will have associated support materials (with a few exceptions).
Note that the support materials aren’t a complete course—they don’t contain everything our other courses do. For example, they don’t have their own assessments or practice problems. They are classroom materials for use during additional scheduled class time.
Here are some other interesting facts about our process: Over 60% of the high school writing team was also part of developing the middle school curriculum. We got to take everything we learned from that experience to inform the creation of the high school materials. 75% of our writing team is composed of current and former 6–12 teachers. 17% are current classroom teachers. (The others are mathematicians and mathematics education researchers.)
From hundreds of interested schools that applied, our pilot schools were chosen to ensure we were piloting the materials with as diverse a student and teacher population as possible. Pilot teachers are invited to give input on the materials through a comprehensive suite of surveys. Additionally, our writing team visits pilot sites, and our professional learning facilitators interact with pilot teachers regularly. All of these open avenues for communication inform the development on a daily basis.
So, are you excited? I’m excited! Look for the full release of IM Algebra 1, Geometry, Algebra 2 in summer of 2019. And then look forward to K–5, piloting in 2020-2021 and rolling out for all in 2021-2022! IM K–12 is coming for you, current 3-year-olds!
Next Steps
- Watch the webinar, if you prefer to hear this information. (Scroll down a bit on this page.)
- Check out our A’s to the webinar participants’ Q’s.
- Peruse unit 1 of each course.
- Interested in considering adopting for your school or district? Learn more about our IM Certified curriculum distribution partners.
