By Kristin Umland,VP Content Development
A great conversation I had with the IM elementary school curriculum writing team got me thinking: What is a measurable attribute? That is, when given an object, what can we measure about it? Before you jump in with your own answer, consider these questions:
Is “redness” a measurable attribute? Why or why not? Does this picture help you decide?
One criterion for an attribute to be measurable is that you can ask these kinds of questions:
“Which of these two objects is bigger/greater/more [blank] than the other?”
If an attribute is measurable, you can compare two things along that dimension using this kind of language. But clearly, this isn’t enough. “Which of my two uncles is [funnier] than the other” doesn’t have an objective answer. My friend laughs at fart jokes, and says Uncle Alonso is funnier. But her brother prefers knock-knock jokes, and says Uncle Beto is funnier.
So a measurable attribute needs to have a well-defined scale that is in common use, where independent measurers can each produce a numerical measurement and will agree on the value of that measurement.
Definitely measurable:
- Longness
- Heaviness
- Voluminousness
Not so sure:
- Sweetness
- Redness
- Hardness
Probably not measurable:?
- Stinkiness
- Crinkliness
- Loveliness
The reason this all came up is that we were thinking together about this standard:
K.MD.A.1 Describe measurable attributes of objects, such as length or weight. Describe several measurable attributes of a single object.
Let’s answer a question that might be easier to address than trying to characterize measurable attributes in general:
“What measurable attributes should students be describing in kindergarten?”
Reading the grade-level overviews in the standards and the measurement progressions document, it is much clearer what the focus of the MD standards should be in elementary school across K-5: length, area, and volume. The measurement progression document suggests that kindergarteners might explore all of these attributes, keeping in mind that kindergarteners will not learn about these attributes in a formal way until later grades: measuring length comes in grade 1, area in grade 3, and volume in grade 5. Kindergarteners should definitely be able compare two objects of different lengths and identify which is longer. Even though we thought of ways to address area appropriately at this level, we decided not to include it as a major focus in kindergarten. We also decided not to address the general notion of volume, but instead focus on capacity, which is much more accessible to kindergarteners. The standard also mentions weight.
Are there any other attributes that should be included?
- Kindergarteners could potentially compare the duration of time intervals, but this is pretty abstract (that is, not perceptible by visual inspection or physical interaction) and they don’t begin their study of time until grade 1.
- The speed of an object moving at constant speed could be considered a measurable attribute, but constant speed isn’t introduced until grade 6 when students first study rates.
- Density is a measurable attribute, but students don’t have the tools to study it until grade 7 when they study proportional relationships.
We decided to stick with length, weight, and capacity as the primary focus of this work.
It turns out that people are very creative in inventing measurement systems for all kinds of attributes, but many of these measurement systems are too abstract for kindergarteners. The color scales in the first image provide an example of how we can measure “redness” (at least for digital images). People measure sweetness on a “percent sucrose equivalent” scale, and hardness can be measured using either Vickers hardness scale or Mohs’ scale. One very important aspect of many of these scales is that they are represented using an understanding of length via a mapping to the number line, like the redness scale above, or like a thermometer that measures temperature. Another example is the decibel scale for loudness:
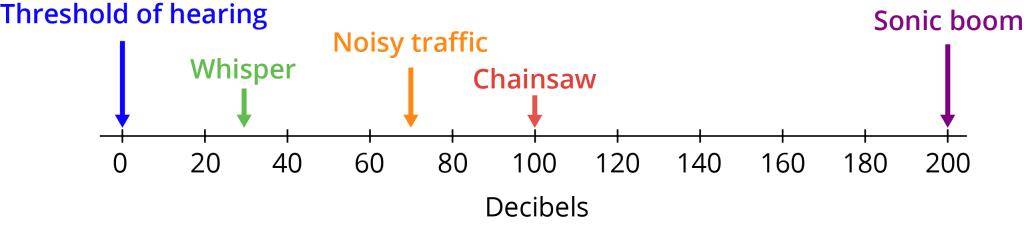
As students learn more and more over time about measurement, they build on their understanding of length to understand measurable attributes that are more abstract than that. The important work on understanding geometric measurement that starts in kindergarten and continues through high school is key to understanding any measurement system that humans might devise.
Next Steps
What are some other measurable attributes you can think of, and what would students need to know in order to understand the measurement scale we use to measure them? Can you imagine a new measurement system for some attribute that has not yet been devised?
