By Vanessa Cerrahoglu, Jennifer Wilson, and Liz Ramirez
We envision creating a world where learners know, use, and enjoy mathematics. Knowing and using math goes beyond calculating and evaluating. We create purposeful opportunities for students to engage in sense-making and use language to negotiate meaning with their peers. This calls for a language-rich environment where there’s space for all students to participate in argumentation and explanation.
What do these conversations look like now that we are no longer sharing physical space together? And how do we support our multilingual students who are gaining proficiency with English?
In this series of posts, we continue to consider how to “strengthen the opportunities and supports for helping students to describe clearly their mathematical thinking to others, orally, visually, and in writing” by looking at three Math Language Routines (MLRs). The posts in the series have been about enhancing access, MLR 3 (Clarify, Critique, Connect), and MLR 5 (Co-Craft Questions). You can learn more about the MLRs here.
In this post we will explore MLR 7 Compare and Connect.
MLR 7 Compare and Connect
In the Compare and Connect routine (MLR 7), students make sense of mathematical strategies by relating and connecting other approaches to their own. This routine can be used to support discourse around a problem that can be approached and solved using multiple strategies or representations. Let’s explore this routine through the lens of the following activity from Algebra 1 Unit 4 Lesson 18.

As they solve the prompt, students will have to make assumptions about the context in order to model it. The goal of the discussion will be making these assumptions visible. We look to the structure of this routine to prepare students to engage in a conversation centered on making connections and comparing approaches in order to recognize the role assumptions play in reaching a mathematical solution. Students will prepare displays of their work, compare their reasoning with the reasoning of others, and use language to connect the representations.
Here is the support for English Language Learners provided for this activity.
| Support for English Language Learners Representing, Conversing: MLR7 Compare and Connect. Use this routine to prepare students for the whole-class discussion. At the appropriate time, invite students to create a visual display showing their strategy and calculations. Allow students time to quietly circulate and analyze the work in at least 2 other displays in the room. Give students quiet think time to consider how the solution strategies are alike and how they are different. Next, ask students to find a partner to discuss what they noticed. Listen for and amplify observations that highlight the assumptions and choices that were made in each display. This will help students understand how variations in assumptions and choices may lead to different predictions and solution strategies. Design Principle(s): Optimize output; Cultivate conversation |
What might this look like during distance learning?
Here’s how it happened recently with a group of Algebra I students in Duarte, CA.
First, students prepared displays of their work, showing how they made sense of the problem and why their solution makes sense. Some opted to use the tools of the video conferencing application while others chose to use paper and pencil.
Compare
During a synchronous video meeting, students examined each others’ work. It turned out that two students, Eduardo and Nuri, had a similar approach.
Eduardo exclaimed “Nuri did it like me!” The teacher pushed: “Can you say more? How can you tell that you both had a similar approach?”
As Eduardo explained, he highlighted pieces on Nuri’s work that were similar to his.

“Nuri and I both showed the numbers 10, 20, and 10 along the side.”
“What do those numbers represent?” the teacher asked.
“The change in the time,” Eduardo continued. “It’s 10 minutes to get from 11:00 to 11:10, and 20 minutes to get from 11:10 to 11:30.”
Eduardo also highlighted the equation $9 + 20 + 8 = 37$. “That’s the change in the percent charged. It went up $9 + 20 + 8$ or 37% in the 40 minutes from 11:00 to 11:40.”
The teacher paused. “Nuri, where is your work different from Eduardo’s?” The conversation continued with evidence from the student work.
Connect
Students looked for similarities and differences. Eduardo noticed that everyone tracked the change in percent charged—9, 20, 8. But there was something in Ameilia’s work that puzzled her classmates.
Ameilia’s Work
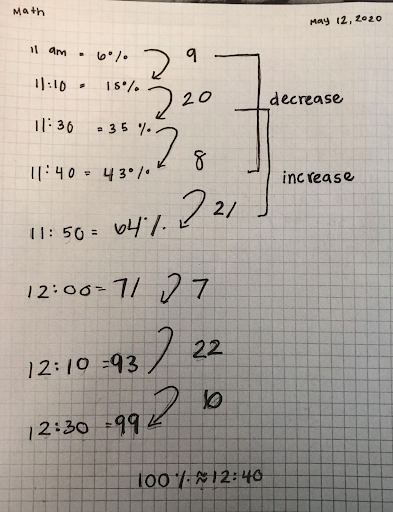
What puzzled the group was Ameilia’s sequence of: 9, 20, 8, 21, 7, 22,. . . This prompted Eduardo to ask, “How did you get 21, 7 and 22?” Ameilia described she noticed a downward trend in the nine and eight (9, 20, 8, …) and assumed an upward trend in the other numbers (9, 20, 8, 21, 7, 22…), “I followed the patterns,” she shared.
A collective, “ah!” could be heard by the group at this point.
Asynchronous Learning
In asynchronous settings, students should submit an image of their work, whether it’s a screen capture or a photo of paper and pencil work. The teacher then selects and prepares student work samples to focus the “compare” and “connect” conversation using a discussion board or shared electronic document.
Why use this routine?
Let’s go back to our question: What happens when we pay attention to language?
By focusing on language, the teacher created an opportunity for students to go beyond just describing their own process and answer. Students explored connections between their thinking and the thinking of others. Students used oral language to reflect on their reasoning, and comparisons between their work and the work of others. This allowed them to encode their thinking in a different way than just numerically or visually. Just as students benefit from examining multiple mathematical diagrams, linking these different language representations (oral, representational) increases sensemaking and also makes the learning stickier.
When students were asked about a new insight gained from the conversation, Eduardo said, ”a new insight I have is that everyone has a different style of thinking and how they solve problems. A lot of people have different ways of solving a problem so it’s cool to see how other people do their problems to get an answer.”
Special thanks to Ann Kim and her students for sharing their learning with us.
Next Steps
Here’s an activity from each grade level that makes use of the Compare and Connect routine.
- Grade 6 Unit 4 Lesson 11 Activity 3: Using an Algorithm to Divide Fractions
- Grade 7 Unit 5 Lesson 16 Activity 4: Equations Tell a Story
- Grade 8 Unit 3 Lesson 4 Activity 2: Comparing Two Different Representations
- Algebra 1 Unit 4 Lesson 8 Activity 2: Flag Raising (Part 2)
- Geometry Unit 1 Lesson 18 Activity 3: Point by Point
- Algebra 2 Unit 2 Lesson 9 Activity 2: The Case of Unexpected End Behavior
We would love to learn alongside you. How have you used MLR 7 with your students during distance learning? Share your Compare and Connect prompt, and, if possible, student work, at #LearnWithIM.
