By Zack Hill
The major work of grade 3 includes representing and solving problems that involve multiplication and division. Then, by the end of grade 3, students are expected to know from memory all products of two one-digit numbers. What does this look like and how do we accomplish it?
3.OA.C.7
Fluently multiply and divide within 100, using strategies such as the relationship between multiplication and division (for example, knowing that 8 × 5 = 40, one knows 40 ÷ 5 = 8) or properties of operations. By the end of Grade 3, know from memory all products of two one-digit numbers.
When I came on as the grade 3 lead writer for the IM K–5 curriculum, I was very much aware of the phrase in 3.OA.C.7 that reads, “By the end of grade 3. . . .” I was excited to explore what it would mean to enact this phrase in a curriculum in a way that would serve every student.
As an instructional coach, I spent time working with teachers around this standard and was excited for the opportunity to work on building a curriculum where fluency unfolded deliberately throughout the year. As we considered the design principles and began writing, several approaches emerged:
- targeted unit work that builds a conceptual foundation for the operations
- year-long trajectory of instructional routines
- activities, centers, and practice problems to practice the operations
- final unit on grade-level fluency
Targeted unit work that builds a conceptual foundation for the operations.
Early units in grade 3 establish a strong foundation of conceptual understanding of multiplication. Multiplication is introduced in the first unit with the concept of equal groups. Students match representations to story situations, and record multiplication expressions. For example, students write an expression to represent this diagram.
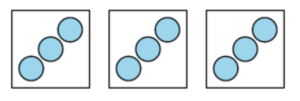
It was also important to note what we didn’t ask students to do. We did not ask them to find the total number of objects until the fourth lesson on multiplication. It was important to carve out time for students to make sense of the meaning of multiplication before asking them to find the value of products.
Later units built off this conceptual understanding of multiplication as equal groups. After exploring multiplication in the context of scaled bar graphs and picture graphs, students look for equal groups in the structure of arrays and relate arrays to multiplication. This leads students into Unit 2 where they relate the structure of rectangular areas to multiplication. In Unit 3, as students wrap up their work adding and subtracting within 1,000, they learn how 2-step problems can involve multiplication, as well as addition and subtraction. In Unit 4, students learn about division and how it’s related to multiplication. They dive deep into how strategies that are based on properties of operations and the relationship between multiplication and division can be used to multiply and divide larger numbers. Visual representations are used to support students in making sense of strategies and representing the strategies more abstractly.

Year-long trajectory of instructional routines
Instructional routines are designed to be invitational to students. Students have the opportunity to engage in routines like Notice and Wonder and How Many Do You See? with images like the one below before they are asked to compute the value of a product.
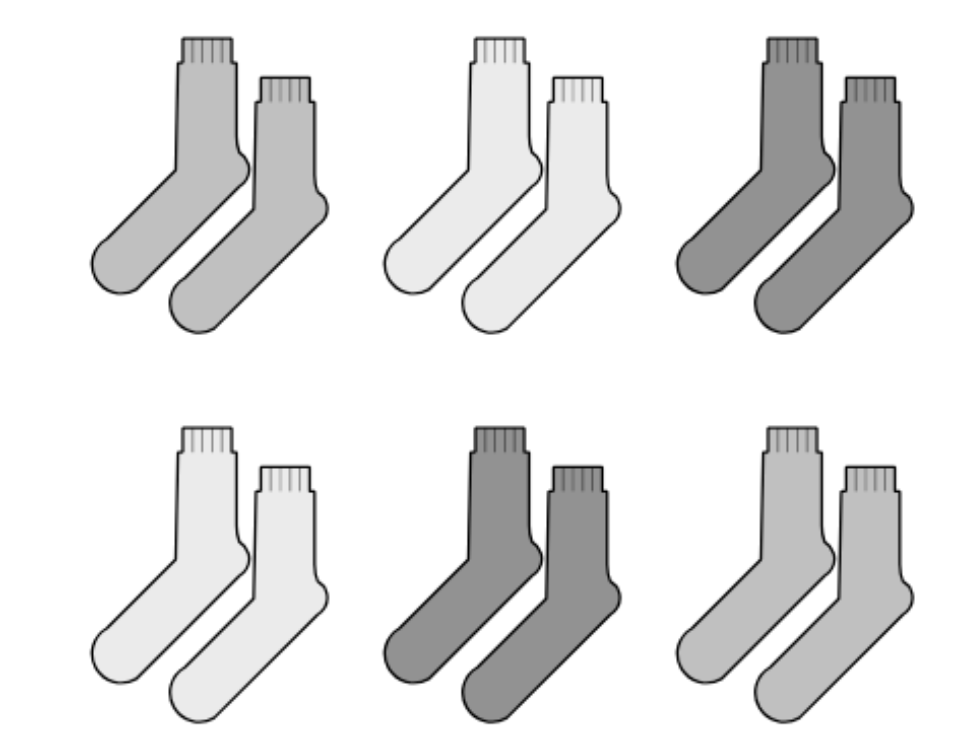
This communicated that there was value, not just in finding how many objects were in a set of equal groups, but in seeing equal groups in different ways and asking good questions about equal groups.
In every unit, students have opportunities to develop fluency with number talks that build on previous work. Early number talks support the conceptual understanding of multiplication. In the number talk on the left, students have the opportunity to notice that the product increases by 5 because each expression is adding one more group of 5. Later number talks similar to the one on the right give students opportunities to find more challenging products by applying these same ideas about the number of groups, using a product like 5 x 7 to find 4 x 7 or 6 x 7 by adding or subtracting a group of 7.

Activities, centers, and practice problems to practice the operations
Students’ work with multiplication and division doesn’t stop after Unit 4. Students continue to work towards fluency through opportunities to apply their work with multiplication and division to problems that involve liquid volume and mass in Unit 6, and working with perimeter and area in Unit 7.
Centers are suggested in each lesson and provide another opportunity for students to practice using strategies they’ve learned throughout the year in a way that’s engaging and aligned to grade-level standards. One center that is used throughout the year is Rectangle Rumble. In this center, students generate two numbers, then draw and shade a rectangle with these side lengths on a grid. The goal is to fill the grid with the most rectangles, so students find the number in each rectangle as they go, then find the total number of rectangles once the grid is full. There are three stages that students can use throughout the year. Stage 1 only includes factors of 1, 2, 5, and 10. Stage 2 includes factors of 1–5. Stage 3 includes factors 1–10. The idea is that the center can grow with students as their familiarity and experience with multiplication grows throughout the year.
Final unit on grade-level fluency
In the final unit, students revisit major work of the grade. There are opportunities to revisit the application of multiplication to area as students participate in lessons themed around design. There is also a section on multiplication and division where students play games and work on centers to continue to develop or demonstrate fluency.
All of these design considerations contribute to a grade 3 curriculum that doesn’t confine fluency to a single unit, but provides many opportunities for students to build towards fluent multiplication and division within 100 throughout the year. Students know their single digit multiplication facts from memory because they have a year’s progression of meaningful activities to draw from.
Next Steps
Consider how multiplication is introduced to students. Do they have ample time to make sense of the meaning of multiplication and division before they are asked to find the value of products and quotients?
Look for opportunities to build toward fluent multiplication and division throughout the year that leverage what students know.

