By Jennifer Willson, Director, 6–12 Professional Learning Design
In my role at IM, working with teachers and administrators, I am asked to help with the challenges of implementing an IM curriculum. One of the most common challenges is: how can we best align these materials to our homework and grading practices? This question is a bit different from “How should we assess student learning?” or “How should we use assessment to inform instruction?”
When we created the curriculum, we chose not to prescribe homework assignments or decide which student work should count as a graded event. This was deliberate—homework policies and grading practices are highly variable, localized, and values-driven shared understandings that evolve over time. For example, the curriculum needed to work for schools where nightly, graded assignments are expected; schools where no work done outside of class is graded; and schools who take a feedback-only approach for any formative work.
IM 6–8 Math was released in 2017, and IM Algebra 1, Geometry, and Algebra 2 in 2019. In that time, I’ve been able to observe some patterns in the ways schools and teachers align the materials to their local practices. So, while we’re still not going to tell you what to do, we’re now in a position to describe some trends and common ways in which schools and districts make use of the materials to meet their local constraints. Over the past four years, I have heard ideas from teachers, administrators, and IM certified facilitators. In December, I invited our IM community to respond to a survey to share grading and homework policies and practices. In this post I am sharing a compilation of results from the 31 teachers who responded to the survey, as well as ideas from conversations with teachers and IMCFs. We hope that you find some ideas here to inform and inspire your classroom.
How do teachers collect student responses?
Most teachers who responded to the survey collect student work for assessments in a digital platform such as LearnZillion, McGraw-Hill, ASSISTments, Edulastic, Desmos, etc. Others have students upload their work (photo, PDF, etc.) to a learning management system such as Canvas or Google classroom. Even fewer ask students to respond digitally to questions in their learning management system.
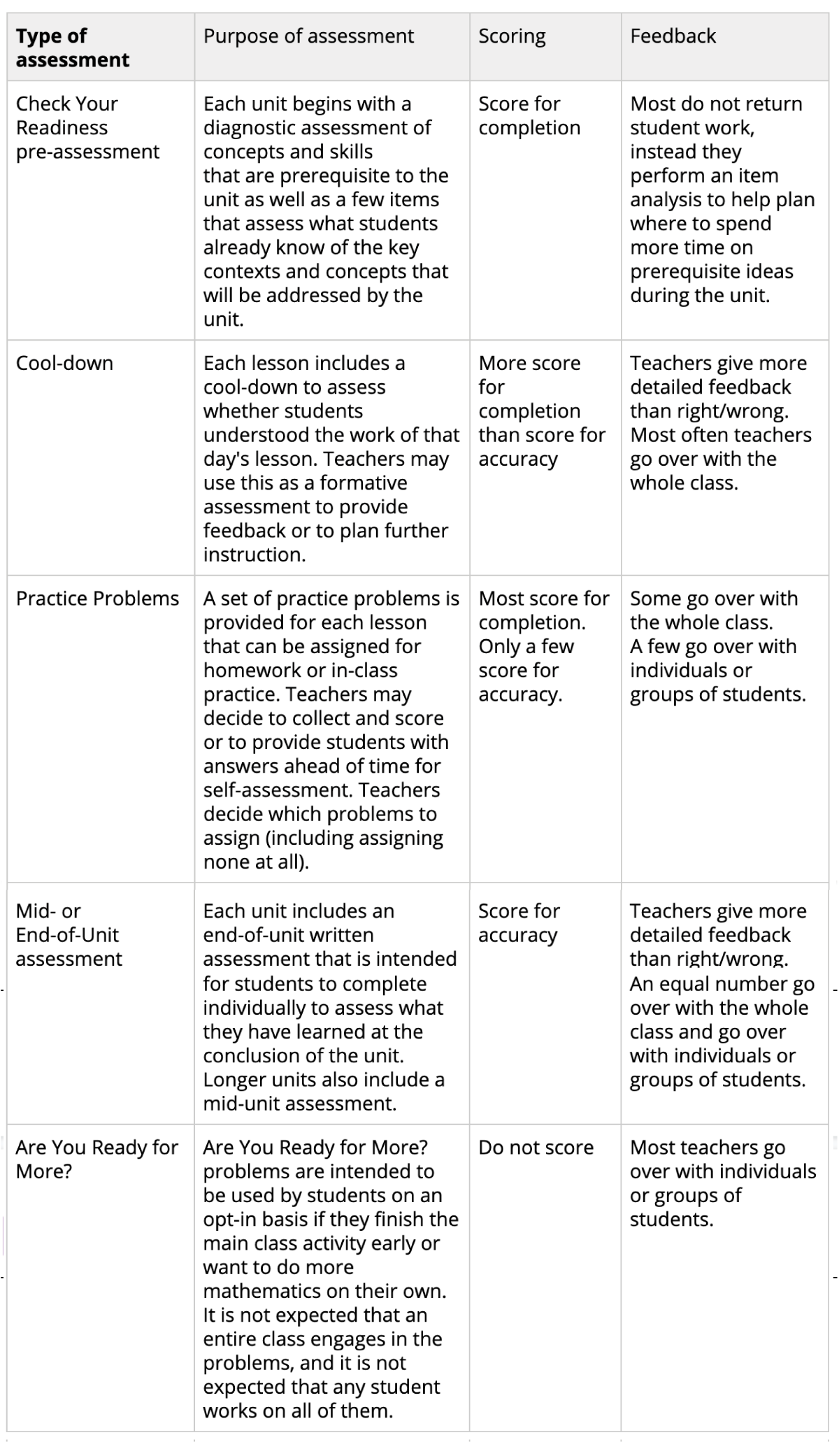
How do teachers tend to score each type of assessment, and how is feedback given?
The table shows a summary of how teachers who responded to the survey most often provide feedback for the types of assessments included in the curriculum.
How are practice problems used?
Every lesson in the curriculum (with a very small number of exceptions) includes a short set of cumulative practice problems. Each set could be used as an assignment done in class after the lesson or worked on outside of class, but teachers make use of these items in a variety of ways to meet their students’ learning needs.
While some teachers use the practice problems that are attached to each lesson as homework, others do not assign work outside of class. Here are some other purposes for which teachers use the practice problems:
- review
- extra practice
- student reflection
- quizzes
- as examples to discuss in class or use for a mini-lesson
- as a warm-up question to begin class
- as group work during class
How do teachers structure time and communication to “go over” practice problems?
It’s common practice to assemble practice problems into assignments that are worked on outside of class meeting time. Figuring out what works best for students to get feedback on practice problems while continuing to move students forward in their learning and work through the next lesson can be challenging.
Here are some ways teachers describe how they approach this need:
- We don’t have time to go over homework every day, but I do build in one class period per section to pause and look at some common errors in cool-downs and invite students to do some revisions where necessary, then I also invite students to look at select practice problems. I collect some practice problems along with cool-downs and use that data to inform what, if anything, I address with the whole class or with a small group.
- Students vote for one practice problem that they thought was challenging, and we spend less than five minutes to get them started. We don’t necessarily work through the whole problem.
- I post solutions to practice problems, sometimes with a video of my solution strategy, so that students can check their work.
- I assign practice problems, post answers, invite students to ask questions (they email me or let me know during the warm-up), and then give section quizzes that are closely aligned to the practice problems, which is teaching my students that asking questions is important.
- I invite students to vote on the most challenging problem and then rather than go over the practice problem I weave it into the current day’s lesson so that students recognize “that’s just like that practice problem!” What I find important is moving students to take responsibility to evaluate their own understanding of the practice problems and not depend on me (the teacher) or someone else to check them. Because my district requires evidence of a quiz and grade each week and I preferred to use my cool-downs formatively, I placed the four most highly requested class practice problems from the previous week on the quiz which I substituted for that day’s cool-down. That saved me quiz design time, there were no surprises for the students, and after about four weeks of consistency with this norm, the students quickly learned that they should not pass up their opportunity to study for the quiz by not only completing the 4–5 practice problems nightly during the week, but again, by reflecting on their own depth of understanding and being ready to give me focused feedback about their greatest struggle on a daily basis.
- I see the practice problems as an opportunity to allow students to go at different paces. It’s more work, but I include extension problems and answers to each practice problem with different strategies and misconceptions underneath. When students are in-person for class, they work independently or in pairs moving to the printed answer keys posted around the room for each problem. They initial under different prompts on the answer key (tried more than one strategy, used a DNL, used a table, made a mistake, used accurate units, used a strategy that’s not on here…) It gives the students and I more feedback when I collect the responses later and allows me to be more present with smaller groups while students take responsibility for checking their work. It also gets students up and moving around the room and normalizes multiple approaches as well as making mistakes as part of the problem solving process.
Quizzes—How often, and how are they made?
Most of the teachers give quizzes—a short graded assessment completed individually under more controlled conditions than other assignments. How often is as varied as the number of teachers who responded: one per unit, twice per unit, once a week, two times per week, 2–3 times per quarter.
If teachers don’t write quiz items themselves or with their team, the quiz items come from practice problems, activities, and adapted cool-downs.
When and how do students revise their work?
Policies for revising work are also as varied as the number of teachers who responded.
Here are some examples:
- Students are given feedback as they complete activities and revise based on their feedback.
- Students revise cool-downs and practice problems.
- Students can revise end-of-unit assessments and cool-downs.
- Students can meet with me at any time to increase a score on previous work.
- Students revise cool-downs if incorrect, and they are encouraged to ask for help if they can’t figure out their own error.
- Students can revise graded assignments during office hours to ensure successful completion of learning goals.
- Students are given a chance to redo assignments after I work with them individually.
- Students can review and revise their Desmos activities until they are graded.
- We make our own retake versions of the assessments.
- Students can do error logs and retakes on summative assessments.
- We complete the student facing tasks together as a whole class on Zoom in ASSISTments. If a student needs to revise the answers they notify me during the session.
Other advice and words of wisdom
I also asked survey participants for any other strategies that both have and haven’t worked in their classrooms. Here are some responses.
What have you tried that has not worked?
- Going over practice problems with the whole class every day. The ones who need it most often don’t benefit from the whole-class instruction, and the ones who don’t need it distract those who do.
- Grading work on the tasks within the lessons for accuracy
- Leaving assignments open for the length of the semester so that students can always see unfinished work
- Going through problems on the board with the whole class does not correct student errors
- Most students don’t check feedback comments unless you look at them together
- Grading images of student work on the classroom activity tasks uploaded by students in our learning management systems
- Providing individual feedback on google classroom assignments was time consuming and inefficient
- Allowing students to submit late and missing work with no penalty
- Trying to grade everything
- Below grade 9, homework really does not work.
- Going over every practice problem communicates that students do not really think about the practice problems on their own.
What else have you tried that has worked well?
- My students do best when I consistently assign practice problems. I have tried giving them an assignment once a week but most students lose track. It is better to give 2–3 problems or reflective prompts after every class, which also helps me get ahead of misconceptions.
- I don’t grade homework since I am unsure who completes it with or for the students.
- A minimum score of 50% on assignments, which allows students the opportunity to recover, in terms of their grade in the class
- Time constraints imposed during remote learning impact the amount and type of homework I give as well as what I grade
- Give fewer problems than normal on second chance assignments
- I have used platforms such as Kahoot to engage students in IM material. I also build Google Forms to administer the Check Your Readiness pre-assessment and End-of-Unit assessments, but I may start using ASSISTments for this in the future.
- The value of homework in high school is okay, but personally I skip good for great.
- Students are able to go back and revise their independent practice work upon recognizing their mistakes and learning further about how to solve the problems.
- Sometimes I select only one or two slides to grade instead of the whole set when I use Desmos activities.
- Allow for flexibility in timing. Give students opportunities for revision.
- Frequent short assessments are better than longer tests, and they allow students to focus on specific skills and get feedback more frequently.
- Especially during the pandemic, many of my students are overwhelmed and underachieving. I am focusing on the core content.
- Homework assignments consist of completing Desmos activities students began in class. Additional slides contain IM practice problems.
- I am only grading the summative assessment for accuracy and all else for completion. I want the students to know that they have the room to learn, try new strategies and be wrong while working on formative assessments.
Next Steps
What grading and homework policies have worked for you and your students that aren’t listed? Share your ideas in the comments so that we can all learn from your experience.
What would you like to learn more about? Let us know in the comments, and it will help us design future efforts like this one so that we can all learn more in a future blog post.
We are grateful to the teachers and facilitators who took the time to share their learning with us.
