“We are striving to . . . compose a country committed to all cultures, colors, characters, and conditions of man. And so we lift our gazes not to what stands between us, but what stands before us.”
Poet Laureate, Amanda Gorman
Amanda Gorman recited her poem, “The Hill We Climb,” on Inauguration Day. Her words were not only inspiring, but a piercing call to action. I thought about my work at IM and wondered what a commitment to “all cultures, colors, characters, and conditions of man” meant in my role. As a lead writer for the IM K–5 Math curriculum, I was dedicated to figuring out how we could infuse culturally relevant and responsive pedagogy. Our elementary writing team was committed to providing all students with opportunities to see themselves in the curriculum. As I reflect on what we accomplished, I stand tall knowing we were ready to answer Ms. Gorman’s call.
The IM K–5 Math curriculum includes support for teachers to implement culturally relevant and responsive pedagogy. Crafting the supports was among the most challenging team efforts of my career. We tried many things and failed at some. Our team included educators from a variety of backgrounds, some having had very little or no interaction with students of color. We needed time for learning and self-reflection.
Through a series of book studies, shared readings, courageous weekly conversations, and norming on “saying the thing,” we dug below the surface to understand inequities, injustices, and racism in education. It was hard work. These conversations exposed personal pain as some of us relived our own school-based racial traumas. These discussions also offered space for each of us to acknowledge our part in furthering some of these injustices as educators.
Our journey was well worth it. Through this work, we developed a common understanding of and commitment to our purpose: to use the curriculum to address the needs of marginalized students, and, in particular, Black and Brown children.
What is culturally relevant and responsive pedagogy and why do we need it?
As with many educational initiatives, culturally relevant and responsive pedagogy has shown up in many different forms, and there are several definitions. In researching the works of pioneers such as Gloria Ladson-Billings, Geneva Gay, Sharroky Hollie, and Zaretta Hammond, one clear commonality is the call on educators to build their cultural knowledge of their students, and to use that knowledge to provide instruction that allows all students to effectively learn and process information.
Build Cultural Knowledge
Understanding that there are cultural differences in the way learners make meaning is the first step. Because our goal at IM is to create “a world where all learners know, use, and enjoy mathematics,” we have employed the problem-based approach in our K–12 curricular materials.
Our dominant cultural ways of “doing school” position students as receivers of information. This traditional method of meaning-making, characterized by direct instruction and assessing how well students did what was demonstrated by the teacher, does not work for a huge swath of learners. It is an individualistic approach to learning, which excludes many learners, especially Black and Brown learners who often come from cultures that value collectivism (Hammond, 2015).
The problem-based approach supports learning for all students, whether or not they come from an individualistic or collectivist culture. The collectivist approach to “doing school” positions students as contributors to learning. Teachers engage students’ curiosity through questioning, and students use their developing knowledge and that of their peers to engage in collaborative discourse, process new information, and problem-solve. Student knowledge can be assessed by a number of indicators, including student-to-student discourse and their independent use of representations that demonstrate conceptual understanding.
In the problem-based lesson structure used throughout IM K–12 Math, students learn math by doing math. This structure centers inquiry, collaboration, and discourse as ways of meaning-making, all of which fit naturally into the collectivist approach. In a previous blog post, I shared how this structure is aligned to Zaretta Hammond’s proposed culturally responsive lesson structure: Ignite, Chunk, Chew, and Review (Hammond, 2015). Throughout an IM lesson in any grade level, students have opportunities to both independently and collaboratively process information and apply their learning. Highlighted below are features of IM’s K–12 curriculum materials that support problem-based instruction.
Mathematical Community
Students come to us with a variety of mathematical identities. To support the development of positive and productive dispositions about math, the curriculum has embedded resources to build a mathematical community that can help shape students’ positive mathematical identity. In the K-5 materials, the first unit of each course provides tools to establish norms that will position all students as capable contributors to the learning community. Beyond the first unit, there are suggestions for fostering mathematical discourse and revisiting community norms.
Instructional Routines
Instructional routines ignite students’ mathematical ideas and build on current knowledge. They provide a structured sequence of interactions for students to be curious, do math together, and share their developing thinking. Positioned at the beginning of the lesson, these routines invite students to bring their understanding of mathematics and the world to the task. Teachers can use this time to honor students’ voices and understand student thinking.
Mathematical Language Routines
Language supports deep conceptual learning. The Mathematical Language Routines (MLRs) are instructional routines that support language development and mathematics learning. These routines are positioned in the K–12 curriculum within activities, or as added supports for English learners. They provide students with structures and opportunities to make sense of language and content through constructive mathematical discourse.
Provide Opportunities for Effective Meaning-making
The lived experiences of marginalized students are often invisible in the traditional math classroom. In the research article “But That’s Just Good Teaching! The Case for Culturally Relevant Pedagogy,” (1995), Gloria Ladson-Billings says “culturally relevant teachers utilize students’ culture as a vehicle for learning.” (p. 161) Educators must work to understand the experiences of all of our students, and help them use their experiences to make sense of mathematical concepts.
Culturally responsive educators use cultural knowledge to adjust instruction and provide all students with opportunities to effectively learn and process information. To support this effort, the IM K–5 Math curriculum has a few important features to note.
Contexts from Ethnically Diverse Cultures
As writers, it was challenging to determine the context for each task. It was very important to make sure that the contexts were age appropriate and relevant to students. We also wanted to ensure that all students could see themselves in the curriculum. Understanding the influence of context on meaning-making, we knew that activities depicting the cultures of non-white, ethnically diverse people, as Geneva Gay argues in her book, Culturally Responsive Teaching (2018), “will be useful in counteracting the negative emotional and academic effects of the racism . . . embedded in both formal and informal curriculum content.” (p. 193)
In addition to providing positive representations of ethnically diverse cultures, each of these tasks needed to offer an authentic application of mathematical concepts. In other words, these problems had to make sense. Our writing process proved to be an amazing lesson about the different ways to explore mathematics in the world around us. As students engage in these tasks, they may learn about a new culture or see their own represented. They have opportunities to draw upon their own knowledge to solve problems arising in everyday life and society. (See an example of a task of this kind in a previous blog post.)
Launch into Contexts
Contexts can be either a mirror or a window, depending on whether they reflect a students’ own cultural experiences or not. As Emily Style explains, “A mirror is a story that reflects your own culture and helps you build your identity. A window is a resource that offers you a view into someone else’s experience.” (Style, 1988) When most contexts come from the dominant culture, students from that culture predominantly encounter mirrors in the curriculum, and students from other cultures predominantly experience windows. Because we included contexts from diverse cultures, all students have an opportunity to experience both windows and mirrors, and thus all students have a chance to build their mathematical identity—not just those from the dominant culture.
Sometimes, however, unfamiliar contexts can get in the way of mathematical understanding. The teacher-facing materials include supports for launching into activities within lessons. These launches include suggested questions and resources that teachers can use to provide opportunities for all students to make connections between the mathematical concepts and contexts in a given activity and their daily lives.
Grade 1, Unit 2, Lesson 19:
Launch to activity:
- “We have been solving problems about different games people play. Today we will solve problems about a game called Lotería. Has anyone played Lotería?”
- Share responses.
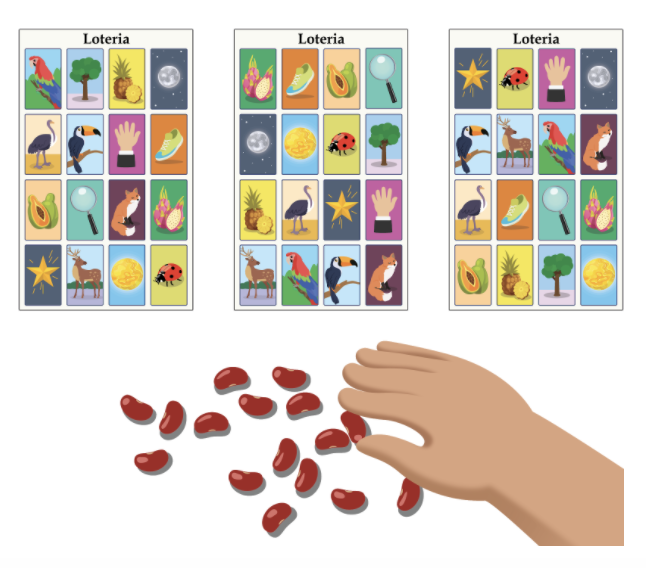 If needed, “Lotería is a very popular game played in Mexico. It is similar to the game bingo. Instead of numbers, the caller picks a card with a picture on it. If the picture is on your board, you cover it. Many people use beans or small rocks to cover the pictures. When you have four pictures covered in a row you call out, ‘Lotería!’”
If needed, “Lotería is a very popular game played in Mexico. It is similar to the game bingo. Instead of numbers, the caller picks a card with a picture on it. If the picture is on your board, you cover it. Many people use beans or small rocks to cover the pictures. When you have four pictures covered in a row you call out, ‘Lotería!’”- Consider displaying images of the game boards and picture cards used in the game.
Grade 4, Unit 5, Lesson 12:
Launch to activity:
- Groups of 2
- “On a weekday, how do you spend the hours between the time you wake up and the time you go to bed? How much time do you spend getting ready for school, going to school, and at school? How do you spend your time after school?”
- “Take a quick minute to list your usual weekday routine, knowing that it may vary from day to day. You may choose to focus only on one day—say, Monday.”
- 1–2 minutes: quiet think time
- 1–2 minutes: partner discussion
- “How did you show the amount of time you spend on each activity?” (In hours, in minutes, as intervals of time—for example, 8:30 to 3:30)
- “Let’s look at how Mai spends her day in hours and minutes.”

Context Consistency in a Series of Problems
Contexts can play different roles in mathematics learning depending on the learning goal. Sometimes, familiar contexts are used to support students in making sense of the mathematics. Sometimes, unfamiliar contexts can provide opportunities for students to apply their mathematical learning to the world to understand it better. In order for students to use mathematics to understand the world, the mathematics needs to be solidly understood. But if students are still developing their conceptual knowledge and procedural fluency in a particular area of mathematics, a series of unfamiliar and unrelated contexts within the same task can pose an unnecessary barrier to students’ learning. An unintended result is that students may ignore the contexts completely, and apply procedure-based strategies that include pulling out key words and numbers to find the answer. Strategies such as these can have the undesired effect of taking the meaning-making out of problem-solving, as the focus shifts to finding an answer rather than solving a problem. (More on problem solving in this blog post.)
In the IM K–5 Math curriculum, we frequently use the same context when there is a series of problems in an activity. When we do this, we structure the activity so that the launch supports students’ understanding of the context for the entire series of problems, thus removing a significant barrier to learning for students who are unfamiliar with the context at the outset. This ensures that students can more effectively engage in meaning-making and apply their mathematical knowledge to the task.
Here is an example of how the writing team started off writing a series of problems with unrelated contexts, and later revised them for context consistency:
Grade 5, Unit 3, Lesson 11
| Alpha Lesson (before) | Version I Lesson (after) |
Launch/Activity: Solve each problem, draw a diagram and explain your reasoning.
|
Launch to Activity:
Activity 1: Jada and her 2 sisters equally share $\frac{1}{2}$ a pan of macaroni and cheese.
Activity 2:
|
(More on how the grade 5 curriculum intentionally supports equitable teaching practices in this blog post.)
Build Relational Trust
A key feature of culturally responsive pedagogy is building relational trust. One factor contributing to the lack of trust between teachers and students is the fact that underserved students are often placed with teachers who are underqualified. In his book, Culturally and Linguistically Responsive Teaching and Learning (2012), Sharroky Hollie explains, “Over time, underserved students lose confidence in the ability of teachers to teach.” (Hollie, p. 63) He suggests teachers work to earn students’ respect by conveying content knowledge, in addition to building a rapport with students. At IM we aim to address this issue by weaving into the teacher-facing materials support for teachers’ learning of both content and pedagogy.
Another prohibitive factor to building relational trust is that teachers tend to have low expectations of students. According to the TNTP report The Opportunity Myth (2018), only 44% of teachers believe that their students can have success on grade-level standards. As a result, only 26% of lessons in their study were grade-appropriate, and access was far more limited for Black and Brown students when controlling for race. Work must be done to build mutual trust between teachers and students.
Culturally responsive educators see all of their students as capable learners. They have strong content knowledge, and provide opportunities for students to engage in grade-level content with a balance of rigor. They work with their students to set high expectations for student performance, and create avenues for students to advocate for their learning through cycles of feedback and revision. Each of these practices helps build relational trust. Below are a few features from the IM K–5 Math curriculum that support teachers in this effort.
Monitor Student Work
As a teacher I sometimes found the answer key in the teacher’s guide of a curriculum less than helpful. It would offer an answer, but it didn’t always prepare me to manage the variety of responses that would come up as students were developing their thinking. As a result, I may have dismissed student work as wrong when in fact the student was on an appropriate pathway to demonstrating conceptual understanding. In this case, the educator’s limited understanding of the mathematical progressions of learning can be a deterrent to the development of relational trust. The teacher may fail to see that student as a capable learner, and the student’s math identity may be at risk when they are unable to make connections between what they know and what they are learning.
To take some of the guesswork out of what student responses teachers may observe during the lesson, the K–5 curriculum’s teacher-facing materials include suggestions for monitoring student work. Here are two examples from the curriculum:
Grade K, Unit 4, Lesson 11:
Narrative: The purpose of this activity is for students to draw a picture to represent and solve a story problem.
Monitor: Many students may draw pictures with details—for example, a drawing of students playing soccer. Students should have access to connecting cubes and two-color counters to help them represent the story.
Grade 3, Unit 6, Lesson 10:
Narrative: In this activity, students solve problems involving elapsed time in a way that makes sense to them. Although the problem type may be new, students can reason about them using their understanding of time and of addition and subtraction. They can also support their reasoning by drawing on a clock.
Monitor: In each problem, students are given a start time and an elapsed time of 24 minutes. To find each end time, students may:
- Use words to describe their thinking.
- Write a series of numbers and symbols to show how 24 minutes is added to the start time.
- Create a table to track changes in time from the start time to 24 minutes later.
- Show incremental “jumps” that add up to 24 minutes on the clock.
- Use a linear representation to show incremental changes from the start time to 24 minutes later.
Advancing Student Thinking
While checking on student progress, teachers gain incredible insight into student thinking. They may find students at various stages of learning. The K–5 materials provide teachers with suggested questions to ask students as they are developing their thinking. These questions are intended to advance students beyond where they currently are, without telling the student where they went wrong or how to do the problem correctly. Relational trust can be built as teachers show investment in student success, and as students experience opportunities to make revisions before the activity or lesson concludes.
Here are two examples of Advancing Student Thinking from the curriculum:
Grade 2, Unit 3, Lesson 15:
|
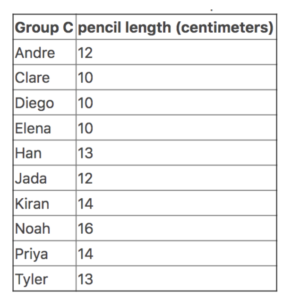
Problem: Use this data to create a line plot.
Advancing Student Thinking: If students label their line plot using only the measurements in the table (for example, they only label 10, 12, 13, 14, 16 without labeling the numbers in between), ask students to look at the line plots from the launch. Consider asking:
|
 |
Grade 5, Unit 2, Lesson 3:
Problem: Three dancers share 2 liters of water. How much water does each dancer get? Write a division equation to represent the situation.
Advancing Student Thinking: If students write the numbers in the division equation in the wrong order, ask “Can you describe how your equation represents the situation?”
Teacher Reflection Questions
At the end of each lesson, teachers have an opportunity to reflect on their lesson with teacher reflection questions. (More on teacher reflection questions in this blog post.) To support teachers with monitoring their biases, a subset of these questions focus on beliefs and positioning. Here are a couple of examples from the curriculum:
Grade 1, Unit 4, Lesson 5
What do your students think it means to be good at math? How are you helping them change negative impressions they might have about their ability to reason mathematically?
Grade 4, Unit 2, Lesson 2
Who participated in math class today? What assumptions are you making about those who did not participate? How can you leverage each of your students’ ideas to support them in being seen and heard in tomorrow’s math class?
Call to Action or Next Steps
How do you see the IM curriculum supporting culturally responsive pedagogy at your school? In what ways will you respond to Amanda Gorman’s call to action?



