By William McCallum
Our vision at Illustrative Mathematics is a world where all learners know, use, and enjoy mathematics. In my last post I picked up that first verb and talked about what it means to know mathematics. In this post I’d like to talk about what it means to use mathematics.
Now, there are any number of accounts of the uses of mathematics in science, technology, engineering, statistics, economics, and everyday life, and I won’t rehash them all here. Anybody who cooks or does landscaping uses arithmetic, ratios, rates, and units on a daily basis. And I love this video from This Old House where Tommy uses geometry to find a mitre angle. It is also true that pretty much all these uses of mathematics can be aided with technology. Cooks have calculators, or apps that recalculate all the quantities in their recipes; engineers have sophisticated software programs that solve differential equations; Tommy has a specialized tool that gives the mitre angle (although that is subject to measurement error in a way that the geometric method is not). These days, if you want to know the solution to a quadratic equation, you can just say “solve $x$ squared plus five $x$ minus 6 equals zero” into your smartphone—try it, it’s fun! Are the engineer and the cook still using mathematics if they make use of technological aids that “do the math” for them? I want to come back to this point later, but first let’s enter the K–12 classroom and visit with the learners that are the subject of our vision statement.
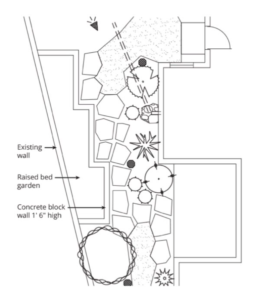
Every school mathematics teacher has probably at some point encountered the question “When will I ever use this?” My colleague Jason Zimba recently wrote a paper for a foundation interested in thinking about building an Algebra I curriculum around project-based learning, and his answer there was “How about today?” He goes on to make the case for incorporating mathematical modeling into the curriculum as a way of giving students an immediate answer to the question. In IM 9–12 Math we have incorporated modeling prompts, simple open-ended questions that call on students to use the full modeling cycle. There is even one about landscaping that asks students to estimate the cost of building the raised bed garden in this plan.
When students ask “When will I ever use this?” I suspect that the “this” in the question is often the “doing the math” part of what they are learning: executing procedures. And it’s a good question if that’s all there is to using mathematics. There is value in learning to execute procedures as a way of getting an understanding of how they work and what they can do, even if later in life you are going to use technology to execute them. However, that’s a subtle answer to the question, and the student would be justified in some dissatisfaction with it.
But there is more to using mathematics than executing procedures. An important aspect of modeling is constructing a model—expressing in mathematics the essential features of the situation being modeled—and interpreting the results of the mathematical manipulations you perform once you have done that. If you have read my previous post on what it means to know mathematics, you will remember that expressing and interpreting are key to what I think it means. If we think of using mathematics as not just “doing the math,” but using the concepts of mathematics—ratio, rate, slope, expression, equation, function, angle—then we have a good answer to the student’s question. Whatever methods are used, for example, to graph a linear function, knowing how to interpret its slope and initial value in terms of a context is important in applying it to a real-world context.
Going back to the engineer and the cook at the beginning of this post, the answer to the question of whether they are using mathematics is a resounding yes. The engineer needs to know how to interpret the solution to the differential equation; the cook needs to understand scaling.
Of course, the student who is asking “When will I ever use this?” could really be asking “When will I ever want to use this?” Stay tuned for next month’s blog post on what it means to enjoy mathematics.
