By Jen Hawkins and Mike Nakamaye
What do we do with curious students who are ready, willing, and able to go further with math ideas?
Some students cannot wait to dig deeper into the mathematics they are studying in class. Their curiosity comes from working with a dynamic and exciting math curriculum that builds their confidence. These extra-curious students, who are ready and willing to take on a challenge, will flourish when offered the opportunity to use mathematical ideas in unexpected ways. In the Illustrative Mathematics K–5 Math curriculum, these students are ready for Explorations.
What are Explorations?
Explorations are problem-solving questions and exercises that stretch students’ thinking about the content on which they are working. Explorations are found with the practice problem sets in every section of the IM K–5 Units.
We were the writers for the K–5 Explorations. As IM’s Mathematician in Residence, Mike was the primary writer, and IM Facilitator and Coordinator for the IM K–5 Math Beta Pilot, Jen, served as the secondary writer. We envision Explorations as mostly being one of two types. The first type is primarily an extension of the math in an activity: a fun way to use or explore the math that is accessible to everyone, in a slightly looser or more creative way than in the lesson. The second type goes deeper, giving students a chance to think creatively about the ideas of the curriculum and see how they apply in different situations. Sometimes an Exploration can be both types! The Explorations serve as a way to help students mentally take a stretch, or let their mind go on an unexpected detour with the content.
Kindergarten example
The Explorations are aligned with content in each section of the materials. This first example is from Kindergarten, Unit 3, Section A which is about exploring 2-dimensional shapes. Kindergartners are frequently asked to count shapes like circles, trapezoids, triangles, and rectangles within a structured arrangement. The Exploration below challenges the student to think outside of the box, or rather, in this case, inside the box. How many squares are there? What can you say about their sizes?
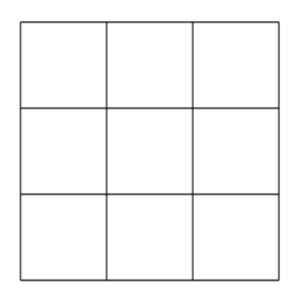
How many different size squares do you see?
How many squares do you see altogether?
The curious student working on the problem above may choose various tools to help them think: getting some 1-inch tiles to assemble and manipulate, or perhaps using color with highlighters or markers might help them as they consider the questions in the Exploration.
Grade 3 example
This Exploration problem is from Grade 3, Unit 2, Section A, where students first learn the meaning of area. A student will likely want to grab some pattern blocks to manipulate as they consider how to answer the question and explain their thinking.

Which shape has greater area, a green triangle pattern block or a tan rhombus pattern block?
Explain your reasoning.
How were Explorations developed for the IM K–5 curriculum?
We use a variety of techniques to write Explorations. We think of ways to apply the ideas of a section to a compelling situation. We look to bring in visual representations and art whenever possible. This could mean counting colorful shapes in a mosaic for kindergarteners, or using the angles in a sculpture for a grade 4 Exploration problem. In units focusing on arithmetic, we try to help students see mathematical structure that invites them to solve problems in creative and flexible ways. Regardless of the source of inspiration for the Exploration, we try to write questions that are more open-ended or underdetermined.
Grade 4 example
This Picasso painting was perfect for Grade 4, Unit 7, Section A, where students are first introduced to angles. Students discover a famous artist and work of art while looking for angles. Some students may take this further and search for angles in or outside the classroom

Name or describe any shapes that you recognize in the painting.
Do you see any parallel lines? If so, trace or circle them.
(If you’d like, you can use a different colored pencil for each set of parallel lines.)
Are there any angles in the painting? If so, mark them or describe where they are.
Another consideration for how to make an Exploration is to try to think of things “backwards” or “inside out”. By “backwards,” we mean giving the student an “end” and asking them to think backward: if this was the final result, what happened before to make this possible?
By thinking “inside out,” we mean looking at an activity or center game from inside it, from a new angle, changing something about a familiar activity from the unit or the directions in a center game.
Grade 3 example
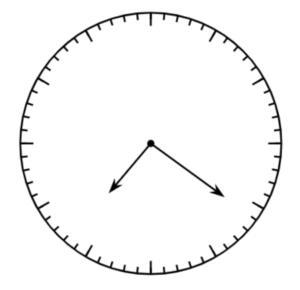
This Exploration from Grade 3, Unit 6, Section D is literally both backwards and inside out. Students are given a mirror image of a pair of clock hands and asked to determine the time shown on the clock. If students do not understand how a mirror changes an image like a clock, then this is an opportunity to get a mirror and explore! Once they understand what the mirror does, and the final result that is produced, they then think backwards to figure out what the real clock face looked like.
Jada sees this image of a clock in a mirror. What time is it? Explain your reasoning.
What research supports the importance of Explorations?
We kept in mind Norm Webb’s work about Depth of Knowledge (DOK) when writing the IM Exploration problems. The DOK framework is frequently used to evaluate the thinking demand of assessment items. It describes four levels of knowledge required to solve problems. These are, from lowest to highest:
- Recall and Reproduction
- Basic Application of Skills and Concepts
- Strategic Thinking
- Extended Thinking
In practice problems, students are typically expected to recall concepts or procedures with which they have been working in lesson activities. They may also be asked to “step it up a bit” and apply skills they have been using in familiar situations to something a bit different, but still basic. These fall within the first two levels of the DOK framework. When engaging in strategic thinking, students may apply skills in completely unfamiliar situations, or explain why a strategy works. Other problems may require a student to stretch their thinking, make new connections or examine relationships in a new way. Explorations are designed to activate this kind of strategic and extended thinking.
Why explore rather than go on to the next topic or even the next grade’s work?
So often teachers have felt the only option for a curious student was to go past the topic at hand, to move on to the next chapter, or to push a student to move faster to get to the next grade’s math. Our thinking at IM couldn’t be more different from that.
Bill McCallum, CEO of IM and co-author of the Common Core, explains why an Exploration is preferred to a jump ahead: “The basic principle here is to go deeper rather than faster. For students who have mastered grade-level content, there is still a rich world of interesting problems to apply that content to; problems that go beyond the level expected by the standards in terms of depth of conceptual understanding, facility with procedural skills, or complexity of applications. These problems give students experiences that form a foundation for a really mature understanding later in life, rather than a feeling of having done the quick 14-day tour of a foreign country that leaves little impression.”
We felt similarly. We wanted the Explorations we wrote to provide students with opportunities to consider mathematical ideas at a deeper level. This is important because a richer examination of math ideas leads to a deeper conceptual understanding. When we just move on to another lesson or into the content from another grade we are depriving students of the opportunities to strengthen the foundations of their mathematical ideas. This way of presenting the curriculum honors the depth and difficulty of the mathematics at every grade level. It is more important for a second grader to spend time understanding why strategies for adding numbers within 1,000 work—and which ones are best in different situations—than it is to start adding 4 and 5 digit numbers. For example, if a student can see that 582 + 319 = 901 mentally, because 82 + 18 = 100 then they are breaking numbers up and moving them around based on place value, important skills that will be used going forward in future grades. The flexibility gained by working deeply with content provides a strong base for future mathematical ideas to be built upon.
Which students are suited for Explorations?
“The Explorations are for any students who show an interest in them!” says IM CEO Bill McCallum. “Feeding students’ natural curiosity will give them a view of mathematics that is very different from a ‘just do the math’ approach. Indeed the very word ‘Exploration’ captures the feeling about mathematics that we want students to have: something to be explored, rich in discoveries.”
When and how should a teacher use IM’s Explorations?
Explorations can be used in many different ways.
For example, students might choose to work on an Exploration:
- during weekly “choice” time
- when a student is finished before classmates and has an interest in doing more
Teachers might use an Exploration to:
- inspire a mini-lesson for a small group
- share with parents during an Open House/Parent Night or regular communication
- support parents in starting math conversations at home
Just as important as considering when to use Explorations, we feel it is important to consider when not to use them. The intent of IM is for students to enjoy mathematics. For this reason we would not suggest Explorations be “assigned” as homework, be handed out indiscriminately as “busy” work when a teacher is engaged with a small group, or be expected to even be of interest to every student in a class.
How can Explorations serve as professional learning for teachers?
When teaching any math content, IM encourages teachers to “try the math” before they work with students. It is important for teachers to see how they themselves would do a problem, and then to consider how some of their students might solve the problem before beginning instruction and facilitation of the content. There’s no better way to open your mind than to play with mathematical ideas. Not only will you feel great about the mental exercise, but the energy it gives you will be evident to your students when you share Explorations with them, and it may very well inspire you to write your own!
Reflection questions to ask oneself when exploring Explorations:
- What does my approach to solving this tell me about my mathematical thinking?
- What will this problem bring to mind for my students? Will they need my support to explore this problem?
- How can this existing Exploration be added to in order to provide further math adventure for my students?
Questions to consider when thinking of writing Exploration problems:
- What would be interesting to explore just beyond the activity we did today?
- Can I take a detour and go someplace new with the math in this unit?
- What would a backwards version of this problem be? What math would be involved?
What else can be offered as challenging options for students with IM?
Looking for more? Here are some other ideas to keep extra-curious students engaged:
- Ask students to create a new set of rules for a center game and to provide an explanation, which can be verbal or written, of why their new rules make sense mathematically.
- Ask students to figure out the best strategy to win a center game. They could describe the strategy and provide examples of why it will succeed.
- Students can be encouraged to write an Exploration on their own. When completed, a partner who has also created an Exploration can swap and they can each try out a new exploration!
In addition to these ideas and the Explorations found in the K–5 curriculum, IM has published content tasks aligned to the Common Core. These tasks can be found here.
We hope that teachers find these ideas and the Explorations included in the practice problems in the IM K-5 Elementary program to be engaging and exciting challenges for their students. We encourage educators to explore their own mathematical ideas as they work with students: be adventurous, take math risks, try a new direction, enjoy exploring!
Next Steps
What do you currently do to support curious students who are ready, willing, and able to go further with math ideas?
What decisions made by the IM Explorations writing team will you explore in your pedagogy?
