In my role at IM, working with teachers and administrators, I am asked to help with the challenges of implementing an IM curriculum. We are often asked, “How can I differentiate instruction while using this curriculum?” or “What resources does IM offer to support differentiation?”
When we created the teaching guide for the curriculum, we chose not to use the word differentiation. This was deliberate, as differentiation is interpreted in many ways. One common interpretation is providing different instructional tasks for different students, either through differentiated student materials or by pulling small groups based on some diagnosis and providing different instruction to those groups.
We focus on access and challenge. IM K–12 Math is designed to give all students access to grade-level mathematics, by providing tasks that students can make sense of, reason about, collaborate to solve, and learn from without specifying the strategies students must use to solve the problem. The curriculum is also designed to give all students opportunities to go deeper with the content, and to make many connections between concepts. In fact, the curriculum is designed for and works best when students come up with a range of approaches (concrete, abstract, correct, incorrect, algorithmic, visual, etc.) and are given multiple opportunities to compare their thinking to peers and to the examples provided in the curriculum. All students benefit from hearing a range of ideas and connecting their ideas to the ideas of peers with different approaches.
We recognize that students come to us with a wide variety of interests, strengths, experiences with math and language, cognitive resources, etc. Providing access to grade-level mathematics does require that teachers make strategic adjustments in order for students to engage, make sense of the questions being asked, persist, collaborate with peers, share their thinking, listen to and understand each others’ thinking, internalize and try on new ideas, and practice and apply what they are learning.
Educator and researcher Rhonda Bondie suggests that teachers plan for and use differentiated instruction before, during, and after a lesson as they
- adjust common instruction: adjust the launch, directions, sequence of activities
- use specific resources: offer a support such as sentence frames to students who need access for participating in conversation with their classmates
- individualize practice: offer various practice assignments for students to choose from (2019)
What does this look like in a problem-based classroom? When we apply Bondie’s suggestions, we consider what supports are already included in the curriculum, as well as how teachers can plan to support access and challenge for all students. Let’s consider an example drawn from experiences with several teachers and coaches using IM across the country. The example is from IM Algebra 1 Unit 4: Functions, and we’ll call the teacher Ms. Goodson.
Adjust common instruction: Use a familiar context
Ms. Goodson is preparing to teach Lesson 1: Describing and Graphing Situations. She knows that the purpose of Lesson 1 in each unit is to invite students to the mathematics of the unit and that students will have opportunities throughout the first several lessons to continue to work on these ideas. The lesson goals will help her decide what is most important for all students to consider. She reads the lesson narrative and the learning goals. The learning goals for the lesson are:
- Interpret descriptions and graphs of functions in context.
- Understand that a relationship between two quantities is a function if there is only one possible output for each input.
- Use words and graphs to represent relationships that are functions, including identifying the independent and dependent variables.
Ms. Goodson next looks at the cool-down and student lesson summary. This gives her a sense of what she should be monitoring for as students work—she should listen to students talking about whether one variable is a function of the other, considering whether there is only one output for a given input, and either drawing graphs from descriptions of situations or describing situations based on graphs.
With that information in mind, she takes a look at the warm-up. It’s about buying bagels from a bagel shop. There is not a bagel shop in her town, though many students have seen them for sale in prepackaged bags at the grocery store. Ms. Goodson considers whether this is a good opportunity for students having a window into another culture, but is concerned about the complex context and complex mathematics being too big of a barrier.

This problem features a non-linear pricing scheme, which reminds Ms. Goodson of heated conversations students had during this year’s homecoming festivities where couples and groups got discounts for dance tickets. She also remembers that at the homecoming fair tickets for the carnival games were sold individually, by the half-dozen, and the dozen. She decides that changing the context from bagel pricing to ticket pricing will help her students quickly access the warm-up and maintain the mathematical intent: surfacing the idea of the output for a given input being ambiguous (for example 13 bagels could be sold for \$11.25, \$13.00, \$13.25, or \$16.25 unless the store owner always sells other quantities of bagels at the best price).
Use specific resources: Blank copies of the table
Based on previous lessons that involved completing tables of values, Ms. Goodson anticipates that some of her students might have a hard time getting started on the task of filling out the best price table. Some students may want to argue for different pricing schemes, others may feel overwhelmed by having to think about all the different possible prices for each number of tickets and narrow down to the best price. She doesn’t want students to get bogged down in calculating; she wants them to see and understand the tables and graphs that represent the ambiguous situation versus the situation where price is a (non-linear) function of number of tickets purchased. Therefore she decides to print blank copies of the table of each person’s pricing scheme from the activity synthesis to have on hand as needed for groups that are struggling to get started on the best price table.
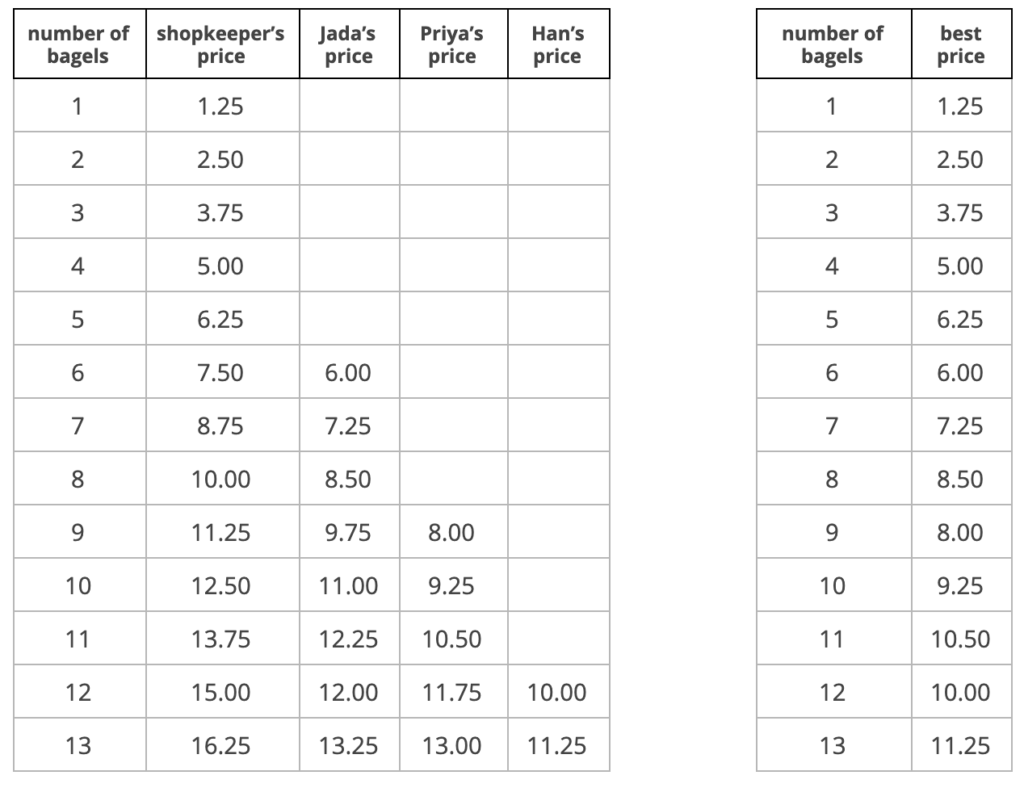
Her goal is for all students to be ready after 7 minutes of group work time to participate in a conversation about why price is not a function of number of tickets purchased, but best price is.
Use specific resources: Manipulatives
Ms. Goodson also has an idea about Activity 2: Be Right Back! While it’s unusual for dogs to be tied up outside of stores in her community, it’s pretty common for a dog to be tethered in a yard. However, some of the emerging bilingual students in her class might still have a hard time understanding the descriptions of how the dog moves around the post. How could they engage in a conversation about what the graph should look like if they’re having trouble visualizing or asking questions about the situation?
Ms. Goodson reads the suggested supports for English learners and students with disabilities, and plans to launch the task as written in the curriculum, demonstrating the dogs’ action on Day 3 using a stuffed dog leashed to a spool of thread and inviting multiple students to use the toy dog to show how they interpret the story, and then share how they might sketch a graph of the dog’s distance from the pole over time. She makes sure that she has enough toy animals and spools of thread to offer them to small groups as needed to support their sense-making and conversations. She is confident all groups will be able to get started after that launch, but that they will still have to work hard to both translate the words into actions and the actions into a sensible graph.
Individualize practice
As Ms. Goodson studies Activity 1.3: Talk About a Function, she realizes that there are multiple opportunities to individualize practice and give students different amounts of scaffolding to continue to move towards the learning goals. The task itself gives students the opportunity to make a choice about which pair of variables they choose, and she realizes that some pairs of variables might be harder than others. She also thinks about ways she could provide more access, challenge, and choice for students.
She might:
- Assign some students an activity from the aligned Algebra 1 Supports lesson which gets to the same learning goals but involves matching rather than creating your own graph.
- Assign students a particular pair of variables to focus on first, one that she knows will be accessible and will help them get started with confidence.
- Create a worksheet for students to help them remember to answer each of the questions and include sentence stems to help students explain their ideas, not just write their answers.
- Encourage students to brainstorm additional pairs of variables, and choose one pair to focus on.
- Give students the challenge of making up their own story for a partner to graph.
- Use a website such as graphingstories.com to find more examples, based on videos, which might give students more access than a written description. She notes that in the graphingstories.com handout time is already on the x-axis. Since she would like students to make a choice about which variable to put where, and how to scale the axes, she would need to provide blank graphs.
Given what she sees in Activity 1.3, and what she knows about the cool-down and lesson summary, Ms. Goodson decides that while students are doing more individualized practice during Activity 1.3, she will monitor and note students who might struggle with the cool-down, which is very similar to the practice. She knows that students will have more opportunities in the next lesson to show what they know, so she decides to invite a few students to come to her desk to work on the cool-down collaboratively. Then they spend time reading and highlighting key ideas in the student lesson summary, so she can better understand what makes sense to them now and what they are still grappling with. She will continue to monitor these students’ understanding throughout the next several lessons since the cool-down guidance states that students will have more opportunities to work on these mathematical ideas. There is no need to “press pause” until Lessons 4 or 5 if students are not yet able to evaluate and interpret equations given in function notation.
Whew! That is a lot of decisions to make, but Ms. Goodson has been watching and listening to her students and uses many of the suggestions and supports already built in the curriculum and the lesson plan. Ms. Goodson spends her planning time thinking about how she will make adjustments to support her students, rather than having to create lots of additional materials or come up with different standards-aligned activities for different students.
Next Steps
Consider an upcoming lesson.
- What supports for access and challenge are already included in the lesson?
- What can you ask, amplify, or adjust during common instruction to provide additional access or challenge?
- What specific resources can you offer students who need additional access or challenge?
- How can you individualize practice using:
- Practice Problems (including Exploration problems in K–5)?
- Are You Ready for More? (6–12)
- Student Lesson Summaries? (6–12)
- Math Modeling Prompts (9–12) or optional culminating lessons (K–12)?
