By Kate Nowak, IM Vice President of Curriculum Development and Portfolio
“The more intensely interested a teacher is in a student’s thinking, the more interested the student becomes in his or her own thinking.”
—Eleanor Duckworth
If you’re reading this you probably already know that at IM we’re big fans of problem-based learning. Stated simply, that means giving students a chance to figure something out before you show them what to do. I’m going to take it as a given that this approach is good for learning, but to read more about that, check out the National Academies’ publication How People Learn which synthesized years of research.
Through IM’s Learning Lab IMpact program, my colleagues and I have had the privilege to visit hundreds of classrooms this school year. We’ve witnessed kids and teachers, admins and coaches, in the most stressful year anyone can remember, doing amazing things. We’ve seen lots of cases of teachers seizing opportunities to use student thinking to illustrate or encapsulate a mathematical idea for the class, as well as some of these opportunities missed.
From this vantage point—which is a unique one, getting to see a day in lots of different classrooms and observing many more through video footage—I want to make two recommendations for areas to focus teacher coaching that might lead to taking advantage of opportunities to leverage student thinking.
Recommendation 1: Use teacher learning time to deepen understanding of representations that are used through multiple grades.
The specific representations depend on the concept and the grade. In a perfect world, any grade n teacher would be able to draw and describe not just the various representations used as tools for thinking and tools for problem solving for the different concepts in grade n, but also grades n – 1 and n – 2. For middle grade teachers, I’m talking about representations used in upper elementary, like base-ten diagrams, tape diagrams, number lines, arrays, and area diagrams. While there are many potential avenues for strengthening mathematical knowledge for teaching, deepening understanding of these representations across grades is particularly powerful.
Why would this be so powerful? In order to realize the potential of problem-based instruction, a teacher needs to understand and be able to recognize some different, productive ways of approaching the same problem. If you are familiar with the 5 Practices for Orchestrating Productive Discussions, we’re talking about the “anticipate” practice. The teacher materials in IM K–12 Math assist by anticipating different approaches. However, listing student approaches to look for in the teacher materials doesn’t automatically translate to every teacher knowing what those approaches are going to look like in the wild. So, it would make sense to work through strategies and understand the representations that students may draw from as part of planning a unit.
Take this grade 7 number talk warm-up:

If students experienced instruction in earlier grades leading to conceptual understanding of dividing a number by a fraction, we might see work like the following for 2 ÷ ⅓:
“How many groups of ⅓ are in 2?”

Or like this:
“How many are in each group if 2 is ⅓ of a group?”
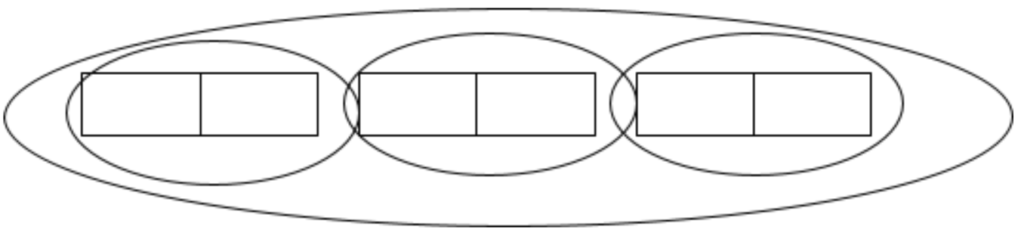
Meaning we’d see a student draw or describe a diagram like this to explain how they reason about 2 ÷ ⅓. This is sufficient for explaining why 2 ÷ ⅓ is 6. However, if the student’s grade 7 teacher hasn’t prepared to recognize tape diagrams as a tool for thinking about dividing by a fraction, that teacher might only view students using “keep change flip” as using a productive approach, and the class would miss an opportunity to use representations to strengthen their number sense and make connections to prior learning.
How to work on deepening understanding of representations used in earlier grades? We have plans for a more straightforward answer in the future, but today, I’d recommend using the unit dependency diagram or the curriculum adaptation pack to identify which unit(s) are conceptual precursors to the one you plan to teach, and start with reading its unit narrative(s) for information about representations. For a deeper dive, study the precursor unit(s) more in depth to see representations that are anticipated or explicitly taught for that concept. Another fantastic resource is the progression document for the relevant category.
Recommendation 2: Plan to display student work and a way to make it happen very quickly.
When you’ve created an environment conducive to problem-based learning, and you’ve launched the problem so that all students engage in thinking about it, different students are going to come up with different approaches, and you are going to want to talk about it. When there’s a plan for displaying student work throughout the lesson, we often see student thinking driving the conversation. If there’s not a mechanism for quickly displaying student work, we often see a teacher demonstrating the way they think about the problem.
It’s really hard to talk about something with a group if you can’t all look at it. So this tip is a logistical one, but it’s very often a prerequisite to having a meaningful discussion the entire class can follow. Everyone has to be able to see what you’re talking about.
So, plan ahead for how student thinking will be made visible to the class. We have seen this done successfully in a number of ways. Here are some examples:
- Students work in groups of 2–4 on a whiteboard that is mounted to the wall, or on a whiteboard that’s about the size of the top of a desk that can be propped up on a ledge.
- The teacher uses a tablet or smartphone to take photos of student work and has a way to quickly send them to be displayed on a projector.
- A document camera is turned on, hooked up, and can be routed through the projector at the touch of a button. A student’s paper, workbook, or the teacher’s device can be slid under the camera.
- In schools accessing IM K–12 Math through Imagine Learning (formerly LearnZillion), students can share their thinking in a digital workbook on the Imagine Learning Classroom platform, or upload a photo of their work.
Of course, cases where instruction is remote or hybrid require a solution tailored to the local context. The principle is the same: that if you want to make student thinking visible and display it to support discussion about it, it’s necessary to plan for it. IM educators have been developing ingenious solutions for their unique constraints throughout the pandemic. For some examples and inspiration, check out IM’s Distance Learning webinar from fall 2021.
Next Steps
We’d love to hear more about your workflow for making student thinking visible and displaying it to a class, and about your forays into learning about representations across grades. At IM’s Facebook or Twitter spaces be sure to use the hashtag #LearnwithIM!
