By Tashana Howse, IM Certified® Facilitator
The relationship between fractions, ratios, and proportions is introductory to students’ development of the study of Algebra. Therefore, it is important for students to engage in ratio reasoning that positions them to reason proportionally.
Consider this task:

How did you begin to solve this task? What relationships did you consider?
Here is how some students described their thinking:
Alex said: “Both mixtures are the same because each has one more lemon than water.
Emmanual said: “Mixture A has a stronger lemon taste because 3/5 of the whole mixture is lemon and 4/7 of Mixture B is lemon and 3/5 is larger than 4/7.”
Sifi said: “Mixture B has a stronger lemon taste because in Mixture A is 3 lemon equals 2 water so 1 lemon equal 2⁄3 water and Mixture B is 4 lemon equals 3 water so 1 lemon equals 3⁄4 water and 3⁄4 is more than 2⁄3.”
Beatriz said: “In Mixture A if you had 6 cups of water you would have 9 cups of lemon and in Mixture B if you have 6 cups of water you would have 8 cups of lemon and 9 is more than 8 so Mixture A is stronger.”
Who do you agree with? Why?
These relationships explore thinking in absolute terms and relative terms (Nolan, Dixon, Roy, & Andreasen, 2016). Reasoning in relative terms builds the conceptual foundation of proportional reasoning.
Absolute Terms
Alex thought in absolute terms. In absolute terms, you may notice that mixture A has 3 cups of lemon juice and mixture B has 4 cups of lemon juice. Therefore, mixture B has a stronger lemon taste.
Relative Terms
Part-to-whole relationship
In relative terms, Another way to think about it relatively is to think of the ratio of the number of cups of lemon juice compared to the number of cups of water, which is a part-to-whole relationship.

Emmanuel engaged with this kind of thinking. In the part-to-whole relationship, you may reason that lemon juice is more than half of both mixtures. More specifically, lemon juice is one half of a cup more than half of the overall mixture for both mixtures.
However, you will note that half of a fifth cup of lemon juice is larger than half of a seventh cup of lemon juice. Therefore, Mixture A has a stronger lemon taste.
Part-to-part relationship
When considering the part-to-part relationship, you may reason that the ratio of lemon juice to water is 3:2 in mixture A, while the ratio is 4:3 in Mixture B. Unpacking this reasoning further could lead into two directions: obtaining equivalent ratios or finding unit rates.
Equivalent ratios
In obtaining equivalent ratios, you would consider the following picture:
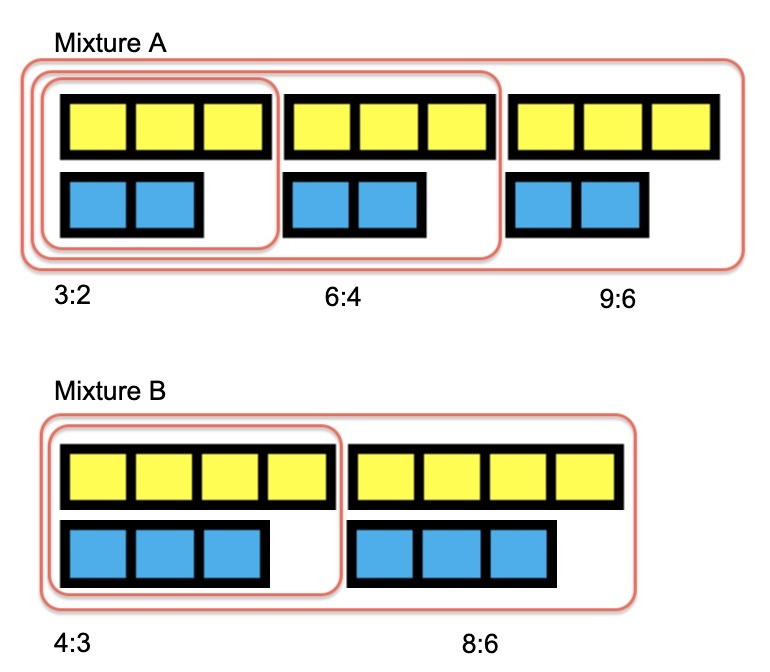
Use of equivalent ratios allows us to compare the cups of lemon juice to the cups of water. In Mixture A, 9 cups of lemon juice would be mixed with 6 cups of water. In Mixture B, eight cups of lemon juice will be mixed with 6 cups of water. Therefore, Mixture A has a stronger lemon taste than Mixture B. Beatriz engaged with this reasoning.
Unit rates
In finding unit rates, you would want to find the amount of water needed for one cup of lemon juice. In Mixture A, one cup of lemon juice calls for ⅔ cups of water. In Mixture B, one cup of lemon juice calls for ¾ cups of water. Sifi engaged with this reasoning. However, Sifi incorrectly stated that Mixture B has a stronger lemon taste. Mixture B contains more water than lemon juice, so therefore, Mixture A contains the stronger lemon taste.
Building an Understanding of Ratios
As students move from elementary to middle school, they bridge their knowledge of ratios from their experience with fractions. Fractions are special types of ratios as they are ratios that contain a part-to-whole relationship. The introduction of ratios begins the process of abstract reasoning, which is needed for transitioning to high school mathematics. Ratios contain multiple relationships, i.e. part-to-part, part-to-whole, and whole-to-part. “As students progress through middle grades mathematics, both absolute and relative thinking about ratios are important in relating quantities to one another” (Nolan, Dixon, Roy, & Andreasen, 2016, p. 49). Moving between absolute and relative ways of reasoning about ratios equip students in being able to make sense of proportional relationships. Contextual tasks like the one above allow students to experience the mathematics. The experience ignites conceptual understanding, which helps students to internalize their learnings.
Examining Student Work
Let’s return to the student work. Are the students above ready to move forward with a lesson on proportional reasoning? This can be determined by analyzing students’ reasoning. By doing so, we can determine the appropriate supports needed as students engage in proportional reasoning.

When providing feedback after analyzing student work, it is important to situate the feedback in student work. The goal of the above task was to assess students’ preparation for engaging in proportional reasoning. As stated earlier, relative reasoning builds entry into reasoning proportionally. Alex’s feedback would include a question that will prompt her to think in terms of the whole amount. For example, “How does three parts in Mixture A represent the same as four parts in Mixture B? The next question would be, “How many total parts are in Mixture A and then in Mixture B? Rather than giving the answer to Alex, questioning engages her in metacognition, which allows him to determine her own misconception for moving forward. Similarly for Sifi’s feedback, a question related to the unit of ⅔ in Mixture A and the unit for ¾ in Mixture B. By thinking in terms of the unit, Sifi will see that the ⅔ in Mixture A represents a unit of water and ¾ in Mixture B represents a unit of water. This realization will assist Sifi in noticing his misconception. And lastly, based on Emmanuel and Beatriz’s reasoning, it is evident that both students have a solid foundation in their understanding of fractions, ratios, and comparison of fractions and ratios. They both are ready to move forward on a proportional reasoning lesson.
Next Steps
Making use of student work provides teachers with instructional directions for a particular concept. Having an understanding of the learning progression of proportional reasoning enables teachers to meet students where they are.
