By William McCallum, IM CEO
co·her·ence
noun
- the quality of being logical and consistent.
- the quality of forming a unified whole.
One of the things I am proud of about IM K–12 Math™ is its coherence. This shows up in many ways: it follows a logical and pedagogically appropriate progression of ideas, it makes connections between different ideas, there is a consistency to the lesson structure and the instructional routines, and there is consistency in the use of representations. In this blog post I’d like to talk about that last aspect of coherence, which I think is often overlooked in mathematics curriculum.
One way of judging the coherence of a curriculum is to look at it as a story, and ask yourself if the story makes sense. In a real story, the characters grow and change from chapter to chapter and we learn more things about them as time goes on. But we always know they are the same person; the author establishes a consistency and believability about them, so that as we come to know them better we understand that who they were before is still there in who they are now. They may look different, but that’s because they are wearing different clothing or behaving in new ways, not because they have changed into someone else.
In the story of mathematics, the characters are the concepts, and the representations we use for those concepts are the different ways we see them as they grow. So it’s important to establish a progression of representations that are connected. We should be able to see the previous representations in each new one.
A good example of this is the way we represent numbers in elementary school. In kindergarten we start with a concrete representation, a collection of objects, which students can count as they learn their first important lesson about numbers: the connection between counting and cardinality. The initial concept of number is as a quantity of things.

Included in the objects students count could be connecting cubes.
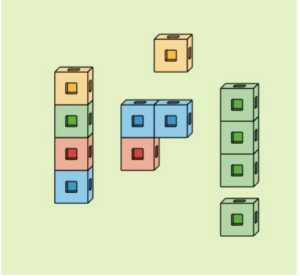
These provide an important bridge to the next representation, a bundle of ten.
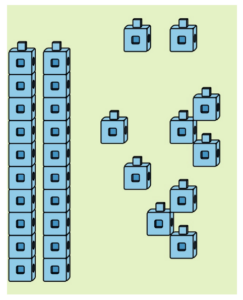
To count large collections of objects, students group them into 10s, and start to learn about the base-ten system.
As students start to learn about fractions, they see an important change in their concept of number, from being a count of discrete things to being a measurement of a continuous quantity, such as length. This is a huge shift. If the concept of number is a character in a story, you could say that the character has grown into adulthood. How do we handle the representations in such a way that students see that a fraction is still the same character, not some completely new thing? This is especially challenging because the way we add fractions doesn’t look at all like the way we add whole numbers. Students are to be forgiven for thinking it is an entirely different animal.
In IM K–5 Math™, students start to make this shift when they start using chains of connecting cubes to measure lengths.

Thus the objects they used to count now become units of measurement. At some point these chains of connecting cubes become abstracted into tape diagrams, which students start to use to solve word problems.

At this stage the concept of number is in transition. On the one hand, we are using tape diagrams to solve word problems about counting (How many more does Diego have than Mai?). On the other hand we have established the squares in the tape diagram as a unit of measurement of length. Later on the tape diagram morphs into a ruler,

and the ruler morphs into a number line.

The original counting concept of number is embedded in the number line: we get to the number 4 by counting the intervals starting at zero, the intervals that used to be squares on a tape diagram that used to be number cubes in a chain that used to be objects scattered on the table. Counting the intervals rather than counting the tick marks is important when we start to subdivide the number line into smaller units in order to create fractions. A common mistake students make when partitioning a number line into fourths, say, is to put four tick marks, ending up with fifths.
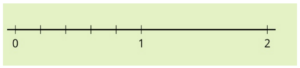
Through this progression of representations, students can see fractions not as some new beast, but as a continuation of the idea of a count, only this time we are counting smaller units of measurement. And addition of fractions becomes a matter of making sure we are measuring the two fractions using the same unit, with a common denominator.
Thinking about representations in the way I have described leads to some important principles in designing curriculum. First, we should be parsimonious in our use of representations. If we have a new representation of the same concept every day, it’s more difficult to see the concept itself. The novelty of the representation becomes the center of attention. Second, representations should function as tools for thinking about the concept, not merely as depictions of the concept. You can depict 1/4 as a segment of a circle. But if you want to explain why 1/4 = 3/12, a tape diagram is better. And third, new representations should be visibly connected to the previous ones. The progression of representations should show growth of the character, not transformation into something completely new. With these principles we can help students see the story of mathematics as a coherent whole, rather than as a jumble of disconnected episodes.
