By Margaret Betts, IM Certified® Facilitator
If story problems are your teacher kryptonite, you aren’t alone. Story problems are mathematical situations expressed with words. The element of reading creates an added layer of complexity which in turn makes it more challenging for students to understand.
IM has excellent routines in place to allow students to slow down and make sense of what is happening in the problem. IM Grade 2 Lead Author Deborah Peart wrote a wonderful IM blog post, “Making Sense of Story Problems,” about two of the key math language routines for elementary students. However, some students, particularly English learners, need specific vocabulary instruction and practice to understand some of the more nuanced language. There are some words, like “fewer,” that can take on different shades of meaning depending on the context. Trying to explain this to primary grade students has always felt like trying to hold a wet fish. This year, I partnered with an experienced classroom teacher at my school to design and teach a 30-minute lesson using the IM lesson structures and centers to engage students in the production of this word to build meaning.
Fewer: A complex idea
The word “fewer” at first glance isn’t overly challenging. First grade students can almost always identify which number is greater and which number is fewer. But like many words in English, “fewer” has multiple meanings. Within that gradation arises a pretty abstract idea.
Here is an example of the complex way fewer is used in first grade.
The ferris wheel can hold 20 people.
The swings can hold 14 people.
How many fewer people can the swings hold than the ferris wheel?
(IM First Grade Unit 8 Lesson 6 Compare Story Problems)
The context of the story is easy for my students to understand. Ferris wheels and swings are easy to illustrate with a quick video or a few images. It would also be fun to act out. Most of my students in Massachusetts have been to the country fair and have seen or ridden these rides.
The most basic meaning of fewer is a concrete comparison between two items—14 people as compared to 20 people. Fourteen is fewer than 20, so fewer people can fit on the swings than the ferris wheel. In that circumstance, there is no additional operation or work to be done. The student just needs to be able to identify the lesser amount.
The complexity comes with the slightly different meaning of “fewer” that the story problem is asking. Students are not merely comparing the numbers, they also must find the difference between those two numbers.
In the problem above, the swings can hold 6 fewer people than the ferris wheel. If asked in the inverse “How many more people does the ferris wheel hold than the swings?” Those extra seats or people could be seen and physically counted. But the question “How many fewer people does the swing hold than the ferris wheel” is asking the students to count something that isn’t there. Those people and those seats don’t exist. Students are being asked to find the absence of people.
This abstract idea happens when a number modifies the word fewer. Students have to hold the idea that there is a fewer total amount plus a fewer comparison amount. Thus students often get stuck in circular logic when trying to solve the problem.
The student/teacher exchange might go like this (trust me, I have been in this exchange many, many times):
Teacher: How many fewer people can the swings hold than the ferris wheel?
Student: Fourteen.
Teacher: Yes, 14 is how many people swings can hold. But how many fewer people can the swings hold than the ferris wheel?
Student: Fourteen?
Looking for a concrete way to show it, the teacher might ask the student to draw a picture or use blocks to show the seats for the ferris wheel and the seats for the swings..
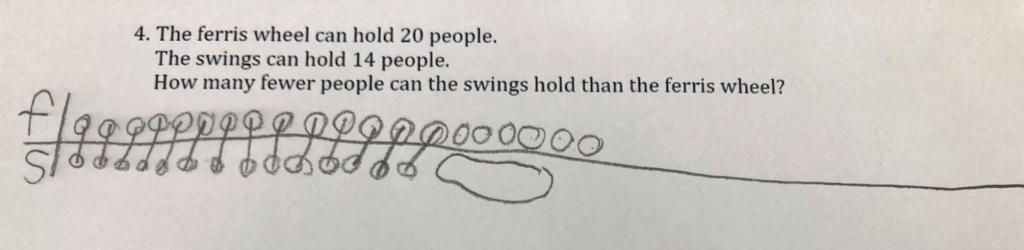
Pointing to the missing matches, the exchange could continue:
Teacher: So, how many fewer people are on the swings?”
Student: (Looks at the empty circle) “Zero?”
Now the teacher and the student are left feeling frustrated and each misunderstood. Strategies that typically work (draw a picture, model it), are insufficient in this situation, because the complexity is rooted in understanding or misunderstanding the vocabulary. In situations like this we must devote special attention to the vocabulary’s meaning in order for students to understand the mathematical idea.
Launch: Focusing attention on the essential vocabulary word
Vocabulary development is “central to learning to read, write, speak, listen to and make sense of mathematics.”* In this case, the various meanings of the word “fewer” are creating conceptual obstacles. But how do you address this problem without relying on “key word” instruction? I recently taught this lesson with first grade students at my school. Below is a description of the lesson and the work students did.
I began the launch by highlighting the dilemma to students. I told them that I had been noticing that there is a word that is very tricky to understand: fewer. I gave them an example:
There are 8 jellyfish swimming in the ocean. There are 3 sea stars in the ocean. How many fewer sea stars are there than jellyfish?
I read the problem with students using the three reads protocol, which they are familiar with. I then asked students to solve and asked for them to show their answer with fingers.
I was looking to highlight the possible answers of 5, 3, and 0. I told them I saw those three solutions and we spent some time looking at why all three seem like good ideas. After seeing that the problem was asking for us to find the difference between the number of jellyfish and the number of sea stars, I synthesized the discussion, explaining that in English when we hear the question “How many fewer sea stars than jellyfish?” the phrase “how many fewer ____ than ____” is asking us to find the difference.
Activity: Providing practice with the language
Now students need deliberate practice with the language. I found a game that lends itself to partners needing to use the word “fewer” in the particular way I wanted students to practice. IM K–5 Math has several beautiful kindergarten game boards that can be used beyond the kindergarten level. Math Libs, a center originally introduced in Unit 4, is one such option.
The Math Libs boards are vibrant and have concrete visuals. It has a place to record the total of each item. Here is an example of one board:

Then, I wrote a script to be used alongside a partner game. I easily added the script to the game board.
In the center, students roll and combine two dice to generate the number of seaweed and the number of jellyfish. The script alternates so that students get experience with asking and answering “how many fewer than” questions. To help students track the phrases, I alternated the color of each role.

While students worked, the classroom teacher and I monitored students’ language use and problem solving. Finally, I used what we heard and saw to guide students in a lesson synthesis.

Lesson synthesis: Using the 5 Practices structure
Many IM lessons are designed to support the use of the 5 Practices for Orchestrating Productive Discussion (Smith and Stein, 2011).:
- Anticipating
- Monitoring
- Selecting
- Sequencing
- Connecting
Anticipating: I had anticipated that the word fewer in this context would be challenging and I also anticipated that students would most often misunderstand it in two specific ways—renaming the total number of the fewer object (more common) or saying there is no difference (less common).
Monitoring: After launching the game, the classroom teacher and I observed students and took note of who was using the language precisely, as well as imprecisely. While monitoring, I was simultaneously looking for student thinking or work to amplify—that I would select and sequence—for the final discussion.
Selecting: I selected students who I heard self-correct as well as partners who helped explain the idea.
Sequencing: I sequenced the ideas I wanted to share, starting with the language partners used to explain and ending with one student self-correcting.
Connecting: Finally I posed a related problem to the whole class. We chorally read the script and solved the problem together. The game boards were left with the classroom teacher to continue playing and using the language in context.
Next Steps
The teacher reported that students enjoyed playing the game and it promoted their use of the vocabulary. The game is now a part of the center rotations. By adhering to the IM lesson structure (launch, activity, synthesis), using a predesigned game, and using the 5 Practices to guide my own teacher practice, I was able to teach a lesson to address a vocabulary misunderstanding.
This same model could be used to address other vocabulary struggles you are having happening in your school or classroom. I’m so curious what your tricky word or phrase might be.
References
*https://pubs.nctm.org/view/journals/mt/107/1/article-p28.xml
