By Courtney Ortega, IM Certified® Facilitator
I was recently in a meeting where a participant declared, “Grade 8 and Algebra 1 basically have all the same standards.” Have you ever wondered this yourself? Have you heard colleagues share this sentiment?
At first glance the grade 8 and Algebra 1 content standards appear to be quite similar. Grade 8 teachers often share that it can be hard to know where to stop and Algebra 1 teachers often share that it can be hard to know where to start. As we study the language of the standards, we can look for verbs and other nuances to help us make decisions. We can also study the IM 6–12 Math curriculum to explore the coherent progression of ideas and expectations from grade 8 and Algebra 1.
Seeing the structure of equivalent equations
In both grade 8 and Algebra 1, students reason about equations by looking for and using mathematical structure. This builds from understandings developed in previous years, including work in grade 6 and grade 7 on maintaining equality in equations with one variable, or reasoning about equations written in simpler forms like px + q = r.
In grade 8, students solve linear equations with variables on both sides of the equal sign. By expanding their ability to manipulate algebraic equations, students discover that equations can have no solutions, exactly one solution, or infinitely many solutions.
In Algebra 1, students continue their exploration of the structure of equations and determine conditions for when you might want to write an equation in certain forms. They need to rewrite and reason about equations in order to find solutions, and justify why each move keeps each subsequent equation true and maintains the solutions of the original equation.
In both grade 8 and Algebra 1, the work of manipulating equations will look quite similar, but our reason for doing so is slightly different. We see this in Unit 4 Lesson 7. During the activity “What’s the Equation,” students make use of structure to reason that equations which are always true for any value of the variable have equivalent expressions on each side.

In Algebra 1 Unit 2, students continue to rewrite equations using their understanding of the structure of equations. In Lesson 6 Activity 3, “What’s Acceptable,” students identify moves that create equations with the same solution. Here is a part of that task:

In the grade 8 task, students are using a knowledge of equivalency to generate equivalent expressions. They are being asked to “interpret solutions in the contexts from which the equations arose.” In Algebra 1, students are analyzing whether an algebraic move results in equations with the same solution, and why. They investigate “different ways to express the same relationship or constraint by analyzing and writing equivalent equations.” The idea of reasoning logically about expressions and writing equivalent ones is in Algebra 1 because it’s more sophisticated, and it is also no longer limited to linear expressions. Algebra 1 offers more opportunities for students to apply the concepts and skills from grade 8.
Solving Systems of Linear Equations by Substitution
Both grade 8 and Algebra 1 students study different ways to solve systems of linear equations. In grade 8, students are first reminded that the coordinates of a point that lies on a graph of a linear equation make the equation true. They then explore the significance of the point of intersection of a graph of two linear equations. In Algebra 1, students revisit their grade 8 understanding of systems of linear equations. They quickly realize the limitations of solving systems by graphing and substitution and uncover a new strategy: elimination. Because substitution is a strategy that appears in both courses, it is easy to accidentally over- or under-teach it. It is helpful to know the role that substitution plays in each course so that Algebra 1 students don’t feel that it is a redundant learning experience.
In Grade 8 Unit 4 Lesson 13 Activity 1, “True or False: Two Lines,” students use what they know about equivalence to reason that if y=2x+4 and y=-x+10 intersect at the point where y=8, then 2x+4=8 and -x+10=8. Therefore we can also say that 2x+4=-x+10. Now students have a new strategy for finding the solution to a system of equations: substitution.
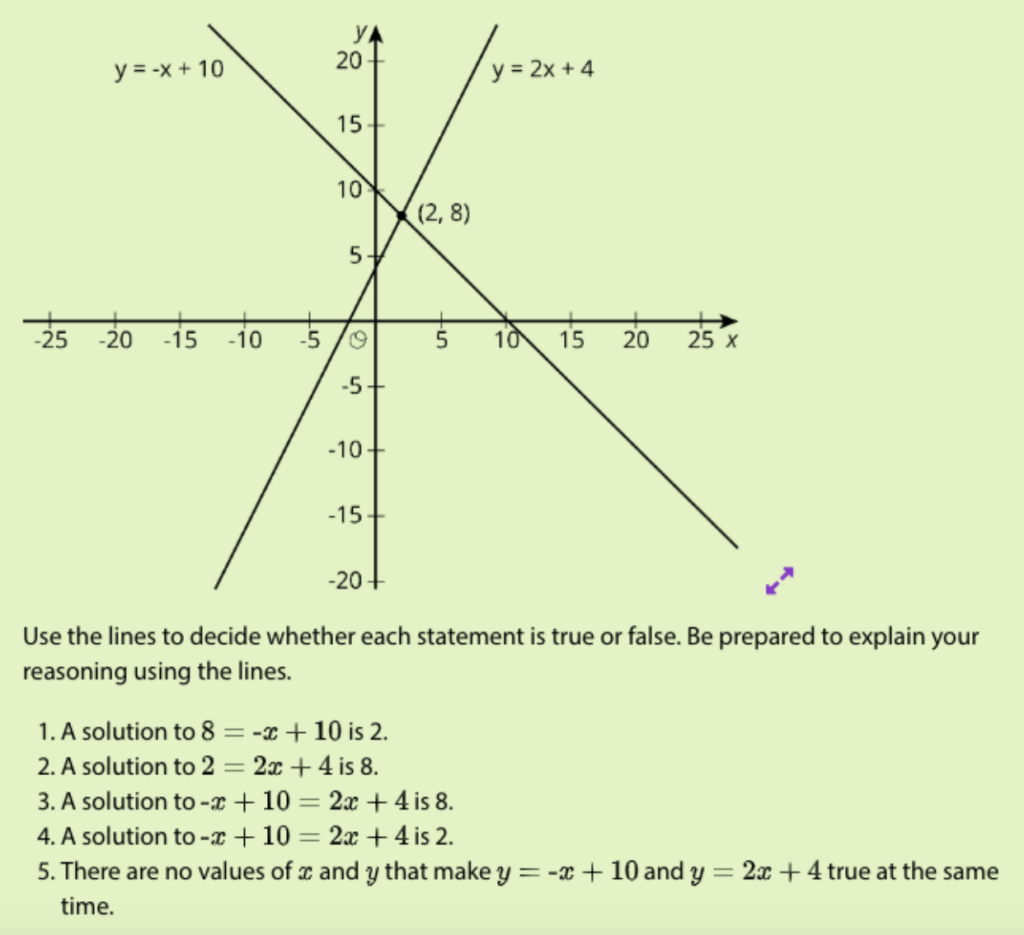
In Algebra 1 Unit 2 Lesson 13 Activity 3, “What about Now?,” students build on what they know about solving by substitution from grade 8 and explore more ways to use substitution as they encounter equations written in more varied forms.

In the system where students are solving for d and f, students might choose to use their grade 8 knowledge to substitute 18-4f for 2d in the first equation. Taking a different approach in the system where students are solving for m and p, students might choose to substitute 2m+10 for p in the first equation. Both approaches are valid and show a deep understanding of what the solution to a system means.
The concept of substitution is complex because it requires understanding of equivalent expressions, and also the strategy of using equivalent expressions to rewrite systems in ways that are amenable to solving. Because this concept pulls together so many big ideas, it is valuable for students to visit it in both courses, with an increasing level of complexity. Knowing that students will have more time to work with substitution the following year takes some pressure off of grade 8 teachers. This also means that Algebra 1 students are not starting from scratch so there is prior knowledge to build from.
Exploring Functions
Another topic that both grade 8 and Algebra 1 students study is functions. In grade 8, students are introduced to functions as a rule that assigns exactly one output to each input. They interpret graphs of functions by describing them as increasing or decreasing between specific points on the graph. In Algebra 1, students extend their understanding of functions to interpret and use function notation as well as compare key features of graphs, including domain and range.
We see the focus on the proportional relationship between two quantities play out in Grade 8 Unit 5 Lesson 8 Activity 2, “Proportional Relationships Define Linear Functions.” Students realize that the slope and vertical intercept of a linear function are the rate of change and initial value of the function.
In Algebra 1 Unit 4 Lesson 10, students focus on input and output values to learn the terms domain and range, as seen in the activity synthesis for Activity 3, “What about the Outputs?”

In both lessons, students connect what they already know about features of linear equations to new relationships such as linear functions and other functions. A strong foundation in linear functions from grade 8 is critical so that students are able to make connections between lots of different kinds of functions. Algebra 1 moves into absolute value and inverse functions, as well as exponential and quadratic fractions. Algebra 2 continues this journey with exponential, logarithmic, and trigonometric functions. In each course, students add more layers to their knowledge of functions, but always building from what they already know about functions. How does knowing how to identify key features of graphs of linear functions support their learning of other kinds of functions? Again we see that there is a clear coherence of concepts that build, rather than discrete topics that start and end within a single course.
Conclusion
Grade 8 and Algebra 1 are distinct courses; Algebra 1 is designed to build from grade 8. We see the intentional way that students continue to deepen their conceptual understanding and have multiple opportunities to revisit concepts with increasing levels of complexity.
How might a teachers’ instruction be different if the development of these concepts are understood to be a part of a longer journey, across grade levels? What if grade 8 and Algebra 1 teachers studied units and did math together? How might strengthening collaboration between teachers of these two courses support planning?
