By Courtney Ortega, IM Certified® Facilitator
Learning takes time. Students make connections, deepen their understanding, and address misunderstandings. It can make the learner feel vulnerable. “When we learn, we actively work to make sense of an idea that does not make sense to us yet,” Amanda Jansen writes in Rough Draft Math (Stenhouse, 2020). In a safe space for learning, students will share something that Jansen calls rough draft thinking, which happens when students “share their unfinished, in-progress ideas and remain open to revising those ideas.” This vision of a class that welcomes rough draft thinking is in line with the vision for an IM classroom, and there are structures already embedded in IM K–12 Math™ to support this work. Let’s explore some of the ways that the IM curricula encourage revision.
Revision is a Critical Component of Problem-Based Teaching and Learning
The figure below illustrates the elements of problem-based teaching and learning that ground the learning experiences found in the IM curriculum.
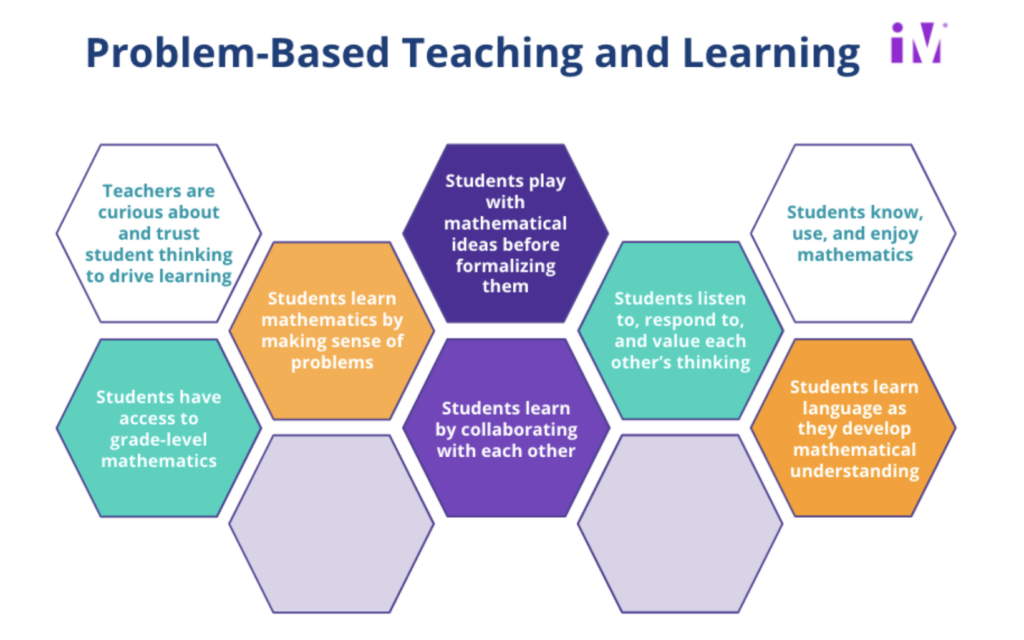
Teachers that are curious about and trust student thinking to drive learning will give students space to develop ideas. These students will play with mathematical ideas, and then move towards formalizing them. They will learn by collaborating with each other: listening to, responding to, and valuing each other’s thinking. As students are doing this hard work, their mathematical understandings are constantly developing. Hearing a question asked by another student or the teacher may cause them to reconsider their ideas. Listening to another student share their approach may inspire them to revise their reasoning or strategy.
One way this shows up in IM 6–12 Math™ is through Math Language Routine 3: Clarify, Critique, Correct. In this routine, students examine and analyze either a piece of individual student work or a common response or representation from the class. This piece of mathematical writing may be incorrect, incomplete, or ambiguous. Students first clarify what the author is trying to say, then consider how the writing can be improved upon. For example, students may replace vague words like “this” or “it” with specific language like “the equation that represents miles traveled per hour.” Students may also illuminate their own misconceptions, such as how to represent the output of a function after their peers share their reasoning on a graph, in words, and using function notation. Finally, the class writes a new response.
Through opportunities to play with mathematical ideas by talking and collaborating with each other, students are able to deepen their understandings in ways that lead to agency and ownership in their work. They gain tools for analyzing and strengthening their own writing moving forward.
Revision Supports Access for our English Learners
Teachers of English learners must hold high expectations for content learning by amplifying rather than simplifying students’ receptive and productive use of language. Some educators are tempted to reduce expectations to ensure “success,” simplifying the text that students need to read, or simplifying the written or verbal output that we expect students to produce. Instead, we should find as many ways as possible to present the learning goals in different ways. In English Learners, Academic Literacy, and Thinking, Pauline Gibbons describes this as “message abundancy.” We increase opportunities rather than narrowing them.
Math Language Routine 1: Stronger and Clearer Each Time provides English learners (and all students) with “message abundancy.” Students first write a first draft response, then engage in a series of structured pair meetings where they share, refine, and clarify their response through conversation. After their final pair meeting, students will have a response that is stronger and clearer than their initial draft. The teacher may also highlight particular language or key ideas that came up in students’ stronger and clearer drafts.
We see students reconsider and amend their responses that reflect feedback and learning from partners during the Stronger and Clearer Each Time routine. Through the repeated opportunities to share their ideas, hear other ideas, and be pressed for details or clarification, students have many chances to process and comprehend mathematical ideas. Not only are their responses stronger and clearer, but their understanding of that day’s learning goals is also stronger and clearer.
Revision is a Culturally Sustaining Practice
As teachers, we want to cultivate culturally sustaining practices that affirm all students as meaningful contributors within the classroom. While the word “revision” does not explicitly show up in Zaretta Hammond’s book Culturally Responsive Teaching and the Brain, I see elements of it in multiple places. Hammond writes that we need to “provide students authentic opportunities to process content,” which may include using methods from oral traditions. We are challenged to “reimagine the student and teacher relationship as a partnership” and “give students language to talk about their learning moves.”
In Math Language Routine 2: Collect and Display, the teacher circulates during work time and captures students’ verbal language and scribes it on the board. During the synthesis discussion, the teacher amplifies the words, phrases, and diagrams that they heard and saw students using. This provides an opportunity for students to process and clarify language and representations.This routine allows students to engage in authentic, organic conversation while the teacher captures thinking for the visual display. The partnership between teachers and students is strengthened when the students’ own words and ideas are used to drive the discussion. Students experience ownership of both their original ideas and the refined ideas that result after the discussion. As they replace familiar language like “plug it in” with more mathematical language like “substitute,” students build meta-awareness about how they talk and write about their mathematical ideas.
Conclusion
Revision plays so many important and nuanced roles in math class. Students deepen their conceptual understanding as they study their work, see their own ideas captured in writing, and change their minds many times during a peer discussion. They gain critical meta-cognitive skills that they can apply to challenging problems in the future. They experience recognizing and improving unclear communication within their own work, so that it becomes stronger and clearer.
What role does revision play in your classroom? How do you or will you intentionally build in opportunities for students to reconsider and amend their thinking, using peer or class discussion as a lens for revisiting their work? How might this impact how many students are able to be successful later in a cool-down or other formative assessment?
Learn more about the purpose and structure of the Math Language Routines here.
Citations
Jansen, Amanda. Rough Draft Thinking. Stenhouse, 2020.
