By Adrienne Baytops Paul, Math Specialist, UnboundEd, COO of My Mathematical Mind, and former Middle School Teacher
The 14 Practices of Peter Liljedahl’s Building Thinking Classrooms (BTC) complement the Illustrative Mathematics curriculum in remarkable ways. In my 23 years as a classroom teacher, I’d never previously witnessed anything like it. The practices align with IM’s problem-based instruction model, strengthening, guiding, and generating student thinking, while providing access to grade-level math content and rich mathematical tasks. In my final year in the classroom, I applied the 14 Practices to our de-tracking pre-algebra journey. Students experienced the flexibility and joy of mathematics through the probing questions of a first-rate curriculum and strengthened their confidence and conceptual knowledge through constant discourse and discovery. Although enacting the 14 Practices alongside IM implementation sounds ideal, questions may linger: How do I start? What does knowledge mobility look like? How can I monitor my students’ growth as the 14 Practices suggest?
Securing a Stress-Free Start
Cultivating Your Community to Prepare for the Shift
Non-curricular tasks were integral in our plan to prepare students for the shift in their mathematics learning experience. Toolkit #1 in Building Thinking Classrooms mirrored our goals to create a culture of learning in our pre-algebra class.
- Practice 1: What Types of Tasks We Use in a Thinking Classroom
- Practice 2: How We Form Collaborative Groups in a Thinking Classroom
- Practice 3: Where Students Work in a Thinking Classroom
We assigned non-curricular tasks to prepare our seventh-grade students for standing while working and collaborating nearly every day for the first two weeks of school. Unbeknownst to them at the time, all 65 students were experiencing elements of the Standards for Mathematical Practice on the first day of class! Because every student was standing, this posture automatically invited active student engagement in the lesson. They had so much fun learning, trying, debating, failing, and trying again! During our debriefs, we listened as students shared their experiences, mistakes, adjustments, successes, and failures. They were unaware of how much they were reaping the benefits of cooperative learning. We reinforced this regularly for the first two weeks, emphasizing how those moments of trial-and-error, analysis, and more would shape their learning in our thinking classroom.
Listening to and participating in the mathematical discussions provided windows into our students’ capabilities. These group activities created perfect opportunities to informally assess our new students’ levels of the following learner traits:
- conceptual understanding
- comfort level with mental math and computation
- risk-taking
- perseverance
- mimicking or stalling
Making space for student voice is an essential hallmark of the IM curriculum; through activities like the Math Language Routines, IM positions student voice as paramount to effective mathematical learning. Non-curricular tasks provided a stress-free space to model the curriculum’s expectations by requiring discourse that allowed students to gradually become accustomed to verbally justifying their solutions. Students could also practice the nuances of the 14 Practices without penalty. The intentionality of our tasks, student engagement, and subsequent discussions laid the groundwork for our collaborative learning environment.

Fully Invested in the Process
After nearly two weeks of non-curricular tasks, we introduced a curated version of Illustrative Mathematics’ seventh- and eighth-grade curricula. From our pre-assessment, we learned that students had varied exposure to math concepts (from content-forward exposure to ineptness with grade-level concepts), so we opted to include some eighth-grade concepts as extension tasks integrated into some lessons. At each grade level, IM provided tasks that adequately landed in the zone of proximal development for students to advance to a higher learning level with each lesson activity. We knew that IM’s curriculum gave students multiple entry points into the lessons, so students of all exposure levels could contribute to the learning. Each lesson’s design appealed to students because of the discovery-based problem-solving expectations and probing questions that were similar to those of the previously experienced non-curricular tasks.

Non-Curricular Practice Makes Perfect
Through our consistent use of IM, students learned that justifying their reasoning verbally in their triads was far more impactful than sitting in their seats and working individually. Having access to everyone’s responses on the vertical non-permanent surfaces helped us use evidence of student learning to elicit thinking, as described by NCTM’s eighth Mathematics Teaching Practice. It was another nuance that built agency, classroom culture, and trust. This also deepened understanding by giving students opportunities to observe and analyze multiple solution paths and decide which strategy aligned with their thinking or appealed to their logic. It far outweighed receiving a simple yes, no, check or “x” as feedback about misconceptions. It was differentiation in real-time.
One student shared his perspective with us, highlighting the advantages of working collaboratively:
“I love working in triads. Well, it’s much better than previous methods of learning that I’ve done in the past [where] it’s been like, teachers lecturing me…this year I get to do my own work and work with other people to try to figure out different ways of learning.
Like every day we have new people, and it’s nice to talk with different people about, like solving problems, you know. Sometimes we solve a problem but we have two different methods of doing it, so we can look at those methods and [learn] different ways of solving problems.”

In keeping with BTC Practice 6, When, Where, and How Tasks are Given in a Thinking Classroom, we required our students to stand or “Huddle up!” during the launch as they worked through instructional routines like “Which One Doesn’t Belong?” and “Notice/Wonder.” After reading the learning goals of the lessons and the launch, we asked “What do you think the lesson will be about?” or asked them to look for the connections between the launch and the forthcoming lesson to further analyze the task and its intent, piquing the students’ interest.
Trusting Student Collaboration
Learning by Listening
In Building Thinking Classrooms, Peter Liljedahl contends, “A thinking classroom is a classroom where students think independently and collectively.” Even before this book was published, the IM curriculum leveraged this statement’s truth by crafting tasks that invite both individual and collaborative learning to occur. The tasks regularly put the onus of the thinking on students, using prompts like “Explain,” “How do you know…,” and “Why do you think…,” which automatically remove the teacher’s ability to provide a singular, one-dimensional solution.
To amplify this type of mathematical thinking, we continued to use vertical non-permanent surfaces (Practice 3, Where Students Work). Seventh-grade students weren’t initially crazy about standing up in math class, but they got used to it! It was astounding to watch them work together, writing and explaining their thinking, and choosing the most efficient version of a solution. They were often confident enough to explain solutions in various ways by the time we would check in to hear their processes.
Learning by Looking
Just as it was described in BTC, students who were either stumped on a task or could confirm another group’s ideas took advantage of knowledge mobility. Once the students understood that they were not cheating when looking at someone else’s work, an even deeper level of mathematical discourse was ignited. Students’ confidence levels increased because their thinking was being highlighted and celebrated by their peers. One of the most meaningful ways to strengthen a community is to ensure everyone is valued and has something to contribute.
 .
. 
Learning Alone
Despite working in groups most of the time, there was no shortage of individual learning. Students met with us one-on-one to review concepts if necessary, and even during the triad work, individual processing occurred. I recorded one such instance: a group of three students was learning about solutions for systems of equations. All three were involved in the discussion, but I could tell one of them, “Student A,” was still uncertain. When I asked the group whether they understood the difference between the three solution types, they all said yes and Students B and C explained them.
Mrs. Paul: [To Student A], you don’t seem convinced.
Student A: I’m sure, I’m convinced. (I knew he wasn’t, however, so I stayed near the group. About 10 seconds passed, then Student A turned back toward me.]
Student A: So…if the graphs cross [he gestured], there’s one solution, if they never touch, there’s no common solution, and if the lines are the same, the answers are infinite, right?
Mrs. Paul: That’s right.
Student A: [Nods, then turns back to his group]
Student A had gleaned the concept from his partners’ drawings, collaborative learning, and took an additional moment to process and receive confirmation after he’d made sense of the concept in his own way. The BTC structure created this duality, this opportunity to consider the concept from his own perspective and his partners’ perspectives.
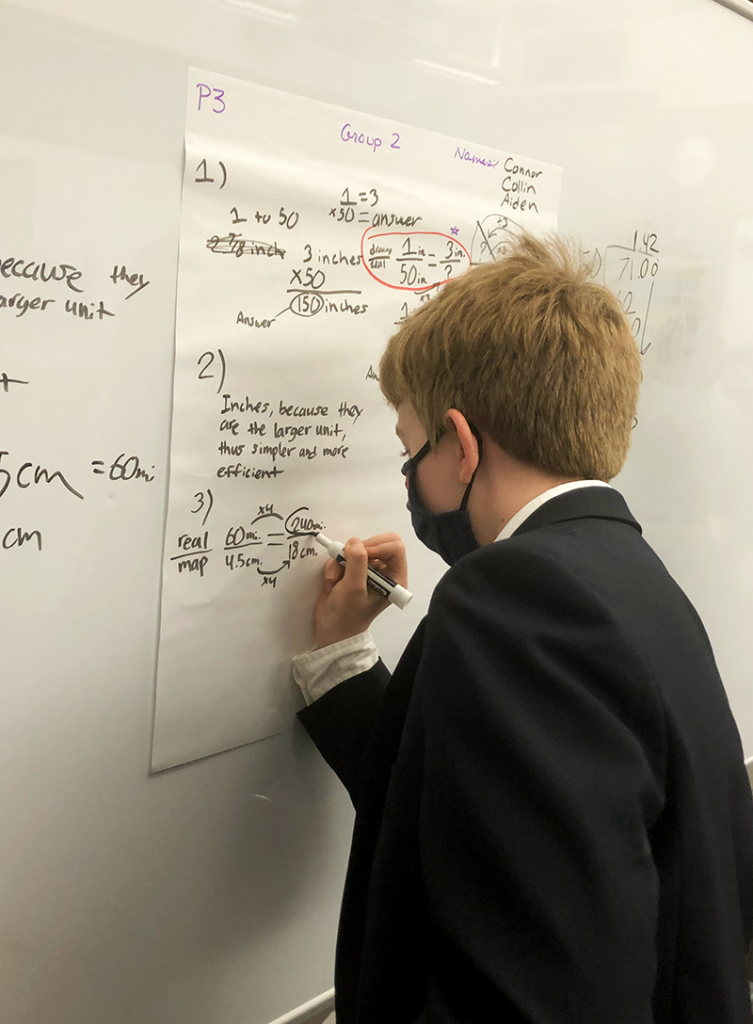
Evaluating What We Value
Grades that Represent Growth
Building Thinking Classrooms outlines many ways to evaluate student learning. There were several untraditional ways for our students to earn grades based on our agreement with the BTC text to evaluate what we valued. Students earned grades for attending to the following aspects of our class:
- maintaining participation points
- in-class assessment (ICA) grades
- unit test scores
- filling out their unit rubrics
- writing unit reflections
- completing unit test corrections
We took advantage of IM’s succinct and thorough seventh-grade curricular assessments and adjusted the tasks as necessary, since some of our curated lessons included content from multiple lessons. Because the students became used to articulating their reasoning, it became habitual for them to explain their thinking on their written assignments, even if we didn’t remember to require it! The impact of the collaborative learning environment and the IM curriculum asking such questions as “Explain how you know whether the slope is positive or negative,” or “What do the equations of the proportional relationship have in common?” was especially evident when a student referenced a classmate’s perspective when explaining an answer on an assessment.
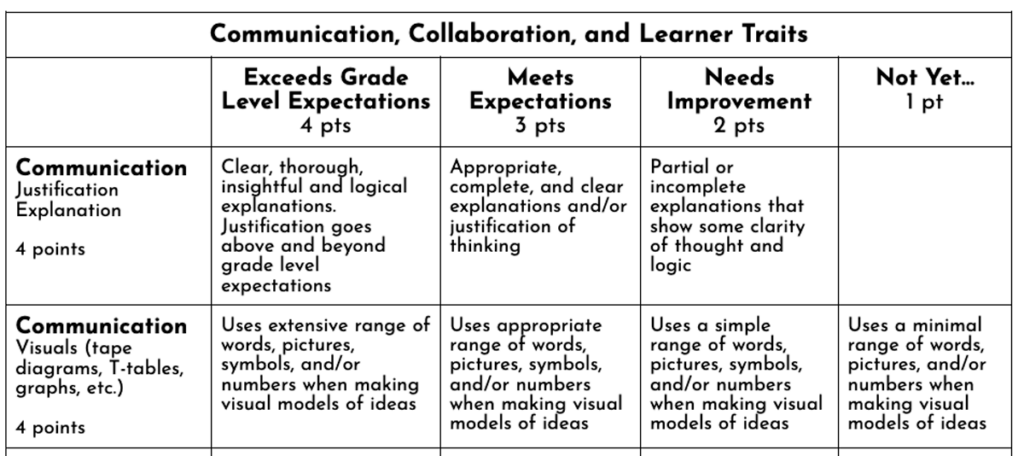
Rubrics for Review
We required students to hand in their completed rubrics and reflections. The rubric’s front side was composed of IM’s curricular learning targets of the unit derived from the standards, and the students placed checkmarks on the categories that indicated their perceived comfort level with the concepts. The backside was a rubric of “Communication, Collaboration, and Learner Traits.” It was here that students had another chance to self-reflect on their behavior and interactions as learners.
Writing Reflections in Math Class
Our students also wrote detailed reflections about their overall performances for nearly every unit of study. We would read the reflections, provide specific feedback, ask students to refer to them throughout the units, and reference them during our individual student meetings. This level of engagement built a robust trust between us and the students; they knew how much we believed in them, how this new approach was impacting their understanding, and how much growth they had experienced from month to month.
It’s Time
The Illustrative Mathematics curriculum and the 14 Practices of Building Thinking Classrooms feel very much like the change that mathematics education so desperately needs right now. Many of our previous practices are dated and ineffective; the days of algorithm memorization and lecturing in math class should be practices of the past. I will continue sharing this experience with math educators because I believe that deeply in this remarkable curriculum and these groundbreaking instructional practices. Shifting your mindset from “The students can’t do this…” to “How can I help them do this?” and putting the time into creating opportunities for students to cooperate and make sense of mathematics can empower both you and your students.
 Adrienne Baytops Paul
Adrienne Baytops Paul
Math Specialist, UnboundEd, COO of My Mathematical Mind, and former Middle School Teacher
Adrienne Baytops-Paul has been an educator for over two decades and has always sought to provide children with informative, engaging, and effective learning experiences. Adrienne has taught math at both the elementary and middle school levels. As a seventh-grade math teacher, she worked to de-track pre-algebra in order to provide high-quality and equitable mathematics learning opportunities for all of her students. She regularly writes about mathematics instruction, standards, and best practices and has had her research published in the Journal of Mathematics and Science.
At UnboundEd, she creates mathematics professional development content. Adrienne is the Chief Operating Officer of My Mathematical Mind, a mathematics education consulting firm, through which she conducts professional development for math educators and administrators around the country.
