By Brea Jimenez, Specialist, Facilitator Certification and Quality Assurance and
April Mouton, Senior Director, Access, Content & Equity
Special education is intended to provide bridges between challenges and triumphs for students with exceptionalities.
“I look back fondly on my memories as a brand new special education teacher looking around my empty classroom and wondering when my perfectly laminated name cards, interactive calendars, and labeled task bins would be delivered. When the delivery never came, I quickly learned just how many of those bridges come out of the minds and hands of the brilliant special educators I respect and admire. I am grateful to be a part of the education specialist community and have had the immense privilege of working with students with severe disabilities in a variety of settings. I am always excited to speak on how students with disabilities can do anything with the right bridge and give knowledge back to the community that has poured so generously into my own learning. I am delighted to collaborate on part 3 of this blog to provide our community with strategies and examples from IM K-5 Math to support students with moderate to severe disabilities and to contribute toward a world where all learners know, use, and enjoy mathematics.” – Brea
Click here to read Part 1 of this series.
Click here to read Part 2 of this series.
Illustrative Mathematics K–5 Math is a high-quality, standards-aligned, problem-based core curriculum that enriches learning environments and reduces barriers of access through the UDL-framework and invitational approaches. While it is not intended, designed, or recommended to be used as an academic intervention or as a replacement for specialized academic instruction, students receiving intensive academic supports may still benefit from IM’s diverse representations, predictable structure, and real-world connections (Belland et al., 2006). In addition to accommodations, supports, and interventions deemed appropriate by the Local Education Agency (LEA) and Individualized Education Program (IEP) team, IM can provide effective supplementary materials and routines to further enrich and diversify specialized academic programs. Ultimately, the IEP team and LEA know their student population’s educational needs better than any curricula and will need to determine the extent to which IM K–5 Math should be used in populations of students with intensive academic supports. The information provided here is only intended as a helpful guide for where to begin integrating IM in self-contained classroom settings.
Routines, centers, and representations provide invitational access points for students, increase mathematical interpretation, and cultivate discussion-rich learning experiences. This blog will cover three key considerations in successfully integrating routines, centers, and representations from IM K–5 Math into intensive academic support and self-contained classroom settings.
I. Routines
In IM K–5 Math, routines can refer to either Math Language Routines (MLRs) or Math Warm-Up Routines. In this section, we will discuss how both can be useful supplementary tools to a specialized academic math program. There are eight Math Language Routines. While they are all beneficial and could be integrated into any program, we will focus on “Three Reads.”
A. Math Language Routines: Three Reads
Three Reads supports students in reading and interpreting a mathematical text, situation, diagram, or graph three times, each with a particular focus. This routine is designed to support task analysis, a widely-accepted practice for students with significant exceptionalities , which breaks down a task or activity into manageable steps. While all students may benefit from some degree of task analysis (whether self or teacher-directed), it is extremely useful for building procedural and conceptual processing skills in students with cognitive disabilities (Spooner et al., 2019). Three Reads captures the essence of this kind of task analysis in a simpler form: exploration analysis. While exploration may be a natural process that does not require support for many students, others may not be able to explore independently. Let’s explore how a modified version of Three Reads could be used to support a student named Shayne as he explores solving all kinds of problems involving fractions.
Example:
Shayne is a fourth-grade student with significant cognitive disabilities who is working on a math problem in a self-contained classroom with specialized academic instruction. The problem is as follows:
Jada and Noah’s class are hiking at a park. Here is a map of the trails. The length of each trail is shown:
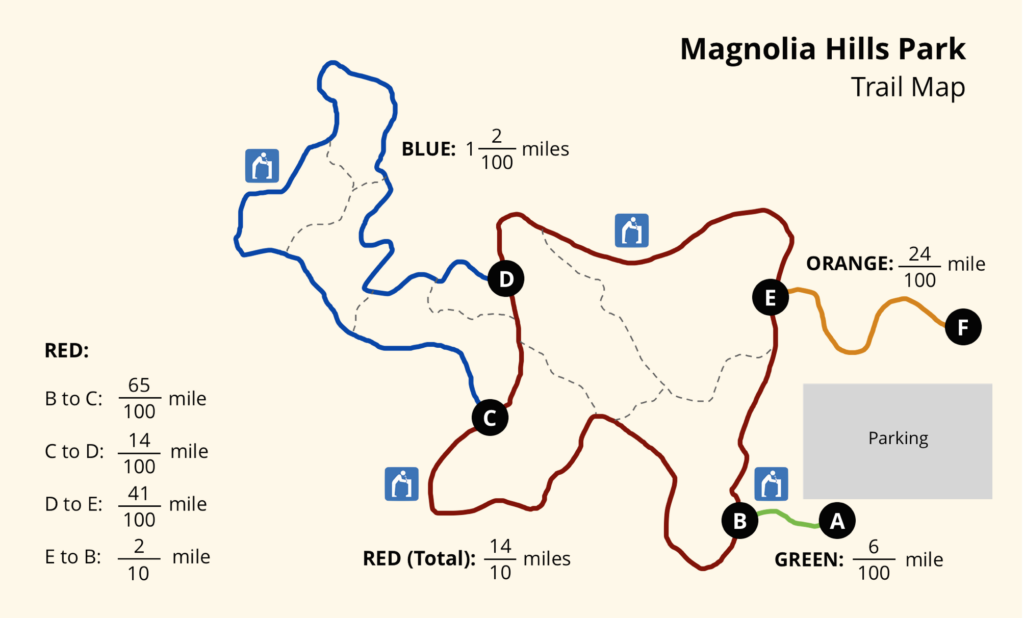
Following the first read, Shayne and his teacher discuss what the story is about. Then the teacher covers the numbers in the problem and prompts Shayne with the following:
“Touch F, now touch E—what color is that path?”
“Which letters are on the green path?”
“Trace the red and as you pass each letter, say it aloud.”
“What do you think these paths are for?”
Following the second read, Shayne’s teacher underlines each color word with the appropriate color (i.e. red line under Red (Total)) and uncovers the associated fractions. Shayne’s teacher then asks the following questions/gives the following directions and repeats them for each path color:
“Look at the orange path. This orange line shows us which fraction goes with the orange path. What is the fraction that goes with the orange path? Write that fraction with the orange marker.”
“What fraction would we write with the green marker?”
“What other color paths also have fractions?”
Following the third read, Shayne’s teacher reviews a model for adding fractions, which may be a model Shayne and his teacher made together or a version of an anchor chart from classroom instruction. Shayne’s teacher then asks the following questions:
“Which two colors would you like to walk around? Does that seem like a long walk or a short walk?”
“If I wanted to take a long walk around all the paths, could I figure out how far I am going by adding? How?”
Shayne may need a varying degree of prompting and support to interact with this activity. However, using the Three Reads math language routine provides an opportunity for Shayne to internalize the necessary information, receive scaffolding for his exploration, and engage in his modeling of the solution steps for this type of problem.
Take Time to Reflect
Are there students you support that could benefit from the Three Reads math language routine?
In what new ways can the students you support explore math and make their thinking visible?
II. Math Warm-Up Routines
IM Math warm-up routines are intentionally designed to elicit student discussions around the mathematical goal of the lesson and to support the development of student thinking and precision with language. For students with exceptionalities, their intellectual disabilities are often not their only barrier to learning. Students may have comorbidities to consider that impact their gross and fine motor capabilities, hearing or vision impairments, and more. The routines in IM Math take into account all the additional barriers students may have when initially accessing the activity. These routines are wonderful vessels for the unique style of differentiation students with significant exceptionalities need.
For a spotlight routine, we will look deeper at “What Do You Know About ______.”
- Math Warm-Up Routines: What Do You Know About _____?
This routine uncovers students’ ideas of numbers, place value, operations, and groupings through visuals of quantity, expressions, and other representations. It invites students to consider where they see numbers embedded in various contexts or how they compare and order numbers. While it was designed to include verbal language, students are ultimately given the chance to respond in the ways they are able. For some students, this may be done with alternative and augmentative communication (AAC) devices or with interpreters. With other students, this may be done with visual representations. However a student is able to engage with the warm-up, the goal is the same: to invite the student into the math. Let’s explore how “What Do You Know About _____” could be used to support a student named Kasim as he explores learning more about rectangles and squares.
Example:
Kasim is a fifth-grade student with significant cognitive disabilities. He is also learning English as a second language and has limited verbal communication. He is beginning math instructional time in a self-contained classroom with specialized academic instruction and structured English immersion. The lesson for the day focuses on identifying and classifying quadrilaterals. The warm-up is as follows:

Kasim’s teacher reads the question to the entire class and then sends students to their working small groups to receive their individualized accommodations. While working with Kasim, the teacher points to the shape in front of him and prompts him for the name of the shape. He states “square.” The teacher affirms “Yes! A square.” and hands Kasim a variety of crayons and prompts him to draw on the same paper as the square with the prompt “What do you know about squares? Show me.”
Kasim begins drawing around the shape, adding colors and doodles until he places the crayons down. The teacher returns to ask questions about the drawing he has made. “What is this?” The teacher points to a shape above the square. Kasim responds “house.” His teacher affirms this response as well. “Yes! A square does kind of look like a house.” The teacher repeats this with a rhombus, rectangle, and trapezoid. Kasim’s teacher uses these drawings to create anchor charts for him labeled with each shape. The one they created for the square includes Kasim’s drawing of the house.
Kasim may continue to need a varying degree of prompting and support to interact with future activities concerning classifying or comparing quadrilaterals. However, the use and adaptation of the “What Do You Know About ____” math warm-up routine provides an opportunity for him to internalize the necessary information, receive scaffolding for the exploration, and engage in the creation of learning materials that are meaningful to him. As they move into more difficult instruction, Kasim and his teacher will benefit from the learning explored in this warm-up routine.
Take Time to Reflect
Are there students you support that can benefit from the “What Do You Know About ___?” instructional routine? In what other ways can you envision students interacting with this routine?
III. Centers
Centers can be a powerful strategy to support students with exceptionalities in self-contained settings because of their skill repetition and predictability. In special education, repetition can be useful for globalizing skills, particularly in populations with Autism Spectrum Disorder (King et al., 2016). Centers provide opportunities where students can practice the same skills in different applications. This can help students practice key skills while still promoting flexibility and generalization.
For a deeper discussion and some examples of how centers can support this learning, we will focus on the center “Grab and Count (K–1).” In this center, students grab a handful of pattern blocks (or other objects), guess how many they have, and then count how many they have to verify their predictions. With many kindergarten and first-grade students, this activity could be done at a table with a peer, and they may even record their own guesses and counts. For other students, this center may be integrated through other aspects of the classroom to support their generalization of the skill. For example, let’s look at how a teacher, Mr. Jackson, integrates the Grab and Count center into his self-contained K–2 classroom.
Context: Mr. Jackson teaches a K–2 self-contained special education classroom. His district uses IM K–5 Math, but his special education department uses a different core curriculum for exceptional students in self-contained settings. Mr. Jackson uses some of the IM K–5 Math materials he has access to in his classroom with the guidance of both the general education and exceptional children’s curriculum coaches. He has created a center station for his students and they self-select centers when given tokens.
Mr. Jackson gives two students a green token. They select from three different matching green centers. Today they chose Grab and Count. The two students take the materials to a green table and unpack the materials. Inside the tub is an empty bowl and a “help” icon card. The students take the help icon to their teacher, and he joins them at the table with manipulatives of various sizes. Mr. Jackson curates the centers in this way with tubs and intentionally empty bowls so his students can interact with the center independently, similar to their grade-level peers.
Mr. Jackson prompts his students to select the first item they will count (small rubber ducks) and holds the bowl out without verbal prompting. The first student grabs a handful of the ducks. Mr. Jackson pulls out a card with visual cues for guessing and asks, “How many?” The student quickly answers, “Five!” Mr. Jackson prompts, “That is a good guess. Can you count how many?” The student starts counting. Mr. Jackson prompts for a second trial, and says “How many? Count with me!” He proceeds to take one duck out of the hand while saying each number name. Mr. Jackson prompts again once the counting has concluded, “How many?” The student answers correctly, “Four.” They continue until the time for this center has concluded.
After a transition to snack time, Mr. Jackson asks the same students from his Grab and Count center to grab some crackers out of their cups. He prompts, “How many?” and walks the students through the same prompts as the center. Rather than count with them by removing the crackers, he allows them to eat the crackers as they count.
Mr. Jackson’s globalized approach and use of this center provides his students with higher-quality repetition tasks. The students can globalize this request and explore a variety of strategies to support their meaning-making, 1:1 correspondence, and overall tolerance of the activity.
IV. Representations
The IM curriculum includes mathematical representations that are designed to be used for two main purposes: to help students develop an understanding of mathematical concepts and procedures and to help them solve problems. The materials make thoughtful use of representations in both ways. These representations can be used for this purpose in any math community. For students with exceptionalities, representations can be especially helpful when they have cross-curricular and interdisciplinary functions. To highlight an example of this we will look deeper at connecting cubes.

A. Connecting Cubes
A teacher named Coach Harris uses connecting cubes for mathematics but wanted to integrate this representation across subjects for students to build familiarity and connect similar concepts. Coach Harris would also like to increase students’ positive associations with activities requiring 1:1 correspondence and wants to avoid connecting cubes becoming a trigger for students if they only appear during math instruction. Here are some ways Coach Harris integrates this representation across subjects in a self-contained special education class:
Example 1 in mathematics: Students can use colored cubes for addition and subtraction tasks. Students can even use two different colors to represent the two addends or the minuend. Students can use all connecting sides to create geometric shapes. Students can recreate 2D shapes.
Example 2 in English language arts: Students can use color cubes to represent the consonants and vowels in words. Students can use familiar CVC or CVCe endings and add cubes with letters to the beginning to create new words. Students can use cubes with letters written on them to create their names, addresses, or days of the week. Students can use connecting cubes to discuss prepositions and sentence structures in language.
Example 3 in social studies: Students can use multicolor cubes to represent cardinal directions. Students can use cubes to vote on rules and classroom norms. Students earn cubes in the classroom economy by completing a classroom job and using them to “buy” activities and sensory toys.
Coach Harris recently used the connecting cubes during a playtime activity, instructing the students to showcase how tall they thought their teacher was using the cubes. Coach Harris then stood each tower up to showcase how close or far they were from the actual height. As a part of their math instruction that same day, students then counted how many they were over or under in their estimation (CCSS.3.MD.B.3; CCC.3.DPS.1.g1).
During an assessment, connecting cubes were allowed to be used to support independent problem-solving. When a question regarding units of measurement was asked, many of Coach Harris’s students requested the connecting cubes, connecting them to prior learning. By providing multiple opportunities for students to represent, measure, and explore the physical space with cubes, Coach Harris’s students have more opportunities to generalize the skill, scaffold their own instruction, and become confident mathematical thinkers when using this representation.
Conclusion
Since many education specialists are working across multiple grades, different grade levels were intentionally included in this blog to reflect that experience. While the IEP team and LEA will ultimately determine the extent to which IM K–5 Math should be used with their student populations, there is no shortage of opportunities to integrate some of the IM curriculum activities and frameworks into a self-contained setting. IM aims to foster and participate in a world where all learners know, use, and enjoy mathematics and does not fixate on an all-or-nothing approach for special educators. Playful mathematical exploration and framing the student as the doer of mathematics can be beneficial to any population. We hope this blog series has expanded and refreshed thinking when it comes to the IM Classroom and students with exceptionalities. Regardless of the approach a site or district may take with instructional materials or curriculum for their special populations, we are encouraged and honored to be a part of the conversations on ensuring meaningful and equitable access to problem-based, grade-level instruction.
References:
Belland, B. R. , Ertmer, P. A. , & Simons, K. D. (2006). Perceptions of the Value of Problem-based Learning among Students with Special Needs and Their Teachers. Interdisciplinary Journal of Problem-Based Learning, 1(2). Available at: https://doi.org/10.7771/1541-5015.1024
King, Seth A., Christopher J. Lemons, and Kimberly A. Davidson. “Math interventions for students with autism spectrum disorder: A best-evidence synthesis.” Exceptional Children 82, no. 4 (2016): 443-462.
Spooner, F., Root, J. R., Saunders, A. F., & Browder, D. M. (2019). An updated evidence-based practice review on teaching mathematics to students with moderate and severe developmental disabilities. Remedial and Special Education, 40(3), 150–165. https://doi.org/10.1177/0741932517751055
 April Mouton
April Mouton
Senior Director, Access, Content & Equity
April J. Mouton (she/her/sis) received a BA in political science and minors in mathematics and African studies from the University of California, Davis. She received her MEd in counseling education, K-8, administrative, and pupil personnel credentials from San José State University. She has served as a mathematics and cultural studies teacher, administrator, and consultant for 22 years. April is currently the senior director of access, content, and equity at IM and a doctoral candidate at Texas State, with a focus on demystifying mental health, culturally responsive teaching, identity formation curriculum integration, leveraging ancestral knowledge, and equity forward systems. She is the mother of three dynamic children, and her husband is a writer and educator.
 Brea Jimenez
Brea Jimenez
Specialist, Facilitator Certification and Quality Assurance
Brea J. Jimenez (she/her/hers) received a BA in English from Ottawa University in Ottawa, Kansas. She received an MA in Special Education from the California State University of Bakersfield. She is dual-certified in K–12 moderate to severe special education (exceptional children) and early childhood special education. She holds authorizations for English learners and autism populations. She has spent her classroom and administrative career working with Pre-K to 22-year-old students with exceptionalities in a wide variety of inclusion, self-contained, and transition settings. Brea is currently the facilitator certification and quality assurance specialist at IM. She has a passion for universally accessible classroom design and empowering all learners to have agency over their educational experiences. She is a zealous knitter, the mother of two children and two cats, and proud partner to a US Navy Veteran.
