By Jen Hawkins, IM Certified® Facilitator and Independent Curriculum Implementation Specialist
As I sat at the table in the back of the room, I watched the teacher reveal an image connected to the lesson’s warm-up. She told her students they would have a minute to consider the image, and then she would ask them about their thinking. Her students gave a thumbs-up when they had an idea to share. After waiting a true minute, she selected a student to share their idea about the image.
She wrote down a couple of words that the first student said. Faces brightened. Eyes lit up. The students’ excited expressions revealed what they were thinking: “The teacher thought this was something interesting! Maybe even something important!”
The teacher called on another student who was waiting expectantly with a thumbs-up signal. She circled the part of the image that the student referred to, and the student smiled broadly. Students on the carpet looked eager to join the mathematical discourse happening around them. I could tell students’ ideas were acknowledged and appreciated in this classroom. I was observing a vibrant, thinking math community.
Annotate & Acknowledge
How you launch math class matters. Starting an Illustrative Mathematics lesson with all students engaged and tuned into the same image, expression, or equation promotes a thriving math community.
We want students to feel secure and begin class from a place of assurance. Listening to all ideas and accepting them without evaluation encourages curiosity and fosters the confidence students need to examine images and representations throughout the entire lesson. According to the National Research Council (2001), “Because of the abstract nature of mathematics, people have access to mathematical ideas only through the representations of those ideas.” Students need to experience varied representations regularly and connect them to mathematical ideas in order to solidify their understanding.
A teacher can use the launch to pique students’ interest in the upcoming math topic and explore new vocabulary as it comes up naturally in discourse. Annotating allows students to see mathematics become visible as a classmate speaks. Ideas transform into images and representations, and they become accessible knowledge for all members of the classroom. “Visual representations are of particular importance in the mathematics classroom, helping students to advance their understanding of mathematical concepts and procedures, make sense of problems, and engage in mathematical discourse.” (Arcavi 2003; Stylianou and Silver 2004). Additionally, “Math drawings and other visual supports are of particular importance for English language learners, learners with special needs, or struggling learners, because they allow more students to participate meaningfully in the mathematical discourse in the classroom.” (Fuson and Murata 2007)
For these reasons, I suggest teachers begin class with one image that all students can see comfortably. Looking at a common image strengthens the classroom community, whereas looking at images independently can cause students to lose focus.
The IM curriculum uses warm-ups to launch lessons and invite students into the mathematics (More about IM warm-up routines). In each of these routines, the teacher notes succinctly state:
- Display the image.
- Give one minute of quiet think time.
- Share and record responses.
These short, bulleted notes are so much more than teacher directions. The practice of annotating a mathematical image, equation, or expression as students share their ideas seems like a simple act, but there is much more going on than meets the eye. Principles to Actions, an influential mathematics publication, notes that it is imperative to “elicit, value, and celebrate varied approaches and solution paths…” while annotating and acknowledging student ideas. It describes the importance of developing “…environments in which students feel safe to engage with one another and with teachers.” To create this kind of rich, productive community, teachers must be intentional with their annotation process.
Some examples of the decisions to make:
- What will I write down?
Be selective and choose the right words to capture in your annotations. The example below shows how a student may respond to a question comparing corn and broccoli in a bar graph. The purple teacher notes focus on the important mathematical aspects of the student’s reply. “Teachers must determine how to build on and honor student thinking while ensuring that the mathematical ideas at the heart of the lesson remain prominent in class discussions.” (Engle and Contant 2002)
- What should I do when a student shares an inaccurate idea?
Research tells us that “…it is critical not to evaluate their statements so you can hear from as many students as possible. Many students will not risk sharing their statements if they feel they will immediately be critiqued.” (Seda and Brown 2021) This means that even if a student says something incorrect, criticism should not be our first response. Instead, it can be an opportunity for deeper exploration. For example, a student saying “All rectangles are squares,”’ when the inverse is true can be a tricky situation to navigate. We want the student to feel valued even if the response is inaccurate, yet we must provide accurate mathematical information. An incorrect comment might be navigated by writing down the student’s statement and eliciting different ideas from other students. Classroom discourse involves disagreement at times. Students in a strong math community are taught to respectfully disagree and think together to come to consensus. We can anticipate that another student will say the correct converse, “All squares are rectangles.” The teacher has an opportunity to talk about how the characteristics of squares and rectangles can help us figure out which statement is true. Student thinking can be solicited, and a brief discussion of the shapes’ features can lead to the conclusion that the latter statement is true. The teacher can wrap this up by circling or highlighting the correct statement. Then, she might mention that math ideas can be tough to decipher at times, but an organized consideration of thoughts can help us get the shapes figured out correctly. This modeling will help students become analytical thinkers. “When teachers allow students to share their thinking with others, it contributes to students’ confidence in their own ability to reason.” (Seda and Brown 2021) - Where will we experience the warm-up?
Options include at desks, standing in a math huddle, or sitting on the carpet. It is important to consider the ages of your students, the time of day, and the classroom configuration when making this decision. Try out various ideas and take note of what works best for your students. - How will I know students are ready to share?
Hand raising has traditionally been a classroom signal, yet research shows it often makes reluctant students cease thinking. In an IM math community, a quiet signal is best to indicate that you have an idea to share. Some students may give a thumbs-up or put up an additional finger or two to indicate they have more than one comment to make. - What sort of markers do I need?
Bold, thick markers are encouraged to annotate as students talk. The use of a thick marker means that the writing is visible to all. I suggest using color freely. It may also help to change colors with each speaker or to use similar colors for similar ideas. An example of the impact of using color is shown in the sample below: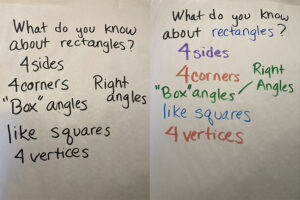
- What should I do if many students have the same thoughts or answer or reply?
Using an underlining method can show that multiple students have the same thought. If ten students think the value of an expression is 7 and two students think it is 8 my annotations might look something like this:
The repeated lines under the proposed answers acknowledge every student in the class.
- Should I put student names with their thoughts?
As a general practice, writing student names with ideas is not recommended as it is time-consuming and could be distracting. However, there are times when it may be the best thing to do. If a student thinks of a way to solve a problem that is novel to the group, calling that method “Jarod’s Way” might help students remember the method, and it will undoubtedly make Jarod feel proud of his thinking. Knowing when a student needs a boost and using their contribution as an opportunity to put their name next to their thinking is a small teacher move that can go a long way toward encouraging student participation. - Where should I annotate?
Options include chart paper or on a white board. Large chart paper is best to create an anchor chart that students can refer back to during the lesson or throughout a unit. A whiteboard will be best if the notes will not be needed for reference later.
Conclusion
The start of math class is an important time for building students’ confidence and priming them for learning. The warm-up that kicks off a lesson is an opportunity to set the tone, engage all, and instill pride and ownership among students. It’s not a two-way conversation. Instead, it’s a whole-class learning experience where we want all students to feel like a valuable member of the collective discussion. This is important because “…acknowledging student contributions, and attending to culture and language play substantial roles in equalizing mathematics gains between poor and non-poor students.” (Battey 2013; Cross et al. 2012; Krisker et al. 2012; Robinson 2013)
Annotation shows our students that we care about their ideas and that we want to know what they think. It also shows that we care about them as people. In a vibrant, thinking math learning community all contributions are valued. By writing at least one aspect of a student’s thinking, we show that we respect their minds and feelings. When students feel heard, they feel good about themselves. When we listen and annotate, the goal of the launch has been reached. Students are interested, confident, and ready to learn.
Next Steps
After a lesson, consider the following to reflect and grow:
- Did I acknowledge all the contributions made to the launch today?
- Could I have used color in a different way?
- What would I change in the future if I were to launch this lesson again?
- Who didn’t contribute that I might seek out and encourage tomorrow?
 Jen Hawkins
Jen Hawkins
IM Certified® Facilitator and Independent Curriculum Implementation Specialist
Jen Hawkins is a math consultant and facilitator for Illustrative Mathematics. She has a BA in elementary education with a concentration in mathematics and an MA from Mount Holyoke College in teaching mathematics. She has worked as a teacher and as a math coach in schools in both the Caribbean and Massachusetts. For a number of years, she left the classroom to focus on assessment and worked on the Massachusetts Mathematics MCAS test. She believes mathematics is the language of quantity and shape that everyone can appreciate and understand with the right resources and support.
