By Joseph Koelsch, IM Certified® Facilitator
“I’ve said it before: equations are the devil’s sentences. The worst one is that quadratic equation, an infernal salad of numbers, letters, and symbols.”
– Stephen Colbert
Did you ever feel the same way? I know that I felt that way when I was a student. Even well into my teaching career, I viewed quadratics as an exercise in persistence, testing students’ abilities to deal with challenge, abstraction, and uncertainty. It was a gateway we all had to get through in order to prove that we were worthy. That all changed for me last year when I first taught quadratic functions using Unit 6 in the IM Algebra I course. I found myself seeing quadratics in a whole new light, which reframed how I thought of all of mathematics.
I didn’t always think of math as an ordeal. Up through grade 7, math made sense. I understood the concepts in a logical sense—I knew how it worked—and in a practical sense, I could see why it was useful. I loved math and was good at it.
Regrettably, starting in grade 8, understanding no longer seemed as important as getting the right answer. I did what the teacher said to do, which led me to the desired solutions, but I had no idea why the steps worked or why the work mattered. In Algebra 1, I could factor one quadratic expression after another and “FOIL” my way through any pair of binomials. I couldn’t say, however, what made an expression like $x^2+11x+24$ “quadratic” or what it was for.
When I became a teacher, I started to question my teachers. Why hadn’t they done more to make math meaningful to their students? Over time, I gained a clearer perspective: the traditional math instruction I received was a holdover from the manufacturing age. It was meant to create calculators, not sense makers.
That is why I love IM K-12 Math™, especially Unit 6 in the Algebra 1 curriculum: “Introduction to Quadratic Functions.” In this unit, students are invited to explore quadratics’ unique structures, patterns, and uses before ever being asked to factor or multiply expressions. The emphasis is on understanding these patterns and relationships intimately before ever being asked to manipulate or solve equations.
Unit 6, Section A: A Different Type of Change
The unit opens with a lesson called “A Different Type of Change,” and from the very first activity in this lesson, it’s clear that students will be approaching quadratics differently than in the traditional class. The first activity is a “Notice and Wonder” in which three tables of values are presented to students: two that are familiar and one that is novel.
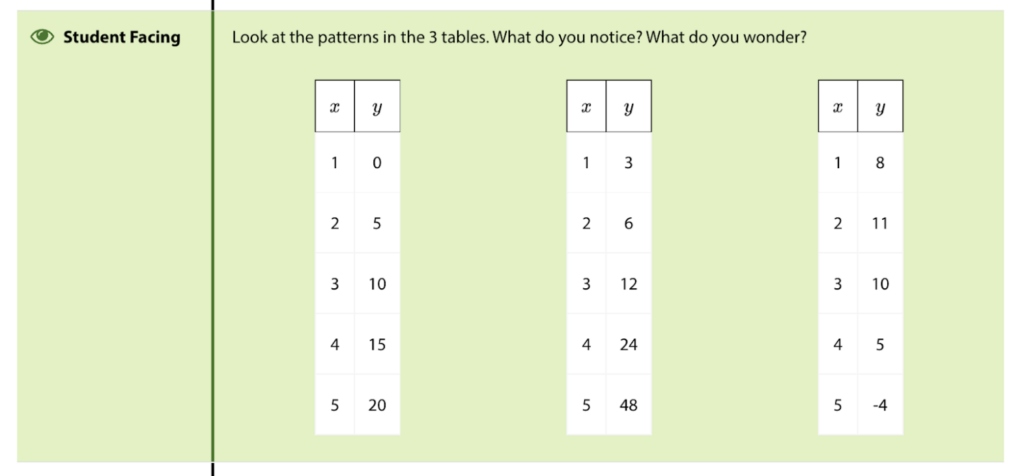
Students are not asked to fill in the table, nor are they asked to create an equation that would represent the relationships in the table. They are simply asked to notice and to wonder. By removing the pressure of a right or wrong answer, students are free to be curious about the relationship in the last table and to observe that it is distinct from the linear and exponential relationships in the first two tables.
Unit 6, Section B: Quadratic Functions
Throughout the first two lessons of the unit, students are invited to explore quadratics not as equations but as a pattern. In Lessons 3 and 4, students expand their exploration of quadratics to include geometric patterns while further comparing these patterns to the familiar exponentials.
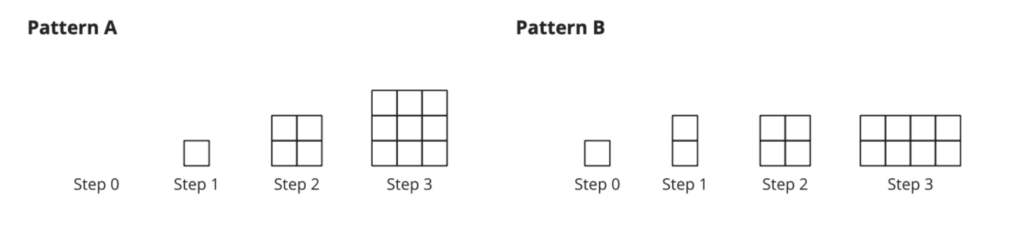
For the full task, view: https://im.kendallhunt.com/HS/teachers/1/6/4/index.html
Much like the opening activity in Lesson 1, this activity invites students to engage with new content through multiple entry points. All students can engage in this task by drawing or extending the pattern of growth. This task also invites students to look for and make use of structure. It would be unwieldy to draw Step 18, and so creating an equation or noticing a pattern can make the work easier. I also love this activity because it reinforces the reason that we call an object raised to the second power “squared.” Students can literally see that there is a growing square in this geometric pattern, and they make the connection that this square can be represented by a variable to second degree. Thus, they construct their own definition of a quadratic.
In the next few lessons of this section, students are invited to use this new idea to model situations from the real world. In Lessons 5 and 6, students look at how quadratic expressions can be used to represent the distance-time relationship in objects that are falling from the sky or are launched into the air.
For instance, students analyze the heights of a launched cannonball over time, comparing them in two situations.
Ignoring gravity:

Accounting for gravity:

Upon graphing and writing an equation for each function, students observe that one is linear and the other quadratic.
It wasn’t until I taught using IM K–12 Math that I realized that the rate at which an object accelerates toward the ground can be represented by a quadratic equation. Now, the connection between quadratics and gravity is one of my favorite things to teach, because it is one of the first times that students begin to understand that our universe is in large part governed by and can be understood through mathematics. It is thrilling for students to recognize that they can predict when an object will hit the ground using an equation that they understand and can work with.
Students also interact with quadratic functions outside of the context of physics. In Lesson 7, students explore the economics of pricing and its impact on revenue. They begin to see mathematically what they may know to be true intuitively, that if a company charges more money for a product, then they will make more money…to a point. After that point, fewer people will buy the product, and the company will begin to make less money. Through these explorations, students see that mathematics can help them better understand how things work in their world, that it has relevance.
For seven full lessons, students are invited to explore a “different kind of change.” They see the patterns, both numeric and geometric, and phenomena that can be described with quadratic functions and they connect them to real-world lived experiences. These lessons allow students to first build their intuition about quadratic relationships in more concrete ways—through visual and applied contexts—rather than diving right into their abstract representations. This means that when students begin to work with the quadratic equations in standard and factored form in Section C, they have a concrete foundation on which to build their understanding. Then, in Section D, as students connect quadratic equations to graphs, they can think about real-world examples to more fully understand the graphs’ features. Finally, in Unit 7, when they solve quadratic equations, students already have a conceptual framework to help make sense of this process on a deep and logical level.
Next Steps
Looking back, I can’t help but wonder, if IM K–12 Math had been around when I was a student, how my mathematical journey might have been different. If I had been trusted to explore and understand quadratic relationships before being asked to manipulate and solve abstract equations, I might have felt more at ease and less threatened by the content. Might this understanding have built my confidence and unlocked understanding in later classes? Unfortunately for me, I’ll never know the answer, but for my students and yours, hopefully, it’s a question they’ll never have to ask.
