By Max Ray-Riek, Senior Director, Teacher Professional Learning
Our vision at IM is a world where all students know, use, and enjoy mathematics. Educators in our IM Community work toward this vision in classrooms day after day using our problem-based curriculum. What does an IM classroom look like? What does it sound like? We often get asked these questions, and one way we share the story of an IM classroom is through the elements of problem-based teaching and learning.
(If the Instagram preview is not loading below, please refresh the page.)
View this post on Instagram
You may have seen these “hexagons” before–in an IM booth, at a conference session, during a professional learning session, on a sticker, or in a social media post. Even if you’ve seen them before, take just a moment to look at them closely.
What do you notice? What do you wonder?
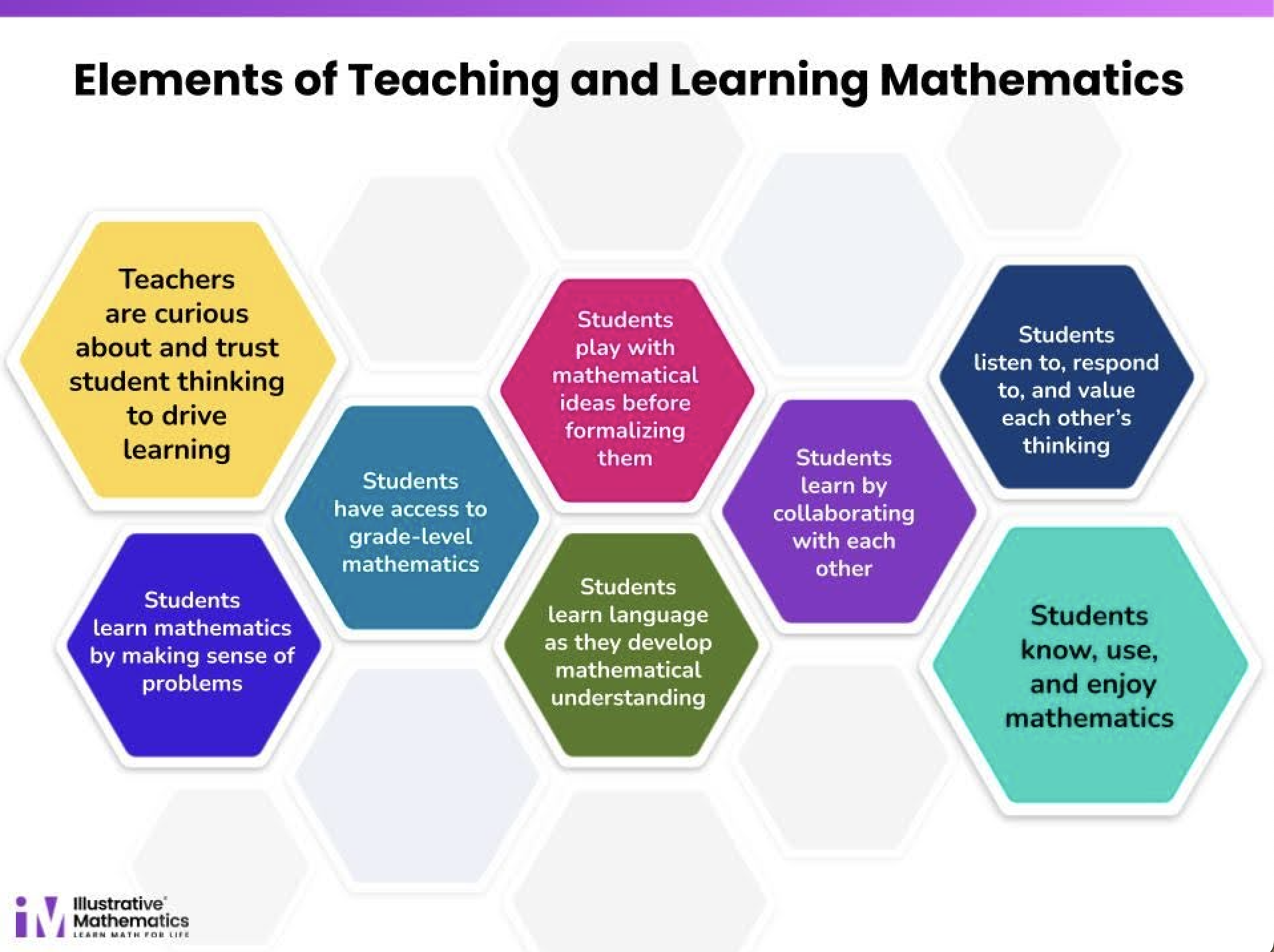
Here are some things that may have stood out for you:
- There are some gray hexagons without words on them.
- Some hexagons are bigger than others.
- Most of the hexagons are about students, but one is about teachers.
Several years ago, IM’s curriculum and professional learning teams came together to talk about what we wanted to highlight for teachers learning about our approach to problem-based instruction. We thought about classrooms that we’ve visited (some of yours!), and reflected on questions and concerns from professional learning participants (some of you!). In response to these concerns, we created these elements of problem-based teaching and learning that now serve as an anchor for our teams as we design learning experiences.
We purposely included the gray hexagons as a visual reminder that we haven’t created a conclusive list. What would you add? The larger hexagons are a premise and our hopes for a powerful outcome. For us, problem-based learning starts with curiosity and trust, specifically with teachers being curious about their students’ ideas and excited to see where their students’ thinking will lead. The other elements work in tandem to ensure students arrive at IM’s vision of a world where all students know, use, and enjoy mathematics.
How do these elements play out in your classroom? What do they look like and sound like? Here are some added details based on our observations during our classroom visits.
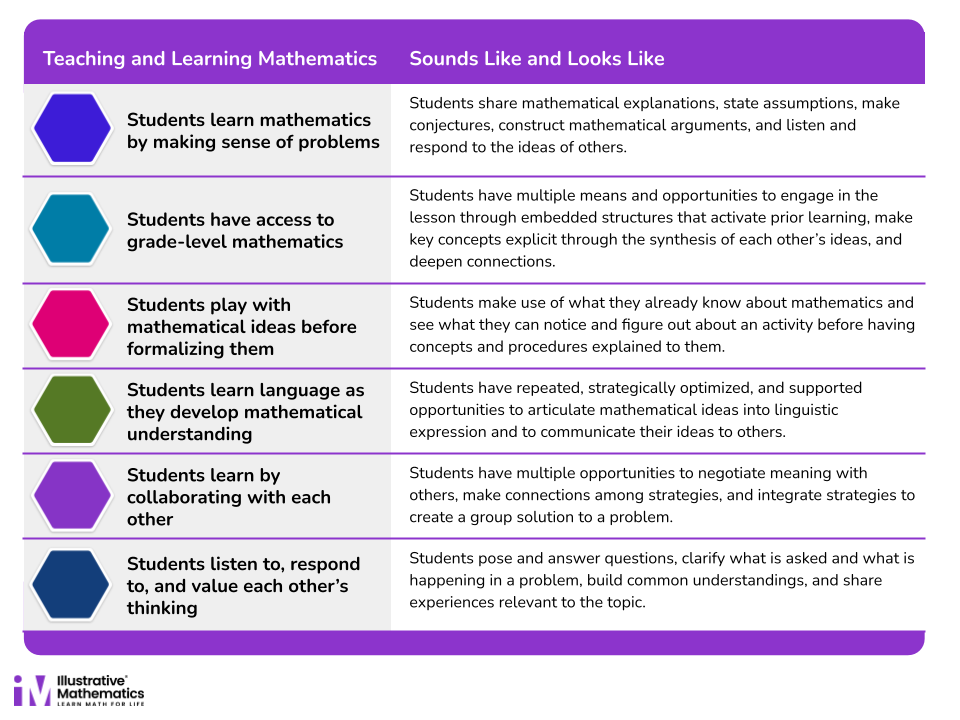
Each element of problem-based learning on this list contributes to an ultimate goal: to create the conditions for every student to experience a sense of belonging so they feel empowered to know, use, and enjoy mathematics in class and in their daily lives. And even better than a list of suggested look-fors, we have examples of what these elements look and sound like in a school district in Iowa.
(Click and drag in the VR video below to move the camera.)
To learn more about the work happening in Iowa, check out their case study.
Teachers and students in a New Mexico district got to reflect on the elements like you just did as they watched a live video feed of students participating in a MathLab summer program and noted the elements they saw.
Here are a few quotes from middle-grade teachers sharing what they learned:
“You need to . . . witness these good teaching practices, and really be thoughtful of how the elements of problem-based teaching and learning are purposely laid out. I am always reminded of how Vince Lombardi is quoted to say ‘Practice doesn’t make perfect. Perfect practice makes perfect.’ You need to witness and thoroughly think about what you as a teacher are going to do.”
“Let go of control. Trust your students and the curriculum to get the learning where you need to go. You don’t need to steer.”
Here’s what their students had to say as they reflected on their IM experience when the elements of problem-based teaching and learning were a focus:
“I thought it was really cool how safe of a space it was, how everyone was able to share their thoughts and the way they thought and their questions without being judged.”
“A really good way that makes it safe is being able to talk with friends and share ideas. That just helps me a lot. It can be distracting at times but it can also be very helpful.”
“I wanted to add on to what [the previous student] shared; working together as a team was very helpful.”
In these reflections we can see not only evidence of the elements of problem-based teaching and learning, but also how teachers’ and students’ beliefs about math and their roles in the classroom shifted. This connection between the elements and our beliefs about students and educators is important to us.
The elements of problem-based teaching and learning are grounded in IM’s beliefs about teachers and educators:


This is what we believe and hope for in IM Classrooms, but we know that isn’t enough. To thrive, teachers and students must also embrace these beliefs not only about themselves but also about others in their learning communities.
How have you seen these beliefs play out in your own classroom and school?
What connections do you see between these beliefs and elements on your journey to a world where all students know, use, and enjoy mathematics?
Whether you have encountered the “hexagons” before or this is your first time exploring them, we hope that you are making connections to your own practice. As you reflect on these elements, ask yourself what inspires you in the classroom and consider how your own beliefs about students and about educators influence the instructional decisions you make.
In The Future of Math Teacher Professional Learning, the authors state, “A teacher’s views of their student’s math capabilities is a predictor of their student’s math performance. A critical first step to real change for learners underestimated by the system is to engage teachers to critically examine their beliefs and assumptions.”
As mathematics teachers, we respond daily to the call to action to provide equitable instruction and to position all students in a way that supports learning. The most impactful IM Experience will be the one that you and your students cocreate as you believe in, value, and get curious about each other’s thinking.
As you plan for an upcoming lesson/math party, consider:
- We invite you and your students to take some time to reflect.
- How have you experienced the elements of problem-based teaching and learning?
- What element or belief will you highlight and focus on in the coming weeks?
 Max Ray-Riek
Max Ray-Riek
Senior Director, Teacher Professional Learning
Max Ray-Riek is the senior director of teacher professional learning at Illustrative Mathematics. Before joining IM, Max worked for The Math Forum. He is the lead author of Powerful Problem Solving: Activities for Sense Making with the Math Practices. Max is a former secondary mathematics teacher (and before that, preschool teacher) who finds the art and discipline of valuing each student’s ideas, and supporting all students to see themselves as “mathers,” to be hard, rewarding, and important work. Max and his partner Kaytee live in Delaware County, Pennsylvania, where they raise service dogs.
