By Ashli Black
The fact that a line has a well-defined slope—that the ratio between the rise and run for any two points on the line is always the same—depends on similar triangles.
(p.12, 6–8 Progression on Expressions and Equations)
As students are building their understanding of dilation at the beginning of grade 8 in Unit 2 of the LearnZillion Illustrative Mathematics 6–8 Math curriculum, an activity asks students to dilate different quadrilaterals using a given center and dilation factor on a square grid. Here are the results of two of the dilations in that activity involving triangles:

One of the things I really enjoy about the curriculum is the foreshadowing of the big ideas in a unit. In the case of Unit 2, these images show how students work with similar triangles in Lesson 4 in a way that will pay dividends in Lesson 10 where slope is introduced. In fact, the dilation of a right triangle along the line described by its hypotenuse links to one of my favorite standards in grade 8; specifically the first bit of the standard that says “Use similar triangles to explain why the slope m is the same between any two distinct points on a non-vertical line in the coordinate plane.”
Students use previous understandings such as determining and representing proportional relationships to establish similarity of figures. They have shown that the quotients of corresponding sides of similar polygons are equal, with special attention paid to triangles. Then, Lesson 10 in Unit 2 has students work out why any two slope triangles on a given line must be similar. We defined a slope triangle as “a triangle whose longest side lies on the line and whose other two sides are vertical and horizontal”. From there the idea of slope is established as a feature of a line calculated as the quotient of the length of the vertical side and the horizontal side of any slope triangle drawn for the line.
Establishing slope through similarity of triangles helps students build on their understanding of the slope of a line as they reason about other points on a line and even write equations for the line. In fact, the very next lesson after slope is established is titled “Writing Equations for Lines,” but you won’t find any $y=mx+b$ in this lesson.
Let’s look at an example. For lines like $j$ shown here that go through $(0,0)$, we can use the knowledge that all slope triangles for a line are similar triangles to write the equation $\frac{y}{x}=\frac{3}{4}$, which is true for all points $(x,y)$ on the line.
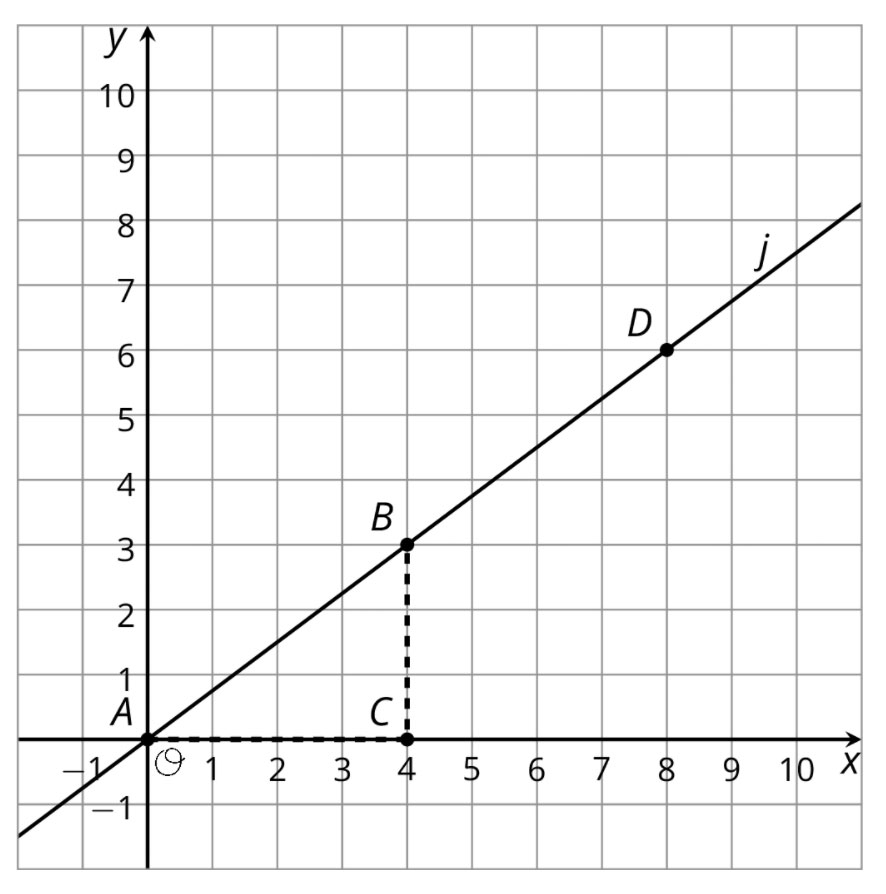
And what if we have a line $k$ not through the point $(0,0)$, like the one shown here?
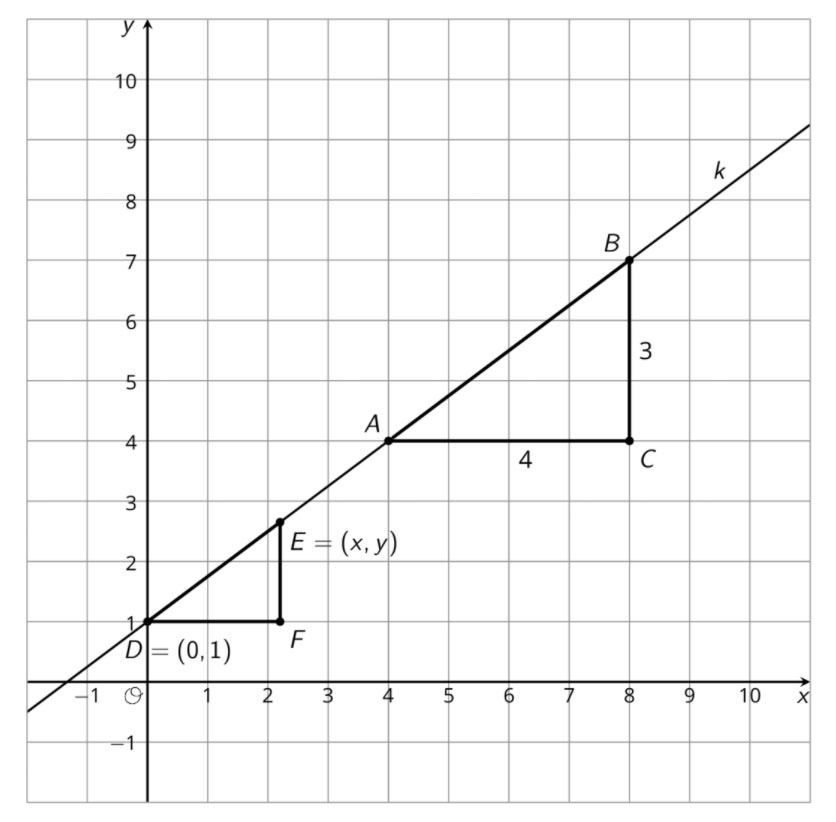
Well, line $k$ doesn’t represent a proportional relationship, but it still has a slope and any two slope triangles for line $k$ must have the same quotient between their vertical and horizontal sides. This means $\frac{y-1}{x}=\frac{3}{4}$ is an equation that is true for any point $(x,y)$ on line $k$.
How do equations in this form change the way students think about linear relationships? I would argue that while they look strange to someone raised under the bright light of $y=mx+b$ (like myself), they make a lot of sense to a student who has spent quite a bit of their time in math class thinking about, writing, and solving proportional relationships.
Next Steps
- What other paths to slope do you like? Let me know in the comments!
- Check out the 6–8 Progression on Expressions and Equations here.
- Check out the 6–7 Progression on Ratio and Proportional Relationships here.
- Read about how the last lesson of this unit was designed here.
- Read more about lines in the blog post Why is the graph of a line straight? here.
- Learn more about the LearnZillion Illustrative Mathematics 6-8 Math curriculum here.
Mathematical images shown in this post are excerpted from Open Up Resources Grade 6 – 8 Math by Open Up Resources used under CC BY 4.0. Download for free at www.openupresources.org.
