By William McCallum
You will never have to subtract again.
Students sometimes learn about addition and subtraction of integers using integer chips. These are circular chips, with a yellow chip representing +1 and a red chip representing -1. You start with the all-important rule that $1 + (\text-1) = 0$, so you can add or remove a red-yellow pair without changing the number. To calculate the right hand side of the equation in the title, $3 + (\text-5)$, you put 3 yellow chips together with 5 red chips, then remove 3 red-yellow pairs, leaving 2 red chips. So $3 + (\text-5) = -2$.
How do you calculate the left hand side, $3 – 5$? You want to take 5 yellow chips away from 3 yellow chips, which you obviously can’t do, so you add 2 more red-yellow pairs, then take away the 5 yellows, and you are again left with 2 reds, so $3 – 5 = \text-2$. So $3 – 5 = 3 + (\text-5)$.
I can see the value of integer chips in making calculations concrete, but I see some significant problems with them as well. One is that the step of removing or adding red-yellow pairs, although easy to do, is conceptually sophisticated and a little mysterious. Another problem is that integer chips don’t generalize well to working with rational numbers. Yet another is that although integer chips can be used to show that the equation in the title is true, they don’t leave a record of the calculations that enable you to reason about why it is true. Maybe it was a coincidence that it worked out with the numbers 3 and 5. There is a danger that “subtraction is addition of the opposite” could become a meaningless mantra. Finally, integer chips are problematic when you start thinking about contexts for negative numbers because in many contexts negative numbers represent the absence or removal of things, whereas red chips are clearly present things. See, for example, the discussion of contexts in Nik Doran’s blog post.
In order for students to see why the rules for operating with negative numbers are true, the IM 6–8 curriculum introduces negative numbers using number line diagrams. This makes sense because grade 6 students have been working with the number line for a few years and have moved on from discrete representations of addition and subtraction (which integer chips push them back to). In a number line diagram, negative numbers are just points to the left of zero. We don’t really care anymore if they are integers. To think about how to add and subtract them, let’s go back to adding and subtracting positive numbers. To represent $3 + 5 = 8$ I put line segments of lengths 3 and 5 on a number line diagram and end up at 8. (Notice that I have snuck some arrowheads onto the segments for reasons which become clear in a minute.)
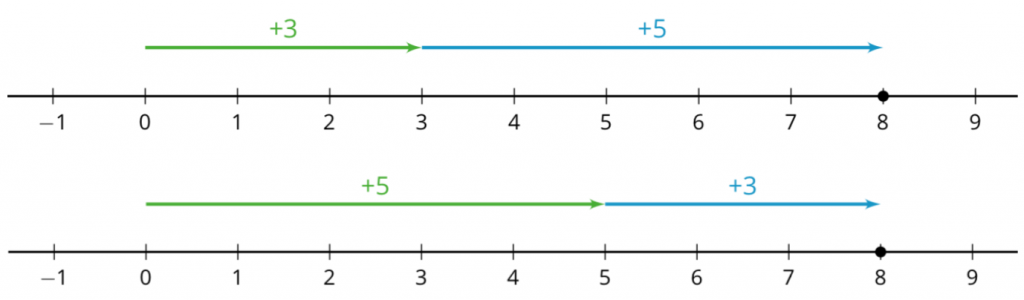
Note that this diagram can also be used to represent $8 – 3 = 5$ because $8 – 3$ is the unknown addend in $3 + ? = 8$, that is, $8 – 3$ is the number you add to 3 to get 8. The diagram shows me that that unknown addend is 5. In fact every subtraction problem can be represented by an addition diagram. I’ll reveal the awesome power of this observation in a moment, but first, how do we represent addition of negative numbers? This is where the arrows come into play. Positive numbers are represented by arrows pointing to the right, negative numbers by arrows pointing to the left. So $3 + (\text-5)$ is represented the same way as $3 + 5$, except the arrow for -5 goes to the left, ending up at -2.
Addition diagrams always work the same way. You put an arrow from 0 for the first addend, then you put an arrow for the second addend starting at the tip of the first arrow, then figure out where you have landed on the number line.
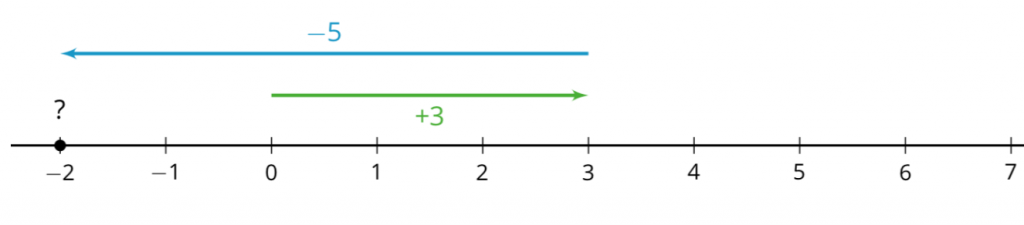
What about subtraction? Remember (drum roll) that every subtraction problem can be represented with an addition diagram. Let’s try this out for $3 – 5$. The addition equation corresponding to $3 – 5 = ?$ is $5 + ? = 3$ (“3 – 5 is the number you add to 5 to get 3”). The addition diagram for this would start with an arrow to the right for 5, and would land on 3. What is the arrow that gets from the tip of the arrow for 5 to the point at 3? It is the arrow for -2.

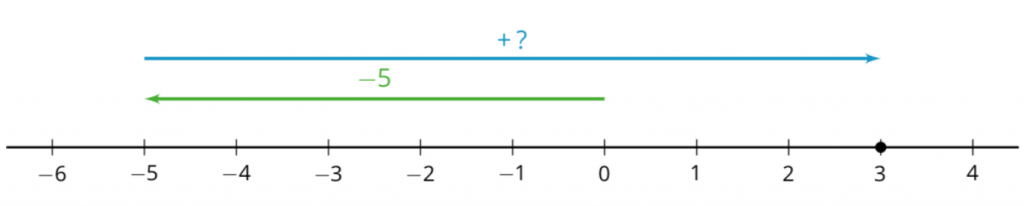
Okay, that one was easy. What about the bête noire of all students, subtracting a negative number? Let’s try $3 – (\text-5)$. The addition equation corresponding to $3 – (\text-5) = ?$ is $(\text-5) + ? = 3$. In this case the missing arrow goes all the way from -5 to 3, so it is the arrow for 8.
I understand why a teacher might prefer integer chips to addition diagrams. Once you have learned the rules they are pretty simple. Addition diagrams may be more difficult initially because you have to think about how to express the subtraction problem as a missing addend problem when using them. But that thinking pays off later in a more durable understanding of operations with rational numbers (“$a-b$ is the arrow I add to $b$ to get $a$”). Integer chips are a way of doing; number line diagrams are a way of thinking.
Next Step
Question: How can you use addition diagrams to show why $3 + (\text-5) = 3 – 5$?