By Greta Anderson & Patti Drawdy, IM Certified Facilitator
I read the lesson three times through, but was still unsure why the number line below shows $3 – 7$. My aha moment arrived courtesy of the grade 1 standards.

Greta: Over the course of this past year, fellow IM Certified Facilitator Patti Drawdy and I have facilitated many unit overviews together. We make quite the team: my background is in elementary and middle school content, whereas Patti works primarily with middle and high school. Between the two of us, we usually figure out mathematical progressions: where standards build from, and where they are going toward.
This fall, we were forewarned that an upcoming concept—subtraction of signed numbers using number lines—might be particularly challenging. I was skeptical. Though I was an algebra tiles devotee, I certainly used and appreciated number lines, and wondered why anyone would find subtracting signed numbers with number lines hard. $3 – 7$ means starts at 0, move 3 right, then 7 left. End at -4. Therefore, $3 – 7 = \text- 4$. Done and done.
Or so I thought. As I read through the featured lesson in the unit launch, I looked at $3 – 7$ and searched for the number line I described above, but instead found what seemed like an incomplete number line. I read the lesson three times through, grappling with why the number line below shows $3 – 7$. My aha moment arrived courtesy of the grade 1 standards.

It just clicked for me: this is counting on to find the difference. It is the same math that allows a student to think of $19 – 17$ as starting at 17 and adding up 2 to get to 19 instead of taking away 17 from 19 or writing out the algorithm.
$19 – 17 = \underline{\hspace{0.5in}}$
$17 + \underline{\hspace{0.5in}} = 19$
This approach allows students to see that subtraction is finding the difference between two numbers, which offers a more robust understanding of subtraction than simply taking away. Since students eventually move away from counting, a more appropriate term for this approach would be rewriting an equation in which two numbers are subtracted as a missing addend equation. A student seeing $3 – 7$ might think, “If I start at 7, how many spaces would I move left or right to end at 3?” in the same way a student seeing $100 – 92$ might think, “If I start at 92, how many spaces would I move left or right to end at 100?”
$3 – 7 = \underline{\hspace{0.5in}}$
$7 + \underline{\hspace{0.5in}} = 3$
This interpretation of subtraction is so embedded in our adult minds that we often don’t realize that we’re using it. When I owe \$8.25 and pay \$10.00, I often rework this subtraction to be an addition sentence with a missing addend without even realizing I’m doing it:
$\$10.00 – \$8.25 = \underline{\hspace{0.5in}}$
$\$8.25 + \underline{\hspace{0.5in}} = \$10.00$

This approach saves me pencil, paper, and the toil of “regrouping across zeros” using the standard algorithm. If you don’t use a pencil and paper or calculator to figure out how many more steps you need to take to reach a 10,000 step daily goal, you are probably using this technique!
With this in mind, it makes sense that we could use the same approach with signed numbers:
$\frac12 – \frac34 = \underline{\hspace{0.5in}}$
$\frac34 + \underline{\hspace{0.5in}} = \frac12$
$\frac34 + (\text-\frac14) = \frac12$
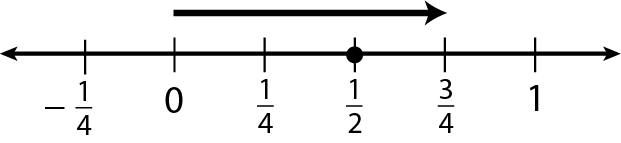
The number line approach to adding and subtracting signed numbers also helped me understand one of the limitations of algebra tiles. The number line pushes our understanding of both types of subtraction and transfers seamlessly to non-integers, whereas the algebra tiles only served to help me compute sums or differences of integers within a limited range.
With this more complete understanding, I was able to offer some perspective as to why this representation is a natural extension of elementary school representations. Patti was the one to help me see the clear bridge to secondary mathematics and science.
Patti: Co-facilitating with Greta has helped me tap into my roots as an elementary teacher and consultant, since my most recent work has been with grades 6–12 mathematics. With IM, I’ve learned to think like students and consider what content they might be bringing up that I can amplify rather than pushing down high school/college mathematics content knowledge. Greta’s connection to grade 1 was insightful. I totally embrace number lines as a visual representation for mathematics across the grades. Yet, I must admit in prepping for these lessons, I wondered “Where are the two-color counters?”
Then, I read William McCallum’s blog post and was intrigued by the final line: “Integer chips are a way of doing; number line diagrams are a way of thinking.” Greta’s aha reminded me that students in elementary school have developed ways to think about operations using number lines that we can build on as we introduce negative values. I now see that a chip model emphasizes subtraction as take away, not as the difference between two numbers, and using manipulatives that represent discrete quantities won’t work for all rational numbers.
Using number lines for addition of signed numbers made perfect sense for me and for teacher and student groups with whom I’ve worked. Still, most of us grapple a bit with the number line representations for subtraction of signed numbers. While I’ve learned to celebrate that “grappling” process in my own learning, in facilitating the learning of others, there is a temptation at times to shortcut the process and revert to teaching procedurally. Instead, I’ve learned to invite and leverage curiosity. I support thinking through questioning and listening. We talk about and make sense of the content together.
Now, let’s think about enactment. When facilitating a task to match number lines with addition or subtraction expressions, I anticipated productive struggle, and wanted to guard against a temptation to teach procedurally. So, I launched the task by first focusing on just the number lines with an inquiry stance: Let’s be curious and look for patterns and structure in the diagrams. What do you notice? What do you wonder?

(From student materials in IM MS Unit 7.5 Lesson 5 Activity 3. Note: Teacher materials requires free registration.)
I found that most learners notice some representations have two arrows without a point marked by a dot on the number line, while others have only one arrow with a point on the number line.
My next prompt was: “Let’s sort the number lines into two groups: the ones we think are combining values to find a sum, and the ones we think show finding differences.”
After a brief discussion, then there was work time for problem #1: match each representation with the given expressions: $3 + 7, 3 – 7, 3 +(\text-7), 3 – (\text-7)$. After more work time and synthesis, the learners were ready to move on to problem #2, above. A next step in facilitating the task was a prompt to group the expressions with the same value and ask: “What do you notice?” A common response is how the number line representations look really different, but the expressions $3 + 7$ and $3 – (\text-7)$ have the same value, and so do $3 +(\text-7)$ and $3 – 7$. Noticing this pattern and the structure of the expressions leads to wondering if this will always work with subtraction and “adding the opposite,” which is where we want a lesson introducing subtraction of signed numbers to land. Yes, we can reimagine a difference as a missing addend and flexibly rewrite subtraction equations as addition equations.
Why did the IM authors choose this representation that seemed so perplexing at first? As Greta and I reached out for clarification, Kate Nowak, IM’s Director of 6–12 Curriculum, offered these insights:
“We wanted to be consistent with the way students would see the coordinate plane and vectors in later courses. A positive value is represented either by an arrow pointing right or a location to the right of 0. A negative value is represented either by an arrow pointing left or a location to the left of 0. Note that this means that subtracting a positive number should not be represented by an arrow pointing left. When two values being added are represented by arrows, the arrows get placed head to tail.”
This approach has expanded my thinking about the many nuances of addition and subtraction. Seeing subtraction as a difference is really important for future work! For example, understanding the meaning of most formulas derived in the study of analytic geometry, like the slope formula and the distance formula, depends on this foundational understanding. Representing distance or directed distance on number lines prepares students for advanced mathematics and science. Vector addition is a key feature of introductory physics and statics courses. This representation works across the entire K–12 continuum of learning.
Next Steps
What is exciting is how the IM curriculum brings the standards to life in a way that invites all learners to be curious and think deeply, including students, their teachers, and facilitators! Each new challenge or question, such as this one, is an opportunity to develop a more robust understanding of the grades K–12 mathematics progressions. As our understanding as educators deepens, so does our flexibility and craftsmanship in facilitating a problem-based approach that develops learners’ identity and agency as math thinkers. Let’s give a shoutout to all teachers who are in their first year(s) of teaching with IM 6–8 curriculum! What challenges have you grappled with that have deepened your understanding and increased your flexibility in facilitating mathematics learning?
