By Kristin Gray, Director of K–5 Curriculum & Professional Learning
One challenge in curriculum design is considering all we know and believe to be true about math teaching and learning and translating that into realistic and actionable pieces for teachers and students. Our recent post about the K–5 curriculum focused around our belief that each and every student should be seen as a unique person with unique knowledge and needs. And while that post centered on elementary materials, to truly design around this belief we must look past K–5 to consider each student’s unique K–12 mathematical journey. A journey that, for most students, looks very different as they move from elementary to middle to high school.
While it is not surprising that the math content is different across grades, there is something really important and powerful in curriculum design that can make a student’s mathematical journey much more connected and accessible than it currently is. As we write the final component of our complete K–12 OER math curriculum, we continually focus on the consistent structures that support the focused, coherent mathematics within, and across, grade levels.
Why consistent structures for students?
Consistent problem-based curriculum structures can help remove some of the guesswork and anxiety about how math class is going to look and feel each year. Imagine a student entering any grade level knowing they will be given the opportunity to grapple with mathematical ideas, both independently and with their peers, before being expected to apply the understandings on their own. The problem-based atmosphere supports students in understanding their important role as a mathematical thinker and over time students get used to generating the mathematical knowledge as a community of learners.
Within our problem-based design is a consistent lesson structure:
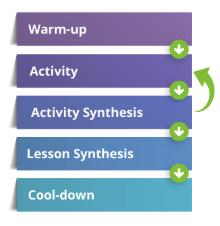
This means every day, no matter what grade they are in, students know they have an accessible invitation to the mathematics during the warm-up, are given opportunities to build ways of thinking and doing the mathematics, discuss the ideas of the lesson as a whole group during the synthesis, and show what they know on the cool-down. This predictable flow allows students to focus on the math of the lesson because they know there will be opportunities to discuss ideas, ask questions, and consolidate their learning.
Another important consistent structure within the curriculum are the instructional routines. Instructional routines provide an opportunity for all students to engage in, and contribute to, mathematical conversations. The predictable routine for the interactions between teachers and students allows each student in the classroom to focus on the mathematics rather than the actions that need to be taken. And the more experience students have with the routine gives them greater ability to focus on the mathematical content.
Why consistent structures for teachers?
Within the classroom, consistent structures give teachers time to focus on what’s most important—the students. As a teacher, there is something really nice about not having to worry about “what comes next” in a lesson or “how the activity runs,” just as it is for students. When all of those things are kept consistent, it offers teachers the time to listen for the mathematical understandings students have and think more deeply about the classroom experience: What questions are being asked? How are they are asked? With a consistent structure, there are more opportunities to think about whose ideas are being shared, and the ways in which these ideas are represented.
Outside of the classrooms, it would be amazing to have the opportunity to collaborate K–12 in professional learning. I would love to have a world where a district did not always split into K–5, 6–8, and 9–12 math professional development sessions, but instead had a room of K–12 teachers discussing the coherent progression of mathematical ideas, representations, or routines in a curriculum.
For example
Below is a series of warm-up routines from the IM math curriculum by grade. While there are some really cool math connections that show up in this series, I would like you to imagine a student who experienced the structure of these routines since kindergarten.
- What might they know about the structure of the routine by the time they are in Algebra 1?
- How might what they know about the structure help them attend to the mathematics more by the time they reach Algebra 1?
- How might what they know about the structure help them be seen as a unique person with unique knowledge by the time they reach Algebra 1?
Kindergarten
Warm-up from Kindergarten, Unit 5, Lesson 8
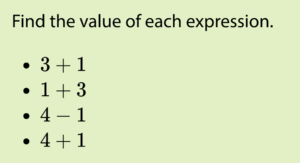
Grade 2
Warm-up from Grade 2, Unit 2, Lesson 4
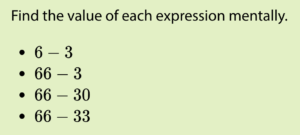
Grade 3
Warm-up from Grade 3, Unit 8, Lesson 8
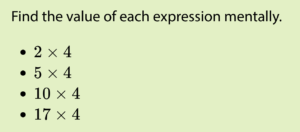
Grade 6
Warm-up from this lesson (labeled 8.1)

Algebra 1
Warm-up from this lesson (labeled 13.1)

Next Steps
We would love to read your reflections to the questions above! Please respond in the comments.
