By Noelle Conforti Preszler and Kristin Gray
In the following activity, think about the students in your classroom. How might each respond?
What do you notice? What do you wonder?
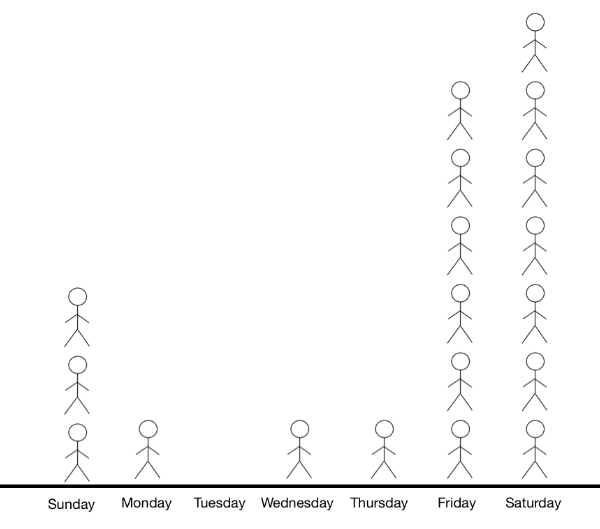
This activity is the drafted warm-up of the first lesson in Grade 3, Unit 1: Introducing Multiplication. While we believe the structure of this activity — “What do you notice? What do you wonder?” — implicitly supports equity, it is the word each in the question at the top that has become central to our design of the IM K-5 Math curriculum.
Discussions within and beyond the K-5 writing team focus on the impact of each unit, lesson, and activity on each teacher and each student. At the same time, we also recognize the possibilities, and limitations of, curriculum materials. These discussions influence our decisions on the overarching curriculum design and, in turn, the principles that guide our choices about student tasks, teacher prompts, and lesson plan structure. While it would be easy to simply say ‘we considered equity in our design,’ people define and interpret the word “equity” in different ways. As we continue to learn and refine our design principles, we want to share what equity in mathematics learning and teaching means to us, and give you a sense of how it explicitly impacts the materials we are creating for the K-5 curriculum.
In our classrooms, each and every student should be seen as a unique person with unique knowledge and needs.
Equity at the Center of Design
All students come to the mathematics learning community as capable learners and doers of meaningful mathematics, each with unique knowledge and needs. Mathematics instruction grounded in equity must provide students access to grade-level content, with appropriate scaffolds, and provide teachers with necessary guidance. Materials that support this instruction must leverage and enhance the teacher’s knowledge of mathematics, their students, and the socio-cultural contexts of each student in the classroom. This is no small task. We are committed to creating materials that help teachers understand their responsibility in positioning each student so their uniqueness is seen and valued. These materials will encourage teachers to reflect on, and challenge, the assumptions they make — about mathematics, learners of mathematics, and the communication of mathematics in their classrooms.
So what does this look like in the materials? To discuss all of the implications would be impossible in one blog post, so let’s narrow our focus and revisit the Notice and Wonder activity through this lens.
Implications for Student Learning
This particular prompt invites students to draw on what they know about not only the mathematical content of data representations from Grade 2, but also their own experiences. They may ask questions about the math such as ‘What does this graph represent?’ or ‘How many more stick people are on Friday and Saturday than the other days?’ but also prompts questions such as “What do I do more often on Friday and Saturday than other days of the week?” “I wonder where my stick person would go on that graph?” “What do people I know never do on Tuesday?”
In the remainder of this lesson, students ask and answer questions about information in a picture graph and compare picture graphs to bar graphs. Through accessible contexts, students have the opportunity to share things about themselves with one another. In upcoming lessons, they’ll be introduced to multiplication as they reason about scaled graphs in which each picture represents more than one. When we pose grade-level mathematical tasks with accessible entry points, and give students the space to share their ideas, students have the opportunity to see themselves as mathematical thinkers with worthwhile ideas and perspectives.
Implications for Teaching
The teacher has many roles in every activity: listener, facilitator, questioner, and more. In all of these roles, teachers must leverage student thinking, be mindful about who participates, and continuously be aware of how students are positioned in terms of status during the work. To help teachers in these roles, we provide a number of supports within each lesson plan. We include the mathematical purpose of each activity, as well as how the activity is situated in the lesson. Lesson plans also include potential student responses and questions to help facilitate the discussion and synthesize the learning. These supports are all designed to help teachers continue to develop as listeners, facilitators, etc.
The more difficult question is: how do we address teacher beliefs and understandings of both the mathematics and their students?
In the IM K-5 Math curriculum, the lesson plans explicitly invite teachers to reflect on these exact things. At the end of each lesson we pose a Teacher Reflection Question, and encourage teachers to keep a journal with their responses during the school year. We are still in the process of defining the types of questions, but we imagine these questions falling into buckets that we believe address equity in the classroom: Content Understanding, Pedagogy, Student Thinking, and Beliefs and Positioning.
Looking back at the opening activity, we could ask teachers to reflect on a range of questions. Since this is the first lesson of the first unit in grade 3, it would make sense to ask the teacher to consider how students’ grade 2 work around using information in a picture or bar graph came into play during the lesson. Reflecting on this may deepen a teacher’s understanding of and beliefs about this mathematical content.
Considering this lesson through the lens of seeing each and every student, we might also ask:
- Who participated in math class today?
- What assumptions are you making about those who did not participate?
- How can you leverage each of your students’ ideas to support them in being seen and heard in tomorrow’s math class?
Next Steps
We will be asking teachers to try these reflection questions during our alpha pilot in the fall, but in the meantime, we would love for you to try asking yourselves these questions at the end of a lesson and jotting your responses in a personal journal. What are your responses to each of those questions? How do your responses impact the next day’s lesson for each of your students?
As this IM K-5 Math blog series continues, we look forward to sharing ways in which our design principles impacted decisions on the organization of mathematical content, routines, representations, and lesson structures for teachers and students.
You can learn more about the K-5 Writing Team and curriculum design on illustrativemathematics.org.
