By William McCallum
When I started this series of blog posts on what it means to know, use, and enjoy mathematics, I thought this one would be the easiest. Math is fun, right? How could you not enjoy mathematics? I certainly do—I love the complexity in underlying simplicity, the pleasure of seeing a pattern and then finding an explanation for it, the intense joy when you have been working on a problem for a long time and finally solve it. But so what? Our vision at IM is not a world where mathematicians know, use, and enjoy mathematics. We want to reach all learners. And many learners have had their capacity for enjoying mathematics damaged by their experiences of school mathematics. So I thought it would be interesting to take a piece of school mathematics that is as ubiquitous as it is awful—PEMDAS—and see what pleasure there is to be obtained from it.
In my first post in this series, on what it means to know mathematics, I identified three levels: doing the math, seeing patterns, and interpreting and expressing mathematics. From the point of view of knowledge these form a hierarchy, each more sophisticated than the last. But from the point of view of enjoyment, they are all on the same level. It’s a bit like enjoying food or wine: some people enjoy it without thinking too much about it, others really get into it. Enjoyment is good at whatever level. So it is with mathematics. So let’s start with doing the math.
A good place to look for people enjoying things (and not) is Twitter. Every now and then a viral math problem erupts on Twitter. Someone asks “What is 6/2(1+2)?” and people get into arguments about whether the answer is 1, as in

or 9, as in
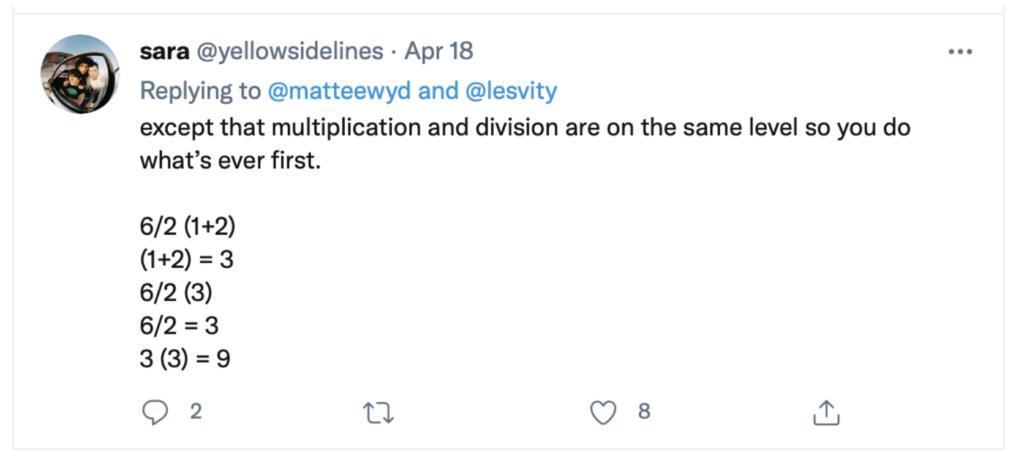
These people are enjoying mathematics! They learned how to do the math, in this case PEMDAS, in school, and they are enjoying using that knowledge. Of course the disagreement results from the fact that PEMDAS is a flawed way of talking about order of operations (see my blog post about order of operations here). But these people had fun arguing about it.
Moving on to the next level of knowledge, seeing patterns, there is a pattern to be found in these viral math problems.

What is the pattern? The use of the division symbol and the indication of multiplication by concatenation are from two different stages of a student’s journey, elementary school and middle school. It is this mixing up of notation that is the key to making these problems work. PEMDAS doesn’t make sense in middle school, once you start writing algebraic expressions. If you replace the numbers inside the parentheses with letters, you get:
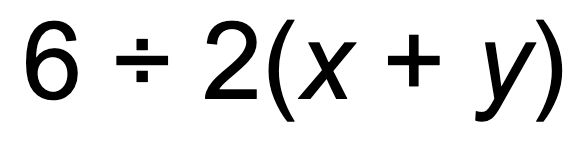
You can’t “do the parentheses” first in this expression. There is nothing to do in there. Furthermore, in middle school you’d be more likely to use a backslash instead of a division symbol, as in:
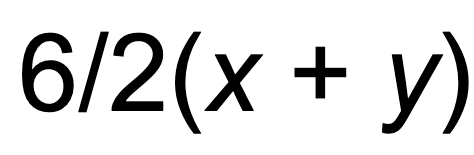
This pushes you further in the direction of the interpretation of the original expression as 3(1+2) = 9. The people who make up these problems are having fun with the pattern, exploiting the tension between the two systems of notation.
Finally, at the level of interpreting and expressing mathematics, we have this tweet:
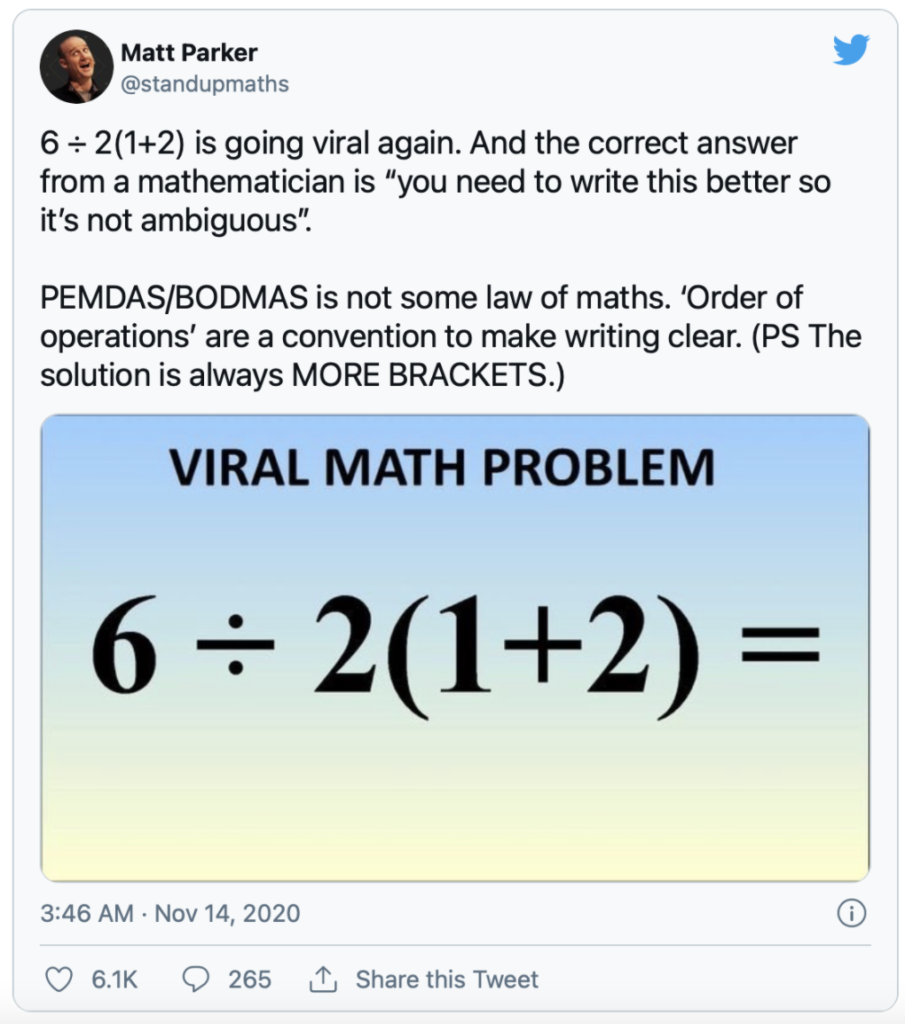
Following the suggestion of @standupmaths to use more brackets, we see that the two answers, 1 and 9, come from different ways of clarifying the expression:

That feeling of finally getting what is going on with this problem is one of the great pleasures of mathematics.
In the grand scheme of things, this viral math problem is not of great consequence. All the more does it illustrate that, even in its most inconsequential aspects, there is enjoyment to be had in mathematics, at all three levels of knowledge.
