“Some students are never given the opportunity to engage with mathematics in rich and meaningful ways that emphasize critical thinking and problem solving. Moreover, educators often use mathematics assessments to make definitive judgments about students’ competencies and abilities. Such judgments can follow students throughout their academic careers and have a long-lasting impact on how they see themselves as doers of mathematics (Boaler 2002, 2008; Jackson 2009; Martin 2000, 2009; Spielhagen 2011).”
As a problem-based curriculum, IM K–5 Math™ aims to offer all students opportunities to problem-solve and think critically about new learning. By design, students are expected to approach each lesson using the mathematical knowledge and cultural experiences they already have to solve problems. The guidance given in the teacher-facing materials support teachers with using this student knowledge as a launching pad for new learning. This basic design holds true for each mathematical concept in the curriculum, even in the development of procedural skills and fluency.
Often labeled asset-based or student-centered, this problem-based approach can have a lasting and positive impact on students’ mathematical identities. In this post we will highlight how procedural fluency with multiplication and division algorithms are developed within and across grades 3–5 in IM K-5 Math™. Along the way we will describe ways in which the lessons intend to position students as doers of mathematics and support the development of positive mathematical identities.
Fluency with Multiplication and Division Algorithms
As students shift from multiplying and dividing single-digit to multi-digit numbers, they begin to see the need for increased accuracy, flexibility, and efficiency with operations. Unfortunately, students who demonstrate limited knowledge of basic facts are often prevented from engaging in more complex tasks. The practice of using mathematical gatekeepers such as basic facts assessments to limit student access to grade-level content disproportionately affects Black and Brown students and can adversely affect students’ mathematical identities. (NCSM, TODOS 2016)
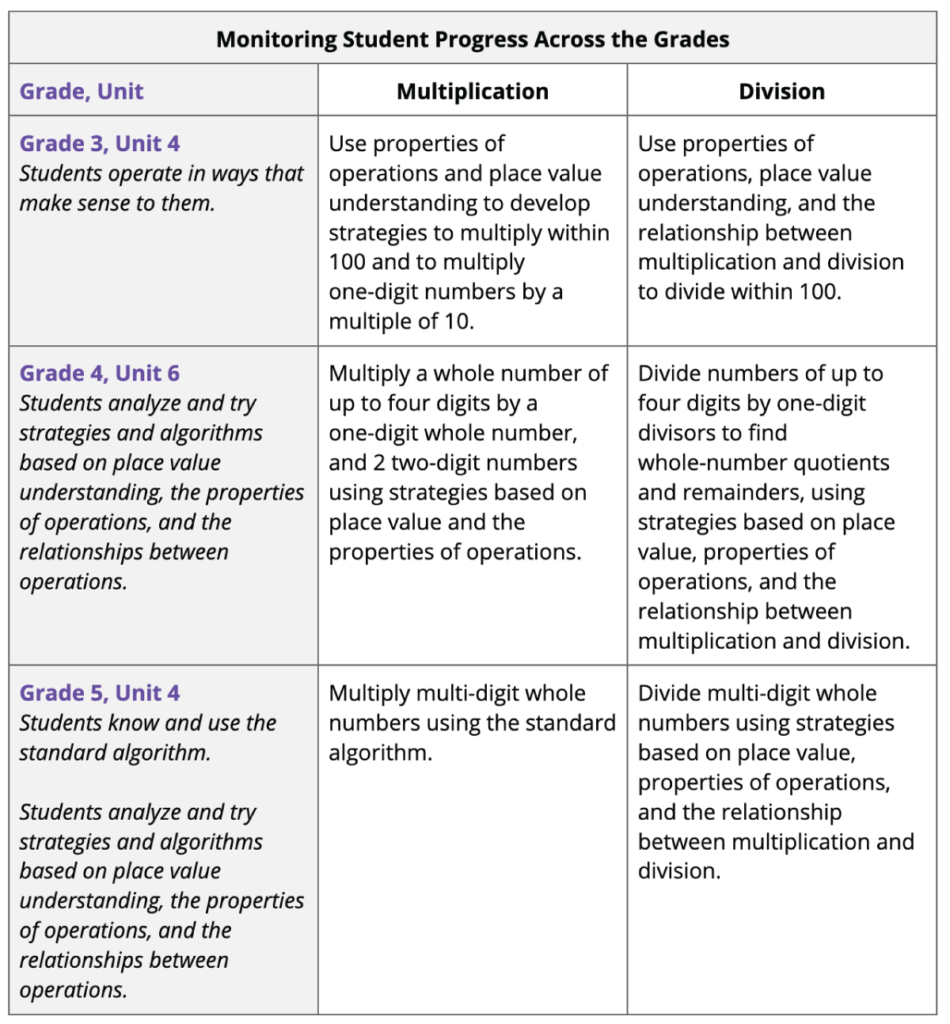
The IM K–5 Math™ curriculum intends to mitigate this practice through a coherent progression of units and lessons within and across the grades that allows students to develop procedural skills and conceptual understanding simultaneously. The Common Core Standards offer students two years of deep study to fluently use the standard algorithms for multiplication and division. The table below highlights the progression of learning from grade 3 to grade 6. Students start using the properties of operations and place value understanding to multiply in grade 3, which supports students to develop fluency with the standard algorithm for multiplication by the end of grade 5.
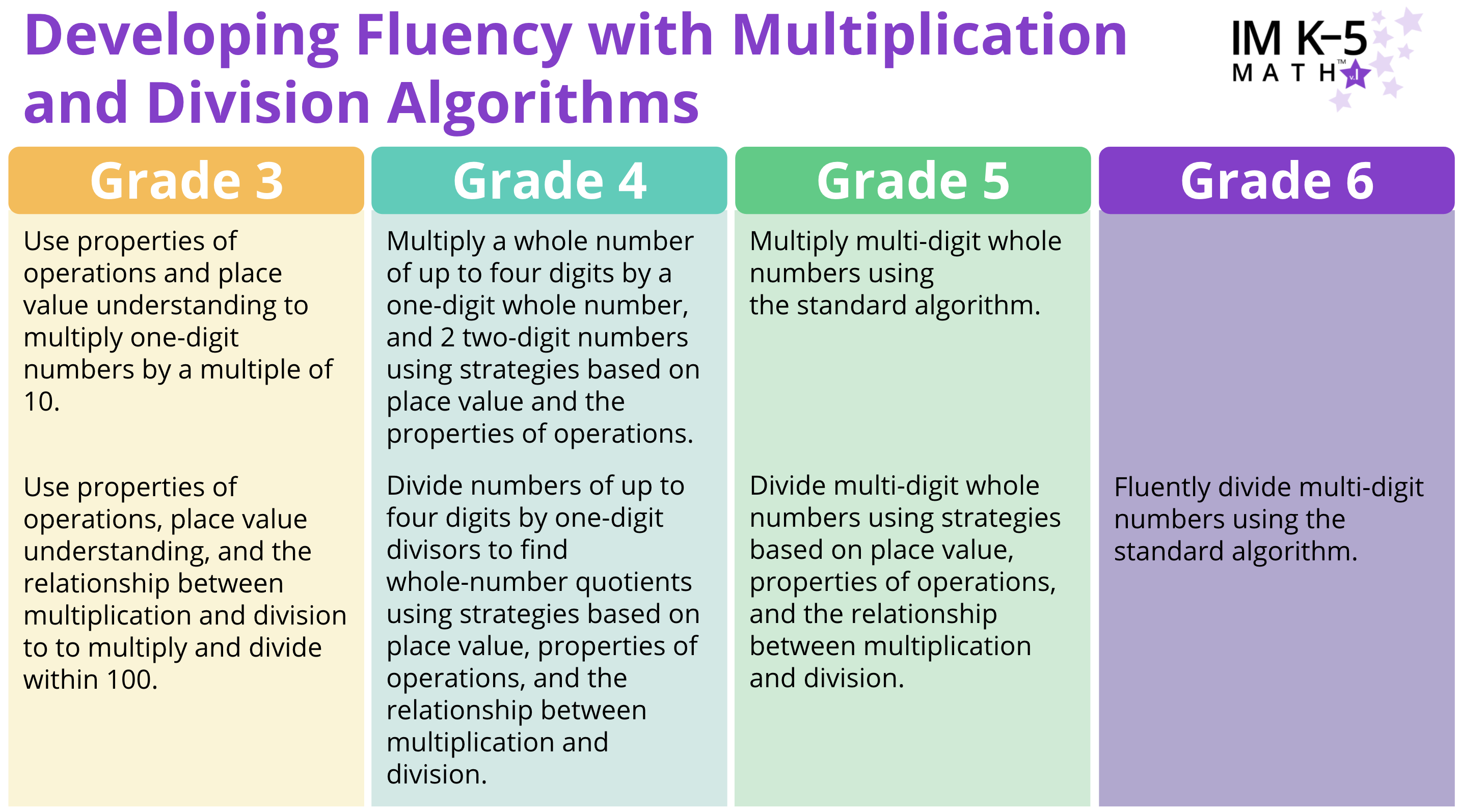
Fluency with the division standard algorithm is not expected until the end of grade 6, but students begin to use place value representations, the properties of operations, and their understanding of the relationship between multiplication and division to divide a multi-digit whole number by a single-digit number in grade 4.
In IM K–5 Math™, the process for developing fluency with an algorithm is the same for the four operations. In part 2 of this blog post series, we outlined the following steps:
- Students operate in ways that make sense to them.
- Students analyze and try strategies and algorithms based on place value understanding, the properties of operations, and the relationships between operations.
- Students know and use the standard algorithm.
These steps help to foster a positive mathematical identity because we start with what students know. We then center their ideas as they analyze new strategies, and give them space to make sense of algorithms before expecting fluency.
1. Students operate in ways that make sense to them.
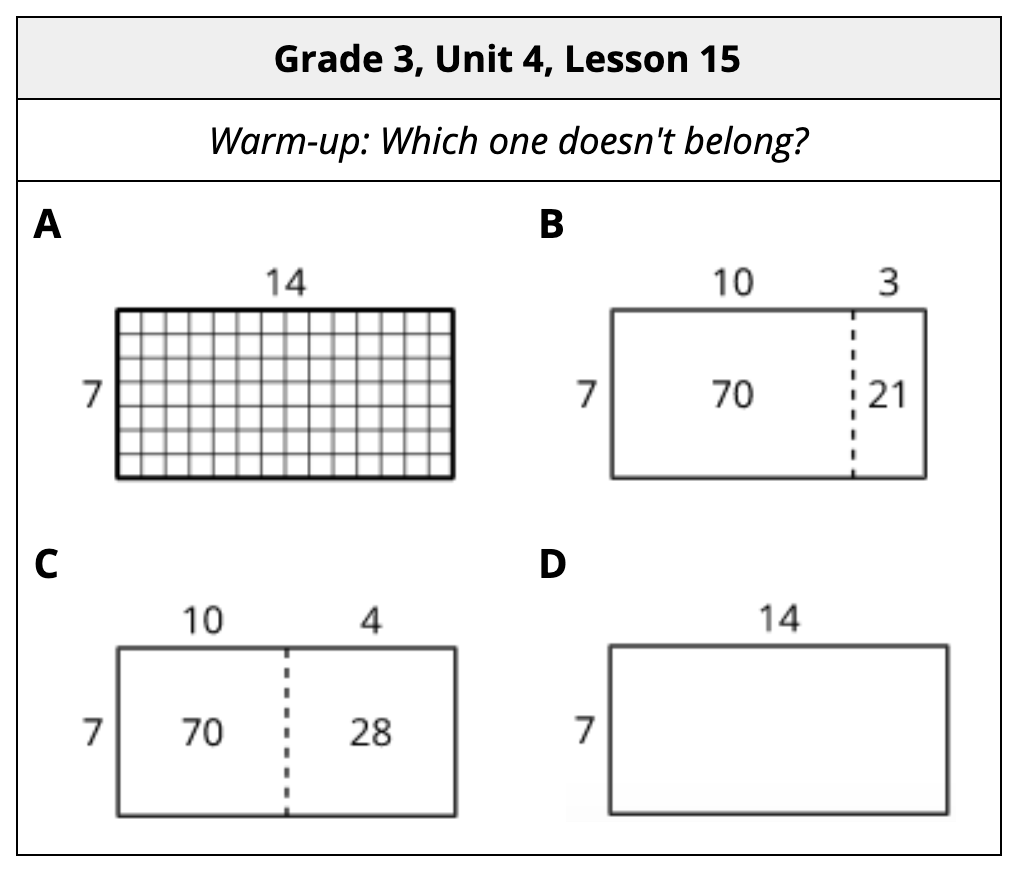
Students begin to multiply multi-digit numbers in grade 3. In Unit 4 of our Grade 3 course, students see that rectangles can help them reason about and use strategies based on place value understanding and the distributive property to multiply. In an earlier unit they learned that the side lengths of a rectangle can represent the two factors and its area can represent the product.
This warm-up in Lesson 15 helps students recall these concepts and begin to articulate how place value is used to decompose factors when multiplying larger numbers.
As students come to know these concepts, they gain flexibility in using them to approach more complex problems. In the example below, grade 4 students in a class in Portland, ME use place value reasoning and the properties of operations to find the value of 27 x 8. They use the strategy that makes the most sense to them.

Each student arrived at the answer accurately and efficiently, using strategies that decompose 27 into 20 and 7 to find the product. As students share their strategies and reasoning, they can make connections between strategies, build flexibility, and solidify their conceptual understanding.
2. Students analyze and try strategies and algorithms based on place value understanding, the properties of operations, and the relationships between operations.
Beginning in Grade 4 of our curriculum, students learn an algorithm that records partial products vertically. As they analyze this new written method, they connect it to how they recorded partial products in rectangular diagrams. In Unit 6, Lesson 9 students try this new method only after deep analysis and discussion.

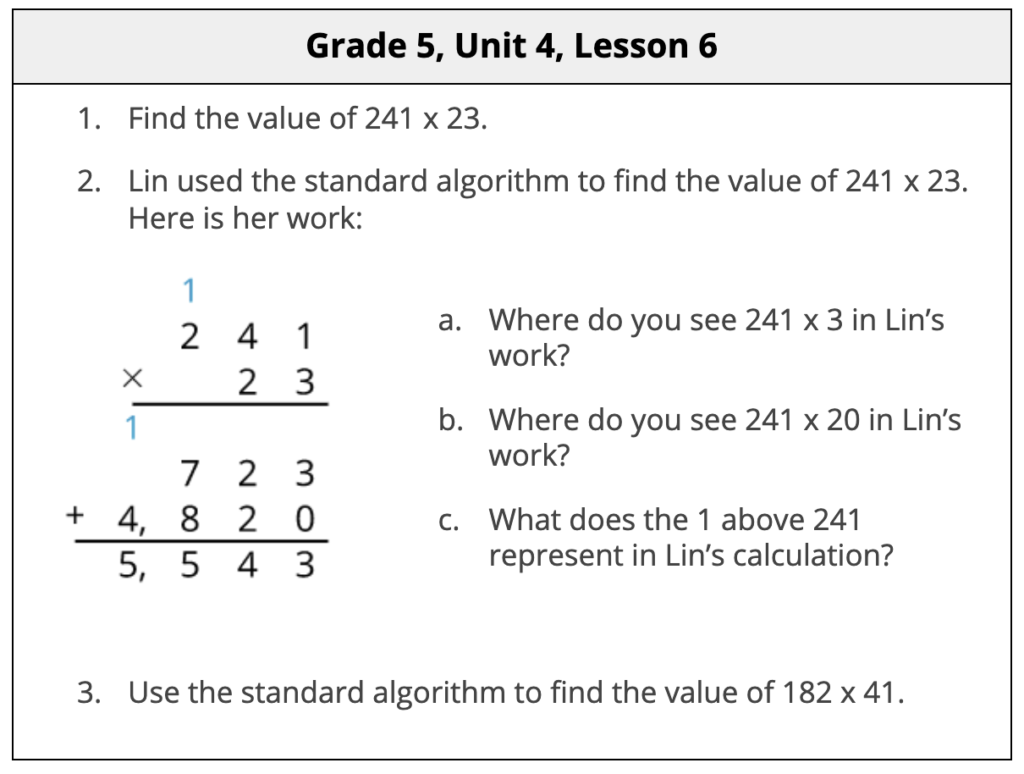
In Unit 4 of our Grade 5 course, students engage in a similar process to make sense of the standard algorithm for multiplication. They recognize that they can use place value understanding to record partial products in a more condensed way.
In Lesson 6 students are given time to analyze, make connections, and build conceptual understanding of the standard algorithm before being asked to use it to find the value of the product.
As stated earlier, offering students space to use what they already know to learn new concepts is key to developing positive mathematical identities, and is a foundational part of the design of our problem-based curriculum. We see this play out in our approach to developing students’ procedural fluency with division algorithms.
Beginning in Grade 4, students solve division problems in various situations, including those about equal-size groups, factors and multiples, and area of rectangles. These experiences reinforce students’ understanding of the relationship between multiplication and division.
The example below opens the section on division in our Grade 5 course. Here, a student in a class in Portland, ME uses what they know about partial products to solve a division problem.

To begin the work towards procedural fluency with the standard algorithm for division by the end of grade 6, our Grade 4 and 5 courses allow students to continue using what they know about place value, the properties of operations, and the relationships between operations to divide multi-digit numbers. They learn to use a vertical recording method to organize partial quotients by first analyzing and discussing the new method, then trying it for themselves.
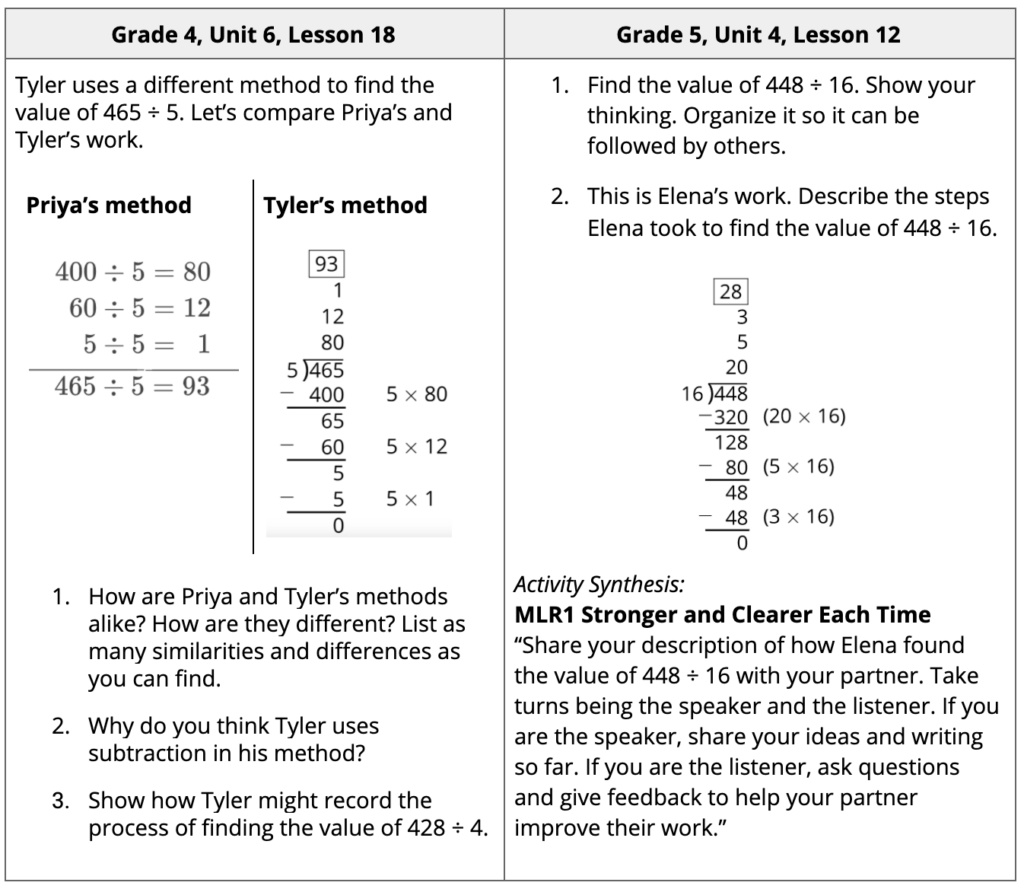
In the Grade 5 example above, students have the opportunity to engage in the Mathematical Language Routine Stronger and Clearer Each Time, in which they get immediate feedback from their peers on their developing ideas. This routine is not only a powerful way for students to develop their academic language, but to also collaboratively solidify conceptual understanding of complex topics, both of which help foster positive mathematical identities. Mathematically, students come to see that some decompositions may be more helpful than others for finding whole-number quotients. They can use this insight to make sense of algorithms and use partial quotients that are more complex.
3. Students know and use the standard algorithm.
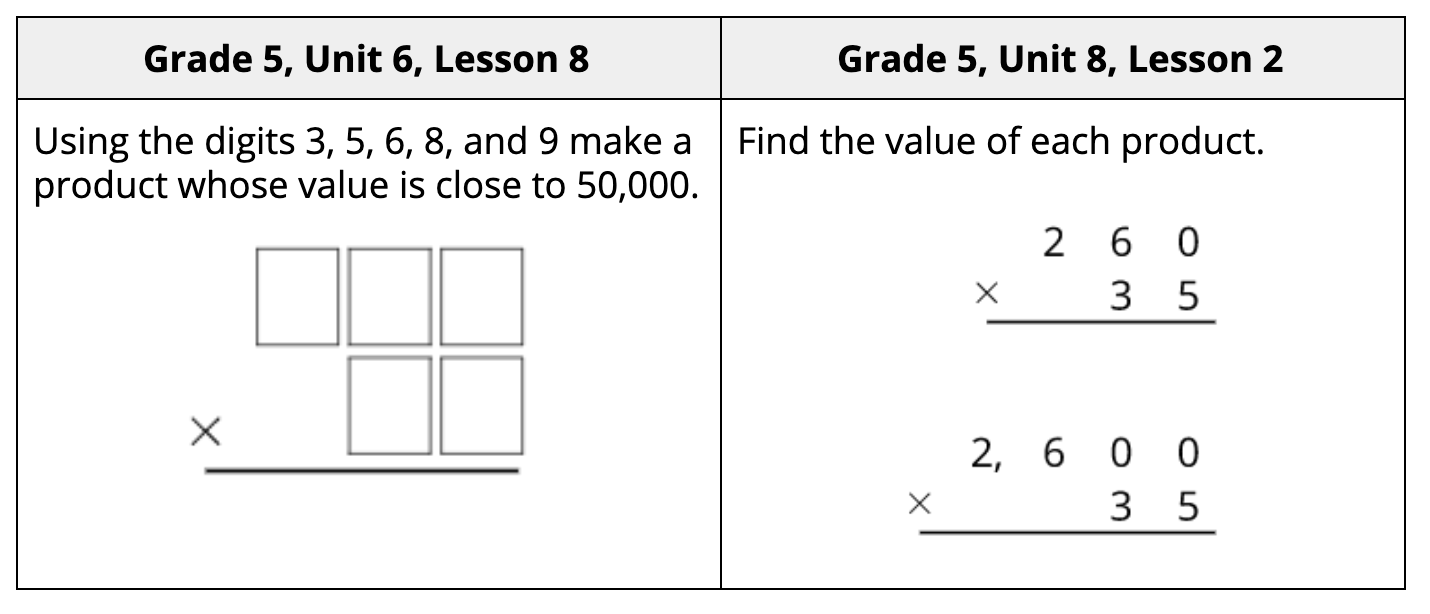
The algorithms using partial quotients in our Grade 4 and 5 courses follow a coherent progression that allows students to make sense of the standard algorithm for division that they will learn and come to know in grade 6. To meet the grade 5 requirement of fluency with the standard algorithm for multiplication, students have opportunities to practice the algorithm in Units 6 and 8 of our Grade 5 course.
Assessing Fluency Development
Teachers can use the look-fors on our section-level monitoring sheets to track student progress with fluency development. Looking across the grades, this tool shows how students transition from operating in ways that make sense to them to using and knowing the standard algorithm.
Maintaing Flexibility with Mental Math Strategies
Even with a deep focus on the progression towards fluency with the standard algorithms, IM K–5 Math continues to offer students opportunities to practice their facts and demonstrate flexibility with multiplication and division through instructional routines.

In this video clip, Savannah Sanders, a fourth grader in Saugus, CA explains how she efficiently reasoned through 15 x 40, the last expression in the Number Talk shown.
As a fourth grader, Savannah can use diagrams and written methods to solve problems like 15 x 40, but these Number Talk routines help students to think flexibly about the facts they know to compute mentally using their conceptual understanding of place value, the properties of operations, and the relationships between operations.
As students become comfortable with using mental strategies and the standard algorithms, they are able to determine whether it is appropriate to use the standard algorithm to find the value of a given product or quotient, or if a different strategy is more efficient.
A Gateway for Fluency, Conceptual Understanding and Positive Mathematical Identities
In this four-part blog post series we have shown our curriculum to be a coherent progression of concepts within and across grades, leading to fluency in the four operations with facts and algorithms. We have also shown how the curriculum’s problem-based structure creates a gateway for students to engage in mathematics in rich and meaningful ways. Our intentional design supports students to connect the ideas they already have to new learning, engage as doers of mathematics, and develop positive mathematical identities.
Next Steps
Take a look at the story of decimals in the curriculum in grades 4–6 to see if you notice a similar progression towards fluency with the standard algorithms for decimal operations.
In case you missed it, read part 1 and part 2 on fluency addition and subtraction and part 3 on fluency multiplication and division. You can also learn more about fluency in IM K–5 Math™ on the IM website.
Download our Fluency Development ebook, and use it as a resource to support students’ confidence in their execution of skills with a purpose.
