“The idea of being a ‘math person’ is based on two pervasive world views; first, the so-called ‘fixed’ mindset, that what one knows about math cannot change meaningfully over time through study and practice. Second, it is based on a narrow understanding of what it means to know and do math; ‘being a math person’ means memorizing formulas, computing quickly in your head, and being fluent with algebraic procedures only.”
Rolanda Baldwin, “What’s Your Math Identity?” (2020)
When designing IM K–5 Math™, we thought deeply about the potential impact of our curriculum on students’ mathematical identities. We believe all students have valuable experiences and ideas, and the capacity to learn grade-level math. Throughout each course, as students develop their understanding of what it means to know and do math, they have opportunities to compute in ways that make sense to them, build their knowledge of concepts through analysis and collaboration, and apply their knowledge to compute with accuracy, flexibility, and efficiency.
In this post and the one that follows, we intend to share how students’ mathematical identities play a role as they develop multiplication and division fluency within and across grades 2–5. In our last two posts—part 1 and part 2 on fluency development in addition and subtraction—we focused on addition and subtraction fluency development across grades K–5. We highlighted the processes for developing fluency with math facts and algorithms. Here we will show how these processes are evident in the design of the curriculum for developing fact fluency with multiplication and division.
Fluency with Multiplication and Division Facts
By the end of grade 3, students develop fluency with multiplication and division facts within 100. As shown in the table, the process of developing this fluency begins in grade 2 as students work with equal groups and arrays.
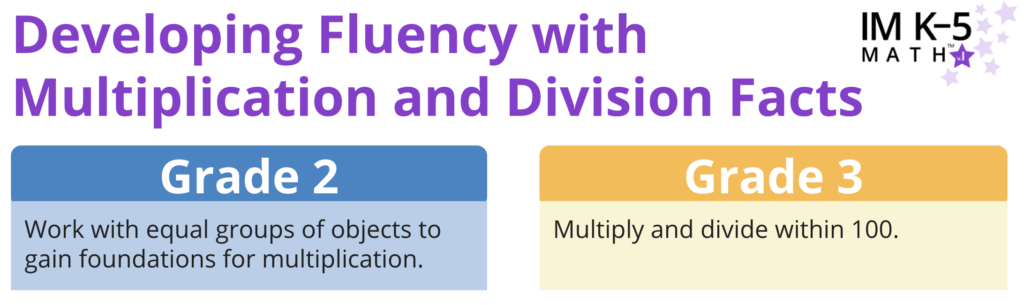
Much like in the story of addition and subtraction, fluency with multiplication and division facts is developed through an intentionally coherent process in IM K–5 Math™.
- Students learn the meaning of the operations and the relationships between them.
- Students start to learn their facts.
- Students relate more complicated facts to simpler ones.
- Students know their facts.
During this process, students have opportunities to learn new concepts by building from what they already know, which is the nature of our problem-based curriculum. Our intention is that through these experiences, they begin to see themselves as valued contributors to the progression of learning in their classrooms and develop positive mathematical identities.
Below, we analyze student work from beta pilot classrooms at each stage of the process. By doing so, we can get a sense of how fact fluency and mathematical identities can be developed with IM K–5 Math™.
1. Students learn the meaning of the operations and the relationships between them.
Beginning in grade 2, students work with equal groups and sums of equal addends to build a foundation for understanding multiplication and division in grade 3. In the IM K–5 Math™ Grade 2 course, this work starts in Unit 8. Students first make sense of equal groups through a study of odd and even. They then use their developing understanding of equal groups to learn about arrays.The problem below is from Lesson 7, the first lesson on arrays. To offer students space to make sense of new ideas, they may represent their thinking in different ways. IM Certified Facilitator Maureen O’Connell taught this lesson to a group of second graders in Ipswich, MA. The table displays the work of four of her students
In the example above, each student created an array with 4 rows and a total of 20 counters. Because they could use what they already knew to respond in ways that made sense to them, students represented their arrays by drawing counters or using physical objects. Student A used notation that showed how they counted the number of rows, while Student B shared that their prior knowledge of skip-counting helped them draw the array with 5 in each row. During the activity synthesis, students are invited to share their developing thinking about the structure of arrays, and begin to recognize that 20 can be made with a sum of equal addends, 5 + 5 + 5 + 5.
Looking back at the prompt, only one student, Student A, has a written response to the question, “How many counters are in each row?” The activity synthesis also suggests that teachers ask this question to uncover student thinking. While the focus of this question is to help students understand the structure of arrays as having the same amount in each row, students begin to develop ideas about equal groups, which will support understanding of multiplication in grade 3. This question also serves as a precursor to understanding the relationship between multiplication and division.
2. Students start to learn their facts.
Students start to learn their facts as they develop an understanding of the meaning of multiplication. In Unit 1 of Grade 3, students learn that multiplication can mean finding the total number of objects in a groups of b objects each, and can be represented by a x b. To build from what students know about skip-counting from earlier grades, the curriculum starts grade 3 students with learning twos, fives, and tens.
In the example below from the beta pilot, students from Andrea Welch’s class in Ipswich, MA make sense of a diagram showing 5 groups of 3. While both students write an equation with a symbol for the unknown and find the correct solution of 15, their reasoning is very different. Student A relates 5 x 3 to the sum 5 + 5 + 5 = 15. Student B decomposes 3 into 2 + 1, first counting each box by twos, then by one to get 10 and 5 more.
Without further investigation, one may conclude that both students are still developing an understanding that a x b represents a groups of b objects. Student A reasons about 5 x 3 using 5 + 5 + 5 instead of 3 + 3 + 3 + 3 + 3, and Student B interprets the diagram with 5 groups of 3 as 3 x 5 = 15 instead of 5 x 3 = 15. Students are not expected to adhere to the convention of writing a groups of b objects as a x b rather than b x a, but if they describe groups, they are expected to do so accurately. As shown in Student A’s work, knowledge of the commutative property starts to develop in Unit 1 of grade 3, and students are encouraged to use that reasoning to find products.
This next example is from the Grade 3, Unit 2 Adaptation Pack, which teachers used during the beta pilot to support unfinished instruction due to the pandemic. The lesson activity, which can be found in Grade 2, Unit 8, sets the stage for area understanding and a deeper understanding of multiplication. In working with arrays, this student from Amy Gookin’s class in Portland, ME begins to notice the commutative property of multiplication.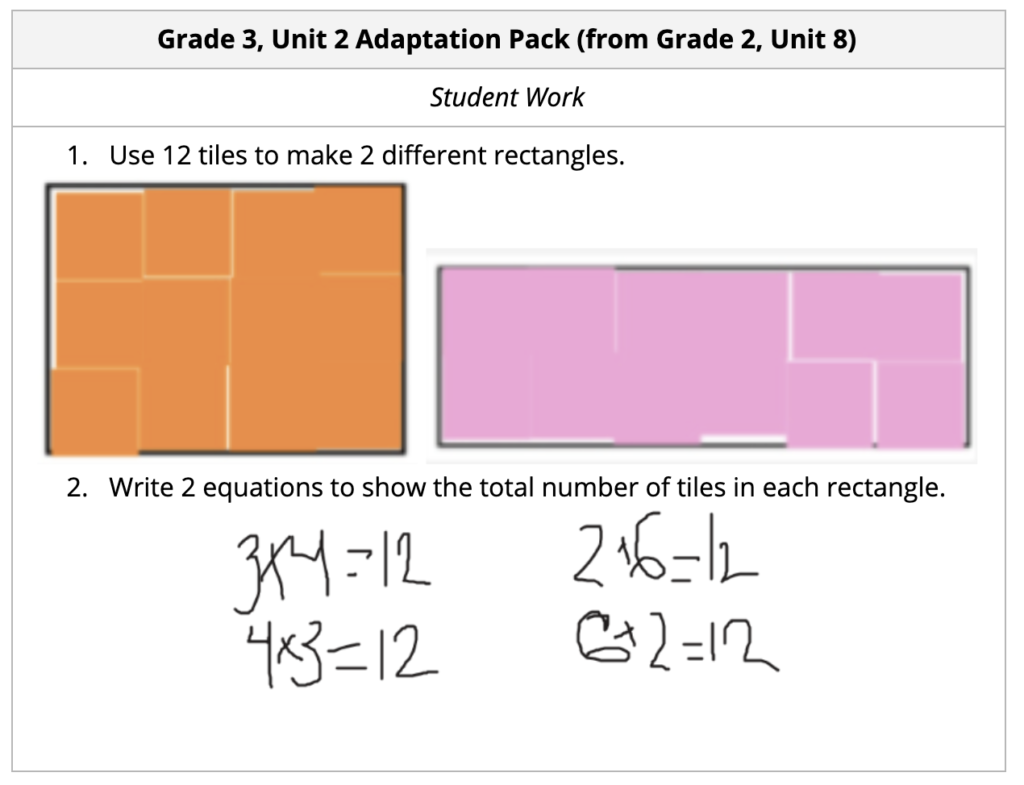
While grade 2 students would likely write equations involving sums of equal addends, grade 3 students can write multiplication equations when this lesson is positioned after an introduction to the multiplication symbol in Grade 3, Unit 1.
In Unit 2, students relate the area of rectangles to multiplication. They see that rectangles can be tiled with squares in equal-size rows (or columns), so if the rectangle is 3 units by 4 units, there are 3 groups of 4 tiles or 4 groups of 3 tiles. The number of square units is 12, which can be represented by the equations 3 x 4 = 12 or 4 x 3 = 12. In later lessons, students come to understand that multiplying the side lengths of a rectangle gives the same number of squares as counting them.
3. Students relate more complicated facts to simpler ones.
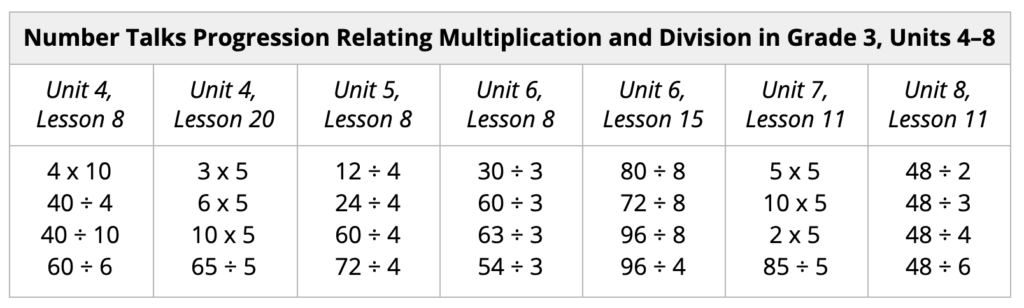
As students come to know some facts, they can use their conceptual understanding to learn new facts. The progression of Number Talks below highlights how students practice this skill in grade 3 to develop fact fluency.
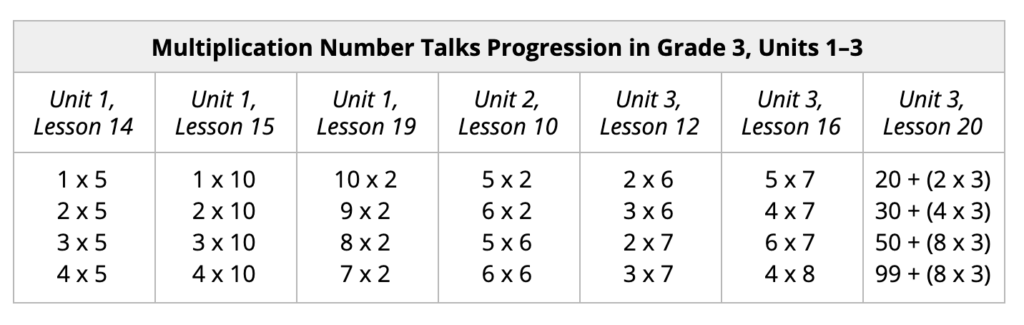After practicing their twos, fives, and tens, students conceptualize one more group, one less group, doubling, and halving to learn and practice their threes, fours, sixes, and then the rest of their facts.
In this example from Unit 4 Lesson 10, a grade 3 student from Amy Gookin’s class in Portland, ME finds 6 x 7 by decomposing (or breaking apart) the 7 into 5 and 2, and then adding the two products.
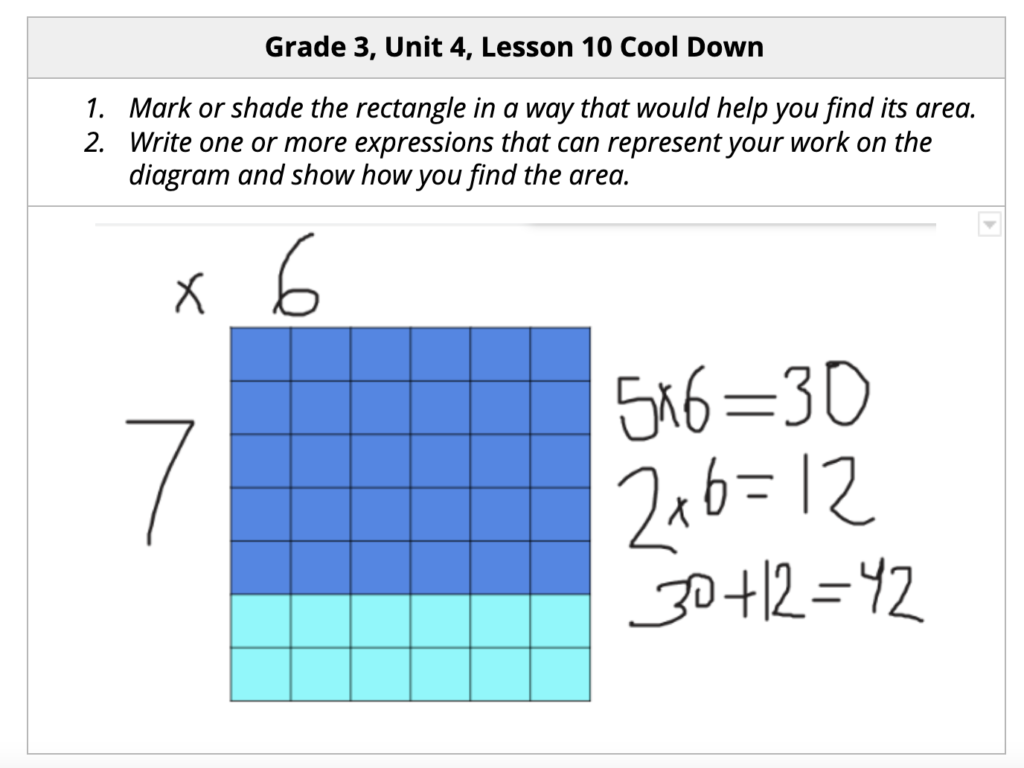The curriculum allows students to analyze and use area diagrams to develop understanding. This strategy of relating more complex facts to simpler ones becomes helpful as students learn to multiply larger numbers. A student from Tabitha Eutsler’s class in Springfield, MO, shared just that in an added reflection on this Lesson 13 cool-down.
Students begin to develop positive mathematical identities when we allow them to make sense of mathematics through problem solving, and give them space to use strategies that build from what they already know. The student above showed appreciation for a strategy that helped with efficiency. As students learn the importance of fact fluency, they develop a sense that certain strategies are more efficient than others. They become more confident when they can approach new problems and find solutions even when they don’t know all of their facts from memory.
Throughout Unit 4, students use the relationship between multiplication and division to develop fluency with multiplication and division facts within 100. By Lesson 20, students are using the strategies they know to divide larger numbers. Below, students from Maureen O’Connell’s class in Ipswich, MA show very different ways for finding the value of 80 ÷ 5.
The activity synthesis for the activity above asks teachers to consider polling the class on the strategy they used. This teacher move offers students a moment to deepen conceptual understanding of the relationship between multiplication and division, and the properties of operations. Connecting their strategies to those of their peers also gives students room to celebrate their thinking and see themselves as doers of mathematics. As students share and discuss strategies, they begin to make decisions about the strategies they would like to try, as some strategies may be more appropriate or more efficient than what they had previously used.
Deepening conceptual understanding in this way encourages flexible thinking. Students are eventually able to use these strategies mentally during instructional routines and centers. The Number Talk routines in the table below are strategically placed throughout the rest of the Grade 3 course to allow students to continue to practice these strategies and develop fact fluency.
4. Students know their facts.
Throughout grade 3, students may be in different places along the continuum of fluency. Some students may be more efficient with certain facts. As we mentioned in our earlier post about developing fluency with addition and subtraction facts, conceptual understanding can be developed as a foundation for fact fluency or even after fluency has been achieved.
During Unit 4, students sort facts cards and reflect on the facts they know right away and the facts they are still working on. They continue to use these cards throughout the year to intentionally practice their facts and monitor their own progress. (Read more about how students come to know their multiplication facts in this post.)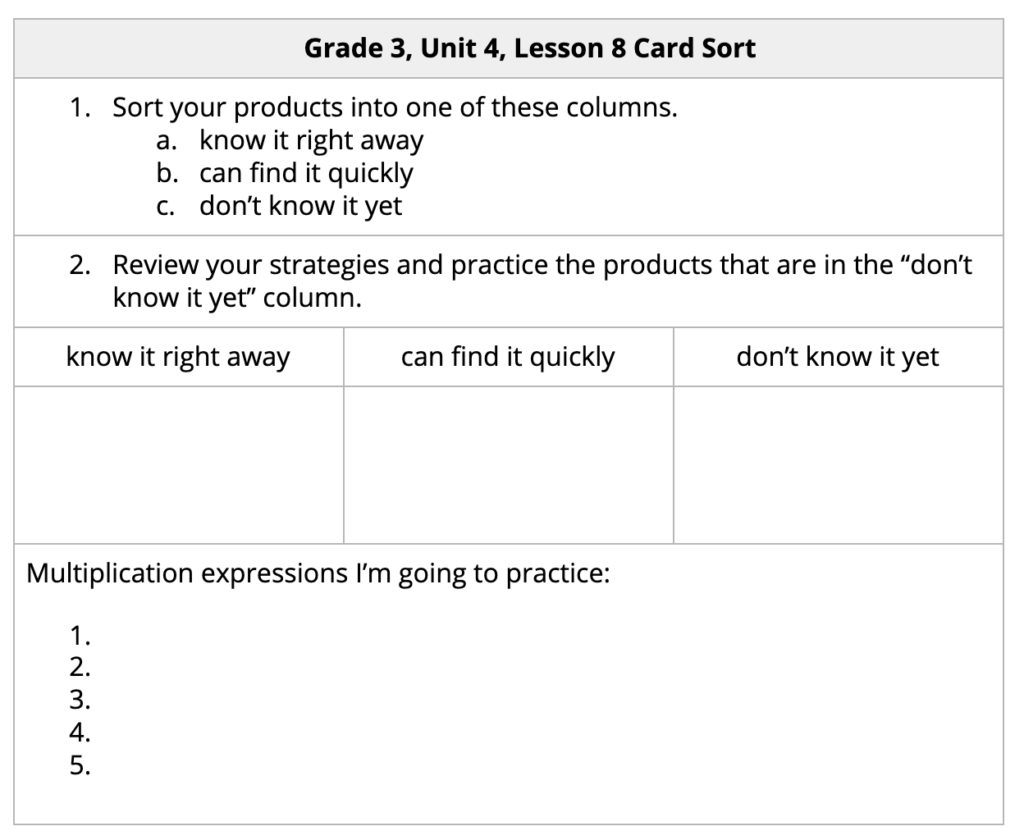
As they practice their facts and develop fluency during lessons, centers, and warm-ups, they take ownership of their learning and strengthen their mathematical identities. In the video clip, third-grader Viviana Ramirez from Katy, TX uses facts she knows from memory to accurately, flexibly, and efficiently divide within 100.
When Viviana pauses, she is taking time to think flexibly and use mental strategies. These pauses signal perseverance, and should not be characterized as having a lack of division fluency. Her perseverance is evidence of a positive mathematical identity, as she believes that she is capable of arriving at a correct response on her own, given time to think it through. The joyful smile on her face is also evidence.
Designed to Develop Positive Mathematical Identities and Fluency
Flexible thinking is important for the development of positive mathematical identities. Opening up activities and discussions to include different ways of thinking gives students freedom to explore their ideas. Students build confidence as they practice using strategies based on their prior and developing knowledge of numbers and operations.
While it remains to be seen if each student who goes through our courses will eventually identify as a “math person”, we are confident that our intentional design will help students realize that they already have important mathematical ideas that they can use to solve problems and learn new mathematical concepts.
Next Steps
For more on multiplication fluency, read this post by Grade 3 Lead Author, Zack Hill.
How do students develop fact fluency with addition and subtraction? This post is part 3 of a four-part series on developing fluency with IM K–5 Math™.
In case you missed it, read part 1 and part 2 on fluency development in addition and subtraction, and part 4 on fluency multiplication and division. You can also learn more about fluency in IM K–5 Math™ on the IM website.
Download our Fluency Development ebook, and use it as a resource to support students’ confidence in their execution of skills with a purpose.
