Dionne Aminata, Senior Director of Strategic Initiatives, Marketing, Illustrative Mathematics
Rolanda Baldwin, Vice President of Mathematics, UnboundEd
Illustrative Mathematics and UnboundEd both agree that achieving racial justice in math education starts with the belief that all students are deserving, capable learners of grade-level mathematics.
Illustrative Mathematics (IM) is a non-profit organization with a vision of creating a world where all learners know, use, and enjoy mathematics. Decades of mathematics achievement data show significant racial disparities that indicate an unjust educational system, where Black and Brown students in classrooms across the United States have unequal access to mathematics learning. IM is committed to racial justice through ensuring the right of every learner to engage in meaningful, rigorous, grade-level mathematics. Equipped with high-quality instructional materials such as IM K–12 Math™, teachers implementing culturally responsive pedagogy have the potential to disrupt pervasive inequities in the kinds of mathematics education that students receive.
UnboundEd is a national non-profit, dedicated to empowering educators to actively work together to dismantle systemic racism by providing grade-level, engaging, affirming, and meaningful (GLEAM™) instruction.

Through years spent working in schools, developing immersive professional development experiences, and delving into available research, UnboundEd has created a framework that articulates a vision for cultural responsiveness. UnboundEd’s GLEAM™ Instructional Framework encompasses a hypothesis about what it takes to bring this vision for teaching and learning to life, based on the research of Dr. Gloria Ladson-Billings, Geneva Gay, Zaretta Hammond, D’Jango Paris and others: student experiences and teacher actions are concrete products of teacher mindsets and planning practices.
UnboundEd’s GLEAM Hypothesis
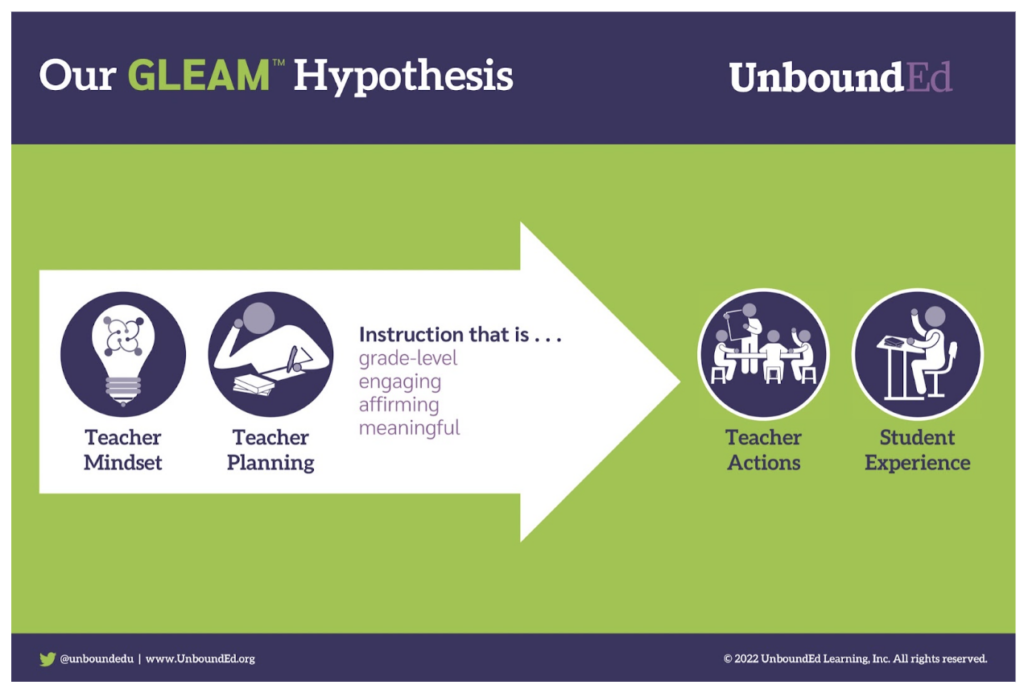
What does it take for students to feel that their cultural funds of knowledge are affirmed in the course of instruction, or to see how what they are learning can be used to challenge inequity? According to UnboundEd’s GLEAM hypothesis, engaging, affirming, and meaningful grade-level instruction happens when teachers both know the grade-level academic standards, and consider those standards within the context of their students’ cultures.
IM K–12 Math represents exactly the sort of high-quality, standards-aligned curriculum that lies at the center of UnboundEd’s GLEAM hypothesis. UnboundEd’s instructional framework emphasizes that cultural responsiveness in the classroom comes from the skilled work of educators adapting standards-aligned curricula. IM’s high-quality instructional materials are well-suited to support these aims. IM K–12 Math is designed in such a way that teachers can implement it with integrity while adapting it to meet the academic and cultural needs of their students.
Let’s take a closer look at how IM K–12 Math and UnboundEd’s GLEAM instructional framework can work together.
Grade-level Learning
IM K–12 Math is aligned to state standards and has been given the stamp of approval by EdReports, earning perfect scores in the areas of Focus & Coherence and Rigor & Mathematical Practices. UnboundEd’s GLEAM instructional framework includes planning practices grounded in the Mathematical Shifts of Focus, Coherence, and Rigor. With IM, students experience courses that focus on the major work of each grade, and have thoughtful connections to supporting and additional concepts within and across grades. Units and lessons follow a coherent progression of learning, which allows students to build new learning from their prior mathematical knowledge.
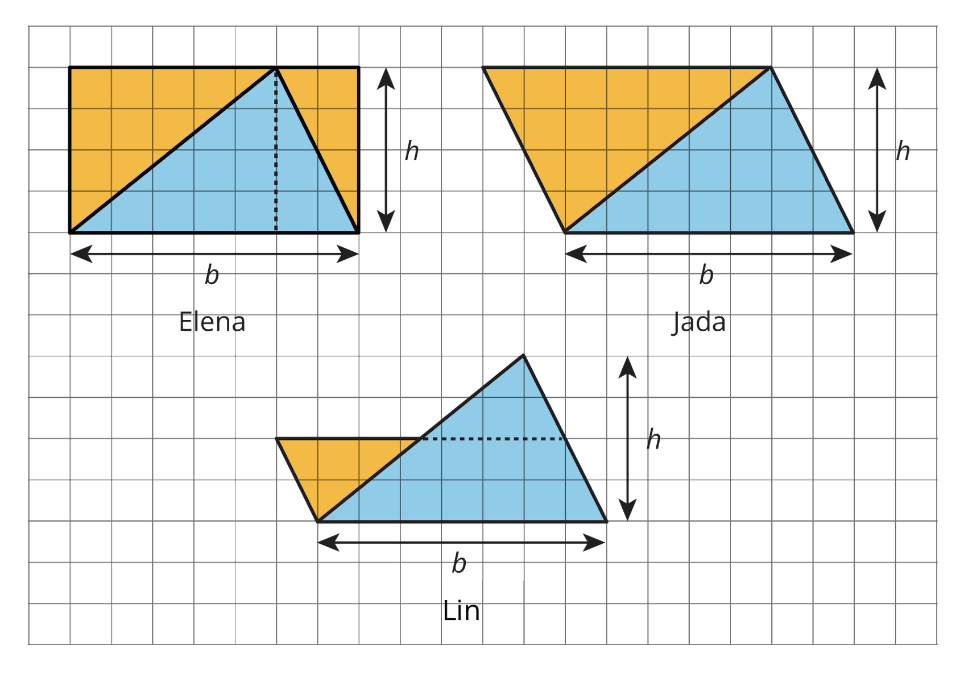
For example, in Grade 6 Unit 1 Lesson 9, students write and use a formula to find the area of triangles. In prior lessons within this unit, students reinforce their understanding of area from earlier grades, including that area is additive. They learn that a two-dimensional region can be decomposed into smaller pieces and rearranged, while maintaining its area. They then take these insights to relate triangles to parallelograms and find the area of parallelograms, all before experiencing Lesson 9.
During the warm-up of Lesson 9, students analyze examples and non-examples of the base and the height of triangles to invite students to think about the meaning of these terms. Students then begin to reason about the area of triangles using their conceptual understanding of the area of parallelograms from previous lessons. As the lesson progresses, they write an expression that could be used to find the area of any triangle, and apply this formula to find the area of more triangles.
Educators using UnboundEd’s GLEAM framework continuously seek knowledge of content and pedagogy. IM K–12 Math teacher-facing materials are purposefully designed to develop teachers’ mathematical content knowledge and their ability to respond to student thinking. These materials are educative for teachers, in that they provide descriptions of the progression of learning within each unit, section, and lesson to help teachers know what to look for in student work, and discourse questions for teachers to ask students during the lesson to assess or advance student understanding as they work towards the lesson’s learning goals.
Ensuring Engagement
As noted above, UnboundEd’s definition of engaging instruction is persistence in grade-level work that builds students’ interests and ties to knowledge and culture without disrupting their beliefs about who they are, where they come from, and what they can become. In IM K–12 Math’s problem-based instructional model, where students learn math by doing math, there are significant opportunities to build engagement in the way UnboundEd has defined. Before diving into tasks, especially those with unfamiliar contexts, IM materials offer launch activities or whole-class discussions to activate students’ current mathematical knowledge, and honor students’ voices, language, and funds of knowledge.
Grade 3 Unit 1 Lesson 10 introduces the concept of multiplication using a scaled picture graph of different types of road signs. To provide students with an opportunity to connect to this context, the launch activity is a Notice and Wonder about the graph, where students can think about the types of road signs they have seen in their community and connect with the context. Launch activities can help students bring their whole selves to the lesson, as they make mathematical connections between the concepts they are learning and their everyday lives. Activities like this aid in planning for GLEAM instruction.

Affirming All Learners
According to UnboundEd, affirming instruction honors and acknowledges students’ ethnic, racial, cultural, and linguistic identities and experiences within the context of grade-level work.
IM K–5 Math (and soon IM’s secondary materials) supports UnboundEd’s GLEAM hypothesis by providing mathematically appropriate tasks that are relevant to and reflective of the lived experiences of Black and Brown students, which benefits all students. Tasks such as these positively represent marginalized cultures through a mathematical lens. These experiences can encourage discourse that is both mathematical and affirming of the ethnic, racial, and cultural identities of all students in the classroom.
For instance, in Grade 4 Unit 6 Lesson 13, students learn about division with remainders using the context of sharing snacks with the class. To launch into this activity students think about their favorite snacks, then they solve problems involving sharing paletas from Mexico, gulab jamuns from South Asia, and chocolate-covered breadsticks from East Asia. This lesson also includes teacher reflection questions that support teachers to think about the connections students were making between the context of the problems and the concept of division. This design directly supports teacher planning in service of GLEAM.

In all courses K–12, IM honors students’ linguistic identities by offering access to grade-level mathematics through Math Language Routines. In Algebra 2 Unit 4 Lesson 6, students apply their understanding of exponential functions to solve problems using the Information Gap routine. Through discourse, students can use informal and developing academic language to work collaboratively to solve complex problems. This lesson also embeds the Stronger and Clearer routine, which helps students fine-tune their academic language as they have multiple opportunities to get feedback from their peers, and write stronger and clearer explanations of their work.
Making Math Meaningful
Within UnboundEd’s GLEAM instructional framework, meaningful instruction happens when teachers support students to understand and critique dominant cultural norms and examine their community’s social position to foster a sense of advocacy and change. IM K–12 Math enables educators to offer their students these opportunities for examination and critique of the world around them.
For example, in Geometry Unit 2, after Lesson 1, students can engage in the modeling task, “How Much Water?” where they examine their personal water consumption in a day, week, month, and year, and think about the number and size of containers that could hold that amount of water. Teachers who have done the work to build their cultural knowledge of their students, families, and communities can adapt tasks to support students to examine and challenge inequity, and advocate for change.
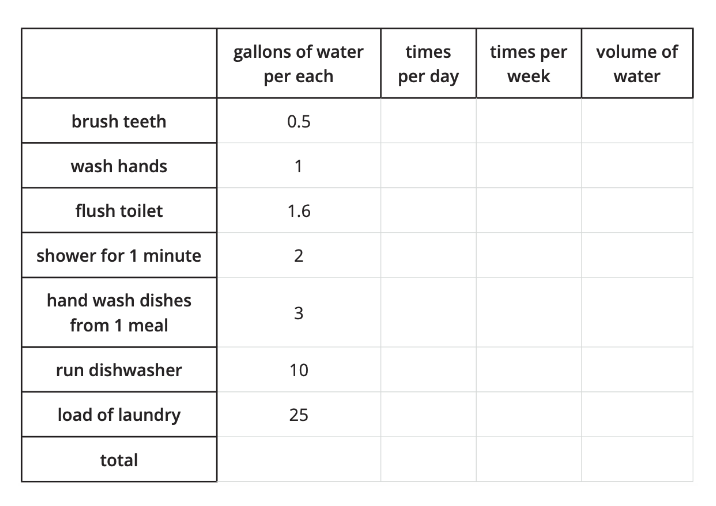
To extend this modeling task, for example, teachers can ask students to research the size and number of water bottles that families were given during the water crisis in areas such as Flint, Michigan, determine whether they were given a reasonable number of water bottles, and spark discussions about what students can do to advocate for these families and affect change. Adaptations like these are supported by IM’s design and are in line with UnboundEd’s GLEAM hypothesis.
Answering the Call
As teachers and leaders work together to help achieve racial justice in math education, there is a need for clarity and support. As UnboundEd has defined in its GLEAM instructional framework, providing instruction that is grade-level, engaging, affirming, and meaningful is the skilled work of educators as they make sense of and adapt high-quality instructional materials. Illustrative Mathematics provides high-quality, standards-aligned materials that are uniquely appropriate to work with the GLEAM instructional framework. They challenge teachers to reflect on their practices to ensure equitable access to grade-level mathematics and encourage thoughtful adaptation to make instruction culturally responsive. Illustrative Mathematics and UnboundEd make a powerful pairing to disrupt the inequities that have long characterized math instruction in this country.
Next Steps
To learn more about IM K–12 Math™, visit https://illustrativemathematics.org/math-curriculum.
To learn more about UnboundEd’s GLEAM™ instructional framework, visit https://www.unbounded.org/blog/what-is-gleam.
