Deepa Bharath, District Instructional Lead Teacher, Mathematics at Cambridge Public Schools
Sarah Caban, Interim Director, K–5 Teacher Learning at Illustrative Mathematics
“Illustrative Mathematics is a problem-based curriculum that fosters the development of mathematics learning communities in classrooms, gives students access to the mathematics through a coherent progression, and offers teachers the opportunity to deepen their knowledge of mathematics, students’ thinking, and their own teaching practice.” — from the K–5 IM v.360 course guide
Teaching in a problem-based classroom is complex. During any given lesson, teachers actively listen and ask questions to gauge students’ thinking while simultaneously making in-the-moment decisions about how to leverage that thinking to advance collective learning. To support teachers in this work, certain activities in the IM curriculum are labeled as “recommended for study” in a professional learning community (PLC). These activities either highlight key mathematical ideas or require complex facilitation.
In the IM curriculum course guide, there is a recommended structure for teachers to follow when using a PLC activity within their professional learning communities. The structure promotes opportunities for teachers to plan, rehearse, teach, and reflect together. Recently, Deepa Bharath, the district instructional lead teacher of mathematics for Cambridge Public Schools had the opportunity to use one of the PLC activities with a group of fifth-grade teachers and coaches.
Below, Deepa provides a personal account of how this PLC activity unfolded, offering insights into its impact on teacher learning and instructional practice. Her reflections demonstrate the ways that professional learning communities promote opportunities for teachers to deepen their knowledge of mathematics, students’ thinking, and their own teaching practice.
Before the Professional Learning Community Meeting:
Our district has been using our professional learning community spaces to explore what it means to teach the IM curriculum with integrity. We are engaging in intentional conversations about when and how to make adjustments that deepen the exploration of important math ideas without compromising the curriculum’s learning goals and design structure.
Recently, a group of eight fifth-grade teachers and coaches from two schools met to co-plan, co-teach, and debrief a lesson together. To prepare for the day of learning, I read the teacher-facing materials for Grade 5 Unit 4 Lesson 10 Activity 1.
The Launch of the activity asks students what they notice and wonder about a set of division expressions. I laid out the 32 division expression cards for Activity 1 and considered, “What do I notice? What do I wonder?”

My first thought was, “Wow, that’s a lot of cards. How do we facilitate a notice and wonder with the whole class? What might students say?” As I began to organize the cards, I noticed many patterns. I could not remember a time when I had to look at so many division expressions at once. I began to wonder about the intentional choices for the numbers in the expressions. I knew then that providing teachers time to explore the cards would not only deepen our own understanding of division but also enhance our ability to anticipate students’ thinking.
During the Professional Learning Community Meeting:
Teachers and coaches worked in groups of two to examine the division expression cards and then shared their noticings and wonderings with the whole group. I encouraged them to elaborate on their thinking and make connections between their observations:
Teacher 1: Many dividends are friendly numbers.
Deepa/facilitator: Could someone give some examples of “friendly numbers” in the cards? How else might students describe friendly numbers?
Teacher 2: Numbers that are multiples of 10 such as 140 or 300.
Teacher 3: Some expressions are the same, such as 100 ÷ 14.
Teacher 4: We noticed 8 ÷ 14 is the only single-digit dividend in the expressions.
Teacher 5: Divisors are all 14.
Teacher 6: We noticed that some expressions are easy to compute mentally, for example 14 ÷ 14 = 1, and since we know 14 x 2 = 28, 28 ÷ 14 = 2. That helps us with 140 ÷ 14 and 280 ÷ 14.
Teacher 4: Would students use the same language we did? It would be great if they could use this math vocabulary in their notice and wonders.
Teacher 3: I know that (70 ÷ 14) + (70 ÷ 14) can help me think about (140 ÷ 14).
Deepa/facilitator: Let’s pause here. Turn and talk to your partner about why that works and how you might convince yourself or someone else to understand why (70 ÷ 14) + (70 ÷ 14) = 140 ÷ 14? What example, context, or visual might you use?
Teacher 2: I had a hard time convincing my partner why it works. She wondered why (70 ÷ 14) + (70 ÷ 14) wasn’t (140 ÷ 28).
Teacher 1: Well, I used the Peruvian folk dance context, which students know from the previous lesson. If 70 dancers made groups of 14 and another 70 dancers made groups of 14, we have a total of 140 dancers, but the group size is still 14. That hasn’t changed!
Teacher 2: So if I had 140 M&Ms to divide among 14 people, I can get 70 first, divide that among the 14 and then take another 70 and divide that.
Teacher 5: I tried to draw an area model, but I’m not sure it’s accurate.
Having come to a consensus around what the area model might look like, I asked, “What are we thinking in terms of how we facilitate Activity 1 with students?” One of the teachers who had already taught Lesson 10 chimed in: “I wish I had given my students more time to study the cards and share their noticings as a whole group. I think it would have made the discussion richer and provided more access to the question they are asked in Activity 1.”
Activity 1
Take turns:
- Choose a set of expressions that when added together have the same value as 308 ÷ 14. Not all expressions will be used.
- Explain to your partner how you know that your cards represent a sum that has the same value as 308 ÷ 14.
(Pause for teacher directions.)
- Choose one of the sets of expressions. Use it to find the value of 308 ÷ 14.
We decided to try the teacher’s recommendation. We agreed to give the students extra time for the Launch in service of providing more access to the problems in Activity 1. During the Launch, students had 5-8 minutes to look at the cards with a partner and discuss what they noticed and wondered while the facilitating teachers listened and recorded their observations and questions on a chart.
Students’ noticings and wonderings were similar to the teachers. They noticed two-digit, three-digit, and single-digit dividends. Some students were treating the cards as “flash cards” and trying to find the value of the expressions. We reminded them to just notice and name some patterns.
Next, we invited students to work with their partners to complete the tasks in Activity 1. As we monitored students working in their partnerships, we noticed them choosing sets of expressions that we had anticipated, such as these:
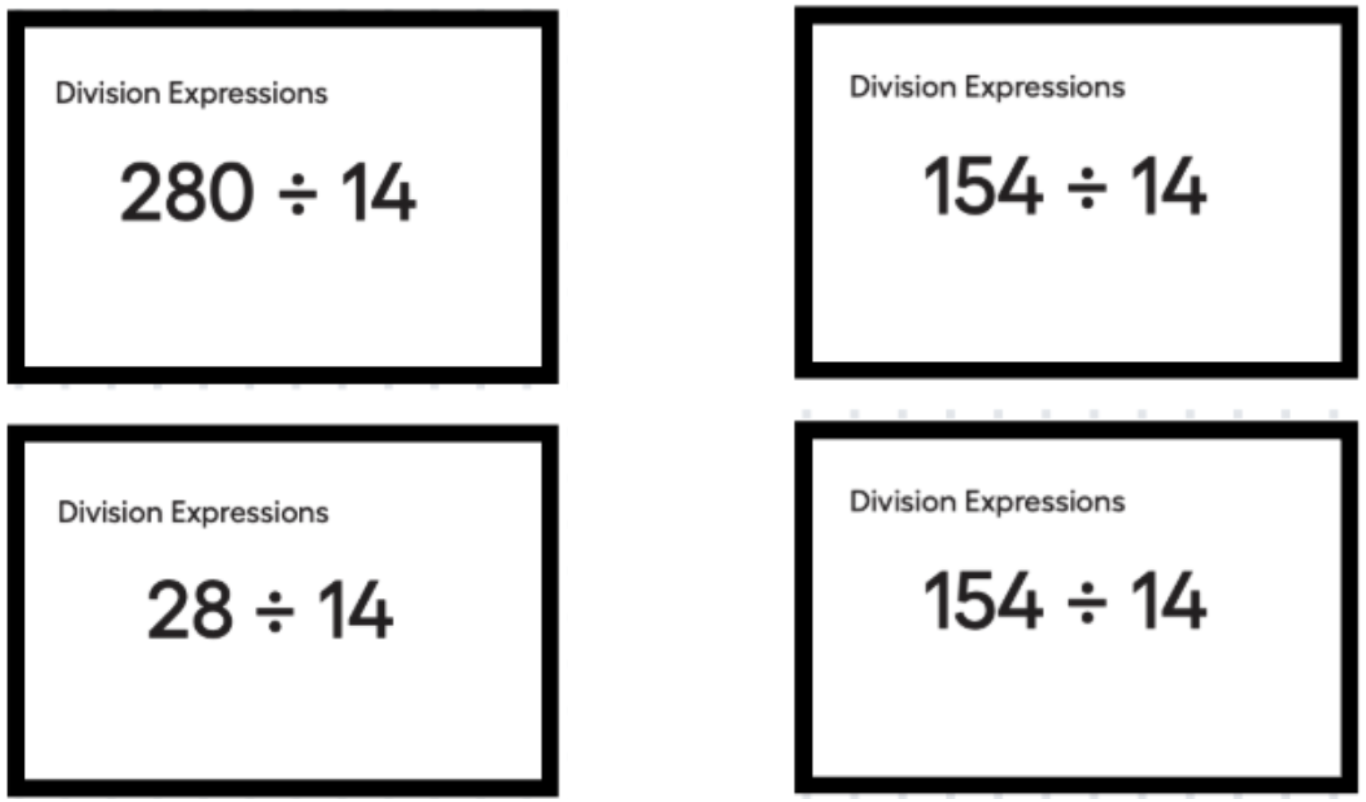
We also had a lovely surprise we had not anticipated. One student chose these expressions to find the value of
308 ÷ 14:
(300 ÷ 14) + (28 ÷ 14) – (20 ÷ 14)
Another student was confused: “Wait! That can’t work! Could it? I mean . . . I know 308 ÷ 14 is 22 because 280 ÷ 14 is 20 and 28 ÷ 14 is 2. But how could . . . two of the expressions have a remainder with decimals? How could that add up to 22?”
We had not expected this! It was truly an exciting moment, even though we were not quite sure how to address the student’s question in-the-moment. We realized we needed more time to make sense of the student’s question, explore the math further, and consider how to respond. We said, “Let us think and get back to this question tomorrow.”
After the lesson, we spent some time reflecting on what we noticed during the lesson and what we still wondered. When I got home that night, I was still wondering about the student’s question and decided to do some math. The curriculum had not introduced students to division with decimals yet, but students had explored the relationship between division and fractions in an earlier unit. Thinking about division as fractions helped me avoid the messiness of decimals.

Planning, doing the math, and teaching this lesson pushed my thinking. I found myself flexibly shifting between division and fractions to make sense of partial quotients. What would happen if students saw my work? How might it influence the ways they solved 308 ÷ 14? The next day, I shared my work with students and invited them to notice and wonder about my strategy. A few of them even tried it out. Take a look!
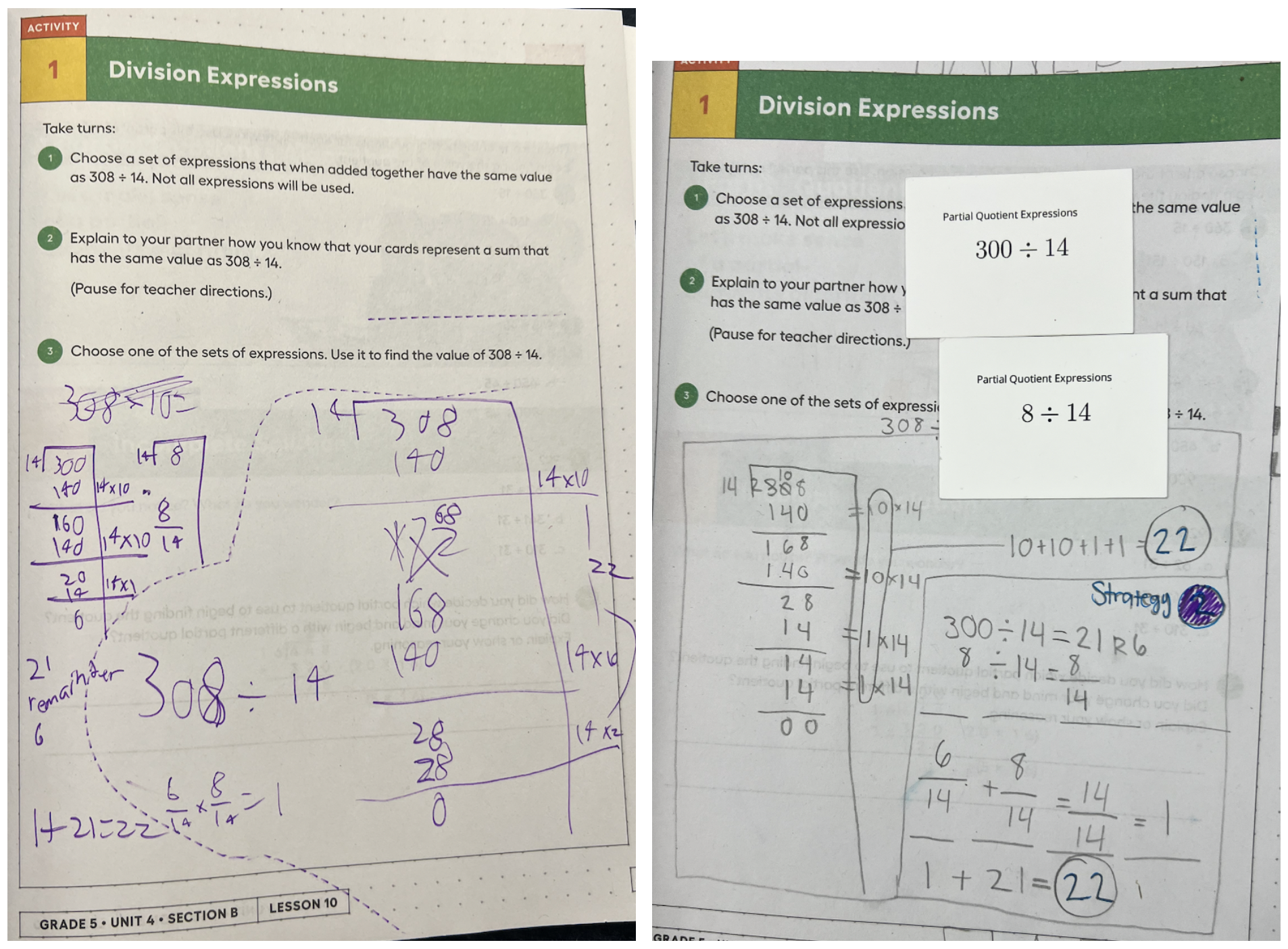
Conclusion:
Deepa and her colleagues leveraged their professional learning community. They did math together, made mistakes, asked questions, and embraced the discomfort of unanticipated questions. Teaching is complex, requiring countless in-the-moment decisions. Professional learning communities create space for educators to pause and linger in those moments together—deepening our knowledge of mathematics, students’ thinking, and our own teaching practice.
Next Steps/Call to Action:
- How are you using the PLC activities in the IM curriculum to teach and learn together? Let us know!
- Feel free to use or customize this sample agenda for your next PLC meeting.

Deepa Bharath
District Instructional Lead Teacher, Mathematics at Cambridge Public Schools
Deepa Bharath (she/her) serves as a district instructional lead teacher (JK–5) in Cambridge Public Schools. Deepa’s career includes roles as a special education teacher, mathematics coach and professional learning consultant. Deepa is passionate about uncovering math traditions from diverse cultures and celebrating the richness of informal mathematics embedded within our families and communities. She believes that highlighting these connections not only broadens our understanding of mathematics but also nurtures school communities, where everyone feels a sense of belonging in math.

Sarah Caban
Interim Director, K–5 Teacher Learning at Illustrative Mathematics
Sarah was one of the lead authors of the Grade 5 curriculum for Illustrative Mathematics K–5 Math, and she is currently the interim director of K-5 teacher learning at Illustrative Mathematics. Sarah collaborates within and across teams to develop professional learning experiences that position teachers and students as authors of important mathematical ideas.
