By Jenna Laib
My sixth graders are weary of pre-assessments.
No matter how many times we discuss the goal of a pre-assessment–for me to learn more about their current strategies and understandings, so that I can design learning experiences that fit them better–all of them seem to want to impress me with perceived “perfection.” (As flattering as this is, they are missing the point.)
With this in mind, I wanted to design a series of formative (pre) assessments that look less like a test and more like one of our typical class activities. These assessments would need to have several entry points, allow me time to observe student strategies, and (with fingers crossed) start a few math debates that would set the stage for us justifying our reasoning and critiquing the reasoning of others throughout the unit.
Planning Task #1: The Clothesline
That’s when I stumbled upon Tamara DeFord’s blog post about the intersection of fraction talks and clothesline math:
I selected several images from Fraction Talks–all designed from the same unit square–representing a range of difficulty.

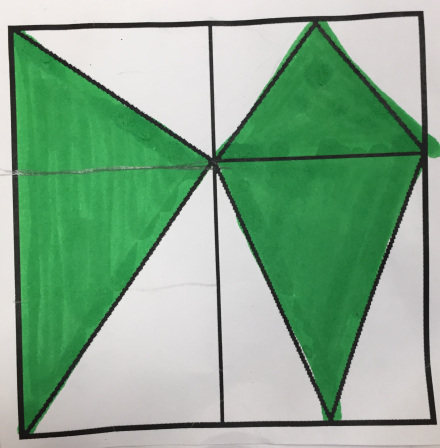
Anticipating
After selecting the images, I designed an anticipation guide (a lá the five practices for orchestrating classroom discussion). I expected to see students:
- unitizing
- adding fractional pieces, e.g. $\frac14$ + $\frac{1}{16}$ + $\frac{1}{16}$
- subtracting fractional pieces (e.g. negative space)
- multiplying to find a portion of a known piece (e.g. $\frac34$ of $\frac14$ is colored in)
- using spatial relationships
- and goodness knows what else (tactfully identified as “other” as on my anticipation guide)
Here are links to the document detailing my anticipated strategies in word doc format and also PDF.
This anticipation guide focuses on the strategies students used to determine the value of the shaded spaces on the fraction talk images. This talk also involved determining how to place it on the number line.
Regarding the placement on the line, I anticipated that students would use
- benchmarks, e.g. of 0, $\frac14$, $\frac12$, $\frac34$ and 1
- convert to a decimal equivalent
- build from unit fractions (e.g. for $\frac38$, find $\frac18$ on the clothesline and then mark iterations of $\frac18$ using hands)
- ask for a standard measurement tool, e.g. ruler, yard stick, or meter stick
- other?
Almost all of my students relied on comparing fractions to a benchmark. In the photo below, you can see the two cards that are equivalent to $\frac14$ are exactly in the middle of 0 and $\frac12$ (some students did ask for measurement tools for this!), and they were able to approximate other cards from there. Because there was not as much diversity in their placement strategies, I choose to write about how they determined the value of the fraction talk image, which hints at their underlying reasoning about fraction size, relationships and also computation.
Enacting The Task

To introduce the task, I gave each student the same card–a relatively easy one representing $\frac{1}{16}$, seen in red in the above photo. Students worked independently to determine the value of the colored piece, during which time I conferenced with individuals to identify preliminary strategies. After two minutes, I broke them into groups to discuss strategies and placement on the number line. The students seemed to reach consensus quickly and easily, which meant we were ready to move on to the full task.
Groups of students were each given the same cards to place on the number line. The cards were color coded to facilitate comparisons between groups later in the lesson.
Monitoring: Listening to Student Strategies
While students worked, I circulated, conferenced, and recorded their strategies on my anticipation guide. For the blue card (see below), Caleb multiplied to find a portion of a missing piece (although it’s not clear he knew that he was multiplying), and subtracted negative space. Meanwhile, Lily unitized.

Caleb
“The blue one would be $\frac34$, but it’s missing $\frac14$ of $\frac14$. So it’s missing a $\frac{1}{16}$.
$\frac34$ – $\frac{1}{16}$ is like doing $\frac{12}{16}$ –$\frac{1}{16}$, which is $\frac{11}{16}$.”
Lily
“The blue one is missing a piece. I can split the entire square into pieces that size. You can see that they’re sixteenths. The top left fourth has $\frac{4}{16}$, and the bottom right has $\frac{4}{16}$, too. So that’s $\frac{8}{16}$. I’m already past $\frac12$. Then the bottom left fourth has $\frac{3}{16}$, so that’s 4 + 4 + 3 = 11. It’s $\frac{11}{16}$ in all.”
How much is the milk carton worth?
To close our lesson, I asked students to share their reasoning around the orange card, a point of contention for several groups. Rayna referred to it as the “milk carton problem,” based on its shape, and the name stuck.
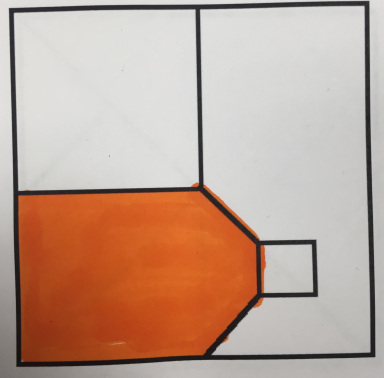
Students offered several different fractions to represent the area: $\frac16$, $\frac{5}{16}$, $\frac{11}{36}$…
Monitoring
There were students that had successfully solved it using unitizing, addition, multiplication, and a combination thereof. I gave students a minute to map out their argument, and then we began the Great Milk Carton Debate.
Selecting and Sequencing
I had monitored students working on this card in particular, and selected three students to share their thinking. Some of my students seemed rigid in their strategies, only using unitizing. They would tile the plane with the smallest recognizable piece, and then compose the larger shapes from there. I wanted them to see how they could use unitizing to determine a portion of the shaded space, and then combine it with larger pieces without having to draw the partitions.
I asked Lily to share first. She had unitized, once again, and I chose her in part because she had come up with an incorrect answer.
Lily
I broke the milk carton shape up into tiny pieces. The smallest piece I could figure out is half of that square that is the cap. There are 18 of those in each $\frac14$, which means there are 72 pieces in all. Twelve of them are colored in, so that means $\frac{12}{72}$ is shaded, which is $\frac16$.
The students offered Lily puzzled glances. I noticed Isabel trying to erase her work without drawing attention to herself. She must have assumed that her correct answer was wrong because it did not match Lily’s.
“Wait, but how is it only $\frac16$ when that left piece looks like a fourth?” Seth asked. A few students proffered terse agreements. I considered asking Lily to show us how she determined the twelve $\frac{1}{72}$ -size pieces, which would surely reveal her simple calculation error counting pieces of $\frac{1}{72}$ size and $\frac{1}{36}$ size as the same. Instead, I moved onto the next student.
Connecting
I had chosen Matthew, to share his thinking next. I reminded students to look for connections between Lily and Matt’s work before he shared.
Matthew
I knew that the piece in the bottom left is worth $\frac14$. Then I broke up the fourth on the right into tinier pieces, first 9th and then 18ths. $\frac12$ of $\frac19$ is $\frac{1}{18}$. That’s the little triangle.But I remembered that the little triangle is like $\frac{1}{18}$ of $\frac14$. I did $\frac{1}{18}$ x $\frac14$ and that’s 1 over 18 x 4. 18 x 4 is the same as 9 x 8, so each little triangle is $\frac{1}{72}$. There are 4 of them.
$\frac14$ + $\frac{4}{72}$ =$\frac14$ + $\frac{18}{72}$ +$\frac{4}{72}$ = $\frac{22}{72}$.
“But that can be simplified!” Caleb called out. Matthew quickly sketched a few things out on the paper in front of him. “Oh. $\frac{11}{36}$.”
“So which one is it: $\frac{11}{36}$ or $\frac16$?” Isabel asked.
“Which one seemed more convincing to you?”
“Well, Lily used my strategy of breaking it down into the smallest pieces, but Matthew’s answer is at least bigger than $\frac14$.”
“Matthew broke things up into tiny pieces like Lily, but then he added it to the $\frac14$. He had to use common denominators. It seems more complicated, but at least it’s bigger than $\frac14$?” Rayna mused.
Seth
First I drew a line to make it into $\frac14$ and some extra.
Then I figured out that the middle square in the lower right fourth is worth $\frac19$ of $\frac14$, or $\frac{1}{36}$.
Then I drew lines to divide all of that lower right fourth into thirty-sixths. One of them is colored in.
Above it, $\frac12$ of $\frac{1}{36}$ is colored in, and below it another $\frac12$ of it is colored in. That makes $\frac{2}{36}$ in the “extra” part.
$\frac14$ + $\frac{2}{36}$ = $\frac{9}{36}$ + $\frac{2}{36}$ = $\frac{11}{36}$
We made connections between the work of Lily, Matthew and Seth. All of them had unitized at some point, but it seemed like Seth and Matthew had benefited from keeping that $\frac14$ as $\frac14$. There was no miscounting.
Reflecting and Using the Qualitative Data
Several students focused on unitizing strategies on all of the cards, and did not give me any indication of their level of comfort with fraction addition (a fifth grade standard). To address this, we looked at infinite sums in the second formative assessment.
Resources Referenced
- Tamara DeFord’s blog post (@tamannedeford)
- My “5 Practices” anticipated strategies note page
- Fraction Square images
- from Nat Banting’s excellent Fraction Talks website (@NatBanting/@FractionTalks)
- Alison Hansel’s Desmos Activity Builder using Fraction Talk images (@ms_hansel)
- Clothesline Math resources
- Andrew Stadel’s Clothesline Math site (@mr_stadel/@Estimation180)
- Chris Shore’s ClotheslineMath.com (@MathProjects)
