Anita Crowder, PhD, Senior Director of Impact Research An ideal Illustrative Mathematics (IM) classroom is one where students’ curiosity drives learning, their feedback shapes instruction, and their identities are embedded...
Teach and Learn Together: A Professional Learning Community in Action
Feb 25, 2025
Deepa Bharath, District Instructional Lead Teacher, Mathematics at Cambridge Public Schools Sarah Caban, Interim Director, K–5 Teacher Learning at Illustrative Mathematics “Illustrative Mathematics is a problem-based...
Using the IMplementation Reflection Tool: Classroom Implementation (Part 3 of 3)
Jan 30, 2025
Catherine Castillo, Sr. Implementation Specialist Claire Neely, Sr. Implementation Specialist "...[I]nstructional capacity for producing meaningful student learning is a function of the interactions among teachers’...
Using the IMplementation Reflection Tool for Collaborative Planning (Part 2 of 3)
Dec 18, 2024
Catherine Castillo, Sr. Implementation Specialist Claire Neely, Sr. Implementation Specialist “When teachers reflect on their students’ learning and their practice together, it can demonstrate that teaching challenges are...
Empowering All Storytellers: Tips for Engaging Special Populations Using IM® v.360 for Grade 6-12
Dec 10, 2024
Tina Cardone, Specialist, 9-12 Content Brea Jimenez, Sr. Specialist, Facilitator Certification and Quality Assurance Note: This blog post is intended to inspire creative solutions to the challenges teachers of special...
Using the IMplementation Reflection Tool: Systemic Leadership (Part 1 of 3)
Nov 26, 2024
Catherine Castillo, Sr. Implementation Specialist Claire Neely, Sr. Implementation Specialist “Given the critical role that school leaders play in supporting the development of coherent instructional systems at the school...
Maximizing the M in STEAM
Nov 8, 2024
Anita Crowder, PhD, Senior Director of Impact Research Kathleen Whittle, Cofounder Teachineers “The only way to learn mathematics is to do mathematics.” – Paul R. Halmos STEAM (science, technology, engineering, art, and...
NCTM and NCSM: A Video Interview With Bill McCallum
Oct 11, 2024
By Bill McCallum, IM CEO and cofounder As CEO and cofounder of Illustrative Mathematics, Bill McCallum shares his reflections from the 56th Annual NCSM Conference and NCTM’s 2024 Annual Meeting & Exposition in Chicago,...
Think Pair Share
Sep 11, 2024
Jennifer Wilson, Senior Director, Implementation Portfolio When teachers are curious about and trust student thinking to drive learning, they create classrooms where students learn mathematics by making sense of problems,...
Fostering Teaching Practices to Nurture Opportunities for Students to Shine
Sep 5, 2024
By Tori Cole, Specialist, IM Certified Facilitator Timesha Brooks, Specialist, Math Client Support Engaging Reluctant Math Students Have you encountered students who are reluctant to engage in math? Students who have...
Reintroducing the IMplementation Reflection Tool
Aug 29, 2024
By Claire Neely, Senior Implementation Specialist Illustrative Mathematics’ redesigned IMplementation Reflection Tool (IRT) is a powerful, non-evaluative resource intended to shape the way your school adopts and implements...
Annotate and Acknowledge
Aug 9, 2024
By Jen Hawkins, IM Certified® Facilitator and Independent Curriculum Implementation Specialist As I sat at the table in the back of the room, I watched the teacher reveal an image connected to the lesson’s warm-up. She told...
Getting Ready for 2024–2025 Back to School with Illustrative Mathematics
Aug 1, 2024
By the IM Team Welcome to the 2024–2025 school year! As we gear up for another exciting year of learning and growth, Illustrative Mathematics is here to support you every step of the way. This year, we are more committed...
Getting Started with IM Certified® Math
Jul 11, 2024
By Dr. Catherine Castillo, Sr. Specialist, Implementation Portfolio Are you leading IM implementation at your school or district and want to ensure an organized and thoughtful rollout? With the upcoming launch of IM® v....
Visualizing IM K-5 Math in Specialized Academic Settings: Part 3
May 31, 2024
By Brea Jimenez, Specialist, Facilitator Certification and Quality Assurance and April Mouton, Senior Director, Access, Content & Equity Special education is intended to provide bridges between challenges and triumphs...
Leveraging PLCs to Maintain the Magic in Math Communities Throughout the Entire Year
Apr 4, 2024
By Meredith Dadigan Abel, K-5 IM Certified Facilitator When teachers and students come back from spring break, spring fever is in the air, and classroom routines may falter. While teachers have spent the entire year setting...
Elements of Problem-Based Teaching and Learning
Feb 28, 2024
By Max Ray-Riek, Senior Director, Teacher Professional Learning Our vision at IM is a world where all students know, use, and enjoy mathematics. Educators in our IM Community work toward this vision in classrooms day after...
IM Kickoff Message for 2024
Jan 4, 2024
A Look Back and a Look Ahead By Bill McCallum, IM Co-Founder and CEO Hello there, and welcome to 2024! I hope that you have had time to relax and recharge in preparation for all of the excitement that this year will bring....
5 Steps We Must Take To Truly Create An Inclusive, Representative, and Equitable Society
Dec 20, 2023
In her interview with Yitzi Weiner for Authority Magazine, Odalis Amparo (Illustrative Mathematics’ Professional Learning Specialist) emphasizes the significance of culturally responsive and equitable mathematics education....
Making math relevant starts with valuing your students’ experiences
Nov 29, 2023
Anita Crowder, Director of Impact at Illustrative Mathematics, reimagines math education by emphasizing the importance of students' own experiences and existing knowledge. She challenges the traditional view of students as...
Visualizing IM K–5 Math™ within a Dream Team of Supports
Nov 9, 2023
By April Mouton, Senior Director, Access, Content & Equity and Brea Jimenez, Specialist, Facilitator Certification and Quality Assurance The Gradual Release of Responsibility approach to learning mathematics—I do, we...
Introducing IM 360: Taking Students Around the World of Mathematics
Oct 18, 2023
By William McCallum, IM CEO You asked, we listened, and now, we are preparing to deliver! I am excited to tell you today about our new curriculum, IM 360, which was developed based on your thoughtful feedback. IM 360 is the...
Building Thinking Classrooms with the IM Curriculum
Sep 1, 2023
By Adrienne Baytops Paul, Math Specialist, UnboundEd, COO of My Mathematical Mind, and former Middle School Teacher The 14 Practices of Peter Liljedahl’s Building Thinking Classrooms (BTC) complement the Illustrative...
Getting Ready for 2023–2024 Back to School: Getting to Know Your Curriculum
Aug 22, 2023
By the IM Team And just like that, school is back in session! Whether you are implementing the IM curriculum for the first time or getting a fresh start as you experience year two or three, the beginning of the year is the...
The IM Experience—Let’s All Know, Use, and Enjoy Mathematics
Jul 31, 2023
By Dionne Aminata, IM Senior Director, Strategic Initiatives As a fully remote organization, the IM team gets a lot done working behind the screens. Now, with IM K–12 Math in full swing, many of us are stepping away from...
Getting Ready for 2023–2024 Back to School: Building a Math Community
Jul 26, 2023
By the IM Team As summer winds down, we understand that you are not rushing toward the finish line of your summer break. Hopefully, there have been many lazy days, trips or adventures, and time spent with family and...
Unit 9 in IM Grades 6–8: Hidden Gems
May 24, 2023
By Lisa Matthews, IM Certified® Facilitator and PL Specialist Team for Grades 6–12 The IM curriculum is so thoughtfully designed and written that even those of us who have spent years with IM often find content that is new,...
The Power Of The Statistics and Probability Progression In Grades 6–8
May 10, 2023
By Sonja Twedt, IM Certified® Facilitator, IM 6-12 Writing Team Special Projects Course Assistant “In the digital era, data is the new oil.” —Srini Vemula I can’t think of many middle school students I know who are not...
The Role of Revision in Math Class
Apr 27, 2023
By Courtney Ortega, IM Certified® Facilitator Learning takes time. Students make connections, deepen their understanding, and address misunderstandings. It can make the learner feel vulnerable. “When we learn, we actively...
Beyond Curriculum Adoption: A Vision of the IM Classroom
Apr 11, 2023
By William McCallum, IM CEO Here at IM we are excited by and proud of the reception IM K–12 Math™ is getting. As more and more districts adopt it, we are thinking about how to support them. What are the next steps? Our...
Coherence between Grade 8 and Algebra 1
Mar 9, 2023
By Courtney Ortega, IM Certified® Facilitator I was recently in a meeting where a participant declared, “Grade 8 and Algebra 1 basically have all the same standards.” Have you ever wondered this yourself? Have you heard...
Exploring the Lesson Synthesis: When do I actually teach?
Mar 2, 2023
By Lizzy Skousen, 6–12 Curriculum Writer, IM Certified® Facilitator During a problem-based lesson, the teacher does a lot of listening while monitoring student learning. When teachers are introduced to a problem-based...
Looking back at 2022: Year-End Closeout Message from Bill McCallum
Dec 20, 2022
2022 was a remarkable year of growth and achievement at IM. Our employees are energetic, inspired, and committed to our vision of a world where all learners know, use, and enjoy mathematics. I couldn't be more proud of what...
Help Students Know, Use, and Enjoy Quadratics
Nov 17, 2022
By Joseph Koelsch, IM Certified® Facilitator “I’ve said it before: equations are the devil’s sentences. The worst one is that quadratic equation, an infernal salad of numbers, letters, and symbols.” - Stephen Colbert Did...
Supporting Teachers During Implementation of Illustrative Mathematics: Big Ideas For Coaches and Teacher Leaders
Nov 8, 2022
By Sonja Twedt, IM Certified® Facilitator, 6–12 Special Projects Course Assistant Are you an instructional coach or teacher leader in a district that is adopting Illustrative Mathematics? If so, you’ve likely found yourself...
Exploring Ratio Reasoning with Student Work
Nov 2, 2022
By Tashana Howse, IM Certified® Facilitator The relationship between fractions, ratios, and proportions is introductory to students' development of the study of Algebra. Therefore, it is important for students to engage in...
Strategies for Instituting Equitable Math Instruction
Oct 18, 2022
Dionne Aminata, Senior Director of Strategic Initiatives, Marketing, Illustrative Mathematics Rolanda Baldwin, Vice President of Mathematics, UnboundEd Illustrative Mathematics and UnboundEd both agree that achieving racial...
Illustrative Mathematics and IM Certified Partners featured at NCSM and NCTM 2022
Oct 12, 2022
Members of the Illustrative Mathematics team recently attended two national conferences for math educators: NCSM (Sept 26–28, 2022) in Anaheim, CA, and NCTM (Sept 28–Oct 1, 2022) in Los Angeles. We enjoyed meeting so many...
The Story of Grade 8 Unit 3: Linear Relationships
Sep 6, 2022
By Ashli Black and Elisa Smith Grade 8 is a year marked by shifts in mathematical focus. Where grades 6 and 7 introduce students to negative numbers and using them in operations, grade 8 introduces them to irrational...
Tackling Wordy Problems: How the Three Reads Math Language Routine Supports Access for All Learners
Aug 9, 2022
Joe Herbert, IM Certified® Facilitator “These problems are great, but they’re just so wordy. My students can’t handle all that reading!” Does this sound familiar? If so, you’re not alone! Many students and teachers struggle...
The IM Community Hub is Becoming the IM Resource Hub—Here’s Why
Jul 12, 2022
“Any time we go to the next unit I'm looking for what we can use, tweak, modify, build off of. Everyone is always checking the hub—it has saved us so much time in terms of planning this year.” “It made my ability to support...
Creating a space for students to become expert learners
Jul 6, 2022
By Vanessa Cerrahoglu and Danielle Seabold, IM Certified® Facilitators Learners have brilliant mathematical ideas. How we teachers use IM 6–12 Math™ impacts how often students and teachers recognize this brilliance....
Towards Coherence
Apr 13, 2022
By William McCallum Last week, we had our first large-scale in-person event in quite a while, a training for new and returning facilitators in Baltimore, with over 110 facilitators and 13 employees attending. I gave a...
IM Curriculum Provides Everything but the Kitchen Sink Needed for Lesson Planning
Mar 30, 2022
By Liza Bondurant, IM Certified® Facilitator/Associate Professor Do you spend hours hunting down materials for your lesson plans? How can you be sure the materials are aligned to your standards? How can you make your lesson...
Two Recommendations to Elevate Instruction
Mar 2, 2022
By Kate Nowak, IM Vice President of Curriculum Development and Portfolio “The more intensely interested a teacher is in a student’s thinking, the more interested the student becomes in his or her own thinking.”—Eleanor...
Math Language Routines: Discourse with a Purpose
Feb 17, 2022
By Dr. Kristen Taylor, IM Certified® Facilitator Math teachers can talk all day about math! We get super excited when we encounter someone else who enjoys these conversations as well. But too many of our students don't get...
Leveraging IM 6–12 Math Teacher Materials to Enhance Access to Grade-Level Mathematics
Feb 9, 2022
By Vanessa Cerrahoglu and Danielle Seabold, IM Certified® Facilitators Illustrative Mathematics (IM) believes each student has brilliant mathematical ideas has experiences and ideas that are valuable can make sense of and...
Revisiting Distance Learning with IM K–12 Math™
Jan 18, 2022
With the surge of the Omicron variant, many schools are moving back to distance learning. Although we may not be excited to leave our classrooms again, we are better prepared for distance learning this time around. Most, if...
Taking the Long View
Jan 11, 2022
By William McCallum A few weeks ago, my wife and I took a 17-day rafting trip through the Grand Canyon. We descended through the layers of rock, from the 270 million year old Kaibab sedimentary layer of chert, dolomite,...
What Does IM Think About Unfinished Learning and Supporting Students with a Variety of Entry Points? (Grades 6–12)
Dec 17, 2021
By the IM Team In a class of 25 students, there are 25 different learners with 25 different backgrounds. Students come into the classroom with varied experiences with school, with mathematical content, and with life. While...
Illustrative Mathematics Celebrates 10 Years: Letter from the CEO
Dec 1, 2021
2021 marks our 10th anniversary at Illustrative Mathematics, and we couldn’t be more proud to have impacted so many hundreds of thousands of students, teachers, and families since our humble beginnings in 2011. Our business...
Remembering Bob Moses
Nov 3, 2021
By William McCallum and Kristin Umland "Math literacy will be a liberation tool for people trying to get out of poverty and the best hope for people trying not to get left behind.” —Bob Moses, 1935–2021 Bob Moses, the civil...
Together Apart: Amplifying the “Gift of Student Thinking” in Distance Learning with IM
Oct 26, 2021
By Maureen D. O’Connell, IM K–5 Math™ Pilot Teacher,IM Certified® Facilitator for IM K–5 Math “The more intensely interested a teacher is in a student’s thinking, the more interested the student becomes in his or her own...
FASTalk: Activating the Power of Families to Support Mathematics
Sep 28, 2021
By Elisabeth O’Bryon, co-founder and Chief Impact Officer at Family Engagement Lab and Megan Lorio, Managing Editor at Family Engagement Lab Engaging families in meaningful and equitable ways is a cornerstone of student...
Introducing the IM Implementation Reflection Tool
Aug 30, 2021
by Liz Ramirez, Director of Implementation “This makes the expectations for what I need to change visible.” “It’s not about the tool. It’s about the conversation using the tool.” Quotes from leaders who participated in IM’s...
A Love for Math Reignited
Jul 26, 2021
By Michael Ramirez, Director of Instructional Coaching, Partnership for Los Angeles Schools “Whenever students are being helped to see major concepts, big ideas, and general principles and are not merely engaged in the...
IM K–5 Math: An End and a Beginning
Jul 13, 2021
By William McCallum On March 20, 2015, I received the following email: Thank you for submitting your proposals to the K–12 OER Collaborative. We are pleased to advise you that Illustrative Mathematics has been selected as a...
Differentiating Instruction with
IM 6–12 Math™
Jun 22, 2021
By Max Ray-Riek, Director of 6–12 Professional Learning In my role at IM, working with teachers and administrators, I am asked to help with the challenges of implementing an IM curriculum. We are often asked, “How can I...
What does it mean to enjoy mathematics?
May 17, 2021
By William McCallum When I started this series of blog posts on what it means to know, use, and enjoy mathematics, I thought this one would be the easiest. Math is fun, right? How could you not enjoy mathematics? I...
Building Equitable Learning Environments for Each Student
Mar 22, 2021
By Danielle Seabold, IM Certified® Facilitator “All students can be successful in mathematics.” For most mathematics educators, we lean into this. We believe that all students can learn mathematics, and that they can be...
What Does It Mean to Use Mathematics?
Feb 22, 2021
By William McCallum Our vision at Illustrative Mathematics is a world where all learners know, use, and enjoy mathematics. In my last post I picked up that first verb and talked about what it means to know mathematics. In...
IM 6–12 Math: Grading and Homework Policies and Practices
Feb 9, 2021
By Jennifer Willson, Director, 6–12 Professional Learning Design In my role at IM, working with teachers and administrators, I am asked to help with the challenges of implementing an IM curriculum. One of the most common...
What does it mean to know mathematics?
Jan 4, 2021
By William McCallum A world where all learners know, use, and enjoy mathematics. Perhaps the most mysterious verb in the IM vision—a world where all learners know, use, and enjoy mathematics—is the first one: know. Knowing...
Reading Graphs is a Complex Skill
Nov 4, 2020
by William McCallum Newspapers are full of graphs, far more than 10 or 20 years ago. Indeed, I have a graph to show that! (Source, Priceonomics) And yet I wonder how often readers see graphs as pictures illustrating a...
Using IM’s Distance Learning Resources to Create a Hybrid Learning Plan
Sep 30, 2020
By Lorie Banks Trying to plan for the 2020–2021 school year has been like trying to fly the airplane while building the wings. I am a career educator—a middle grades math teacher in an urban district in Western...
Equitable Teaching Practices in IM 6–12 Math
Aug 11, 2020
by Tina Cardone The vision of Illustrative Mathematics is to create a world where learners know, use, and enjoy mathematics. This raises the question: Which learners? And what role do the authors of a curriculum play in...
English Learners and Distance Learning: Math Language Routines
Jul 27, 2020
by Vanessa Cerrahoglu, Jennifer Wilson, and Liz Ramirez We envision creating a world where learners know, use, and enjoy mathematics. Knowing and using math goes beyond calculating and evaluating. We create purposeful...
New IM 6–12 Resources for Addressing Unfinished Learning and Engaging Students in Distance Learning
Jul 15, 2020
by David Petersen and Kate Nowak In our previous post, we described how we are thinking about planning for next fall. We are also creating some new resources to support users of IM K–12 Math in the fall. Some of this is to...
Coming Together Around Distance Learning
Jul 7, 2020
By William McCallum I can't imagine what it must feel like right now to be a teacher facing the uncharted territory that is the coming school year. Will I be teaching 100% online, or have some face-to-face interaction with...
English Learners and Distance Learning: Compare and Connect
Jun 25, 2020
By Vanessa Cerrahoglu, Jennifer Wilson, and Liz Ramirez We envision creating a world where learners know, use, and enjoy mathematics. Knowing and using math goes beyond calculating and evaluating. We create purposeful...
English Learners and Distance Learning: Co-Craft Questions
Jun 15, 2020
By Jennifer Wilson and Liz Ramirez We envision creating a world where learners know, use, and enjoy mathematics. Knowing and using math goes beyond calculating and evaluating. We create purposeful opportunities for students...
English Learners and Distance Learning: Clarify, Critique, Correct
Jun 8, 2020
By Jennifer Wilson and Liz Ramirez We want to acknowledge that we are all in different situations that shape how we respond to the call to adapt our teaching to fit a model for distance learning. This impacts the access we...
Looking Ahead to 2020–21 in IM 6–8 Math and IM Algebra 1, Geometry, and Algebra 2
May 14, 2020
By David Petersen, Lead Curriculum Writer and Kate Nowak, Director of K–12 Curriculum Strategy This school year has been strange and stressful, and there is uncertainty about what next year will look like. Due to school...
English Learners and Distance Learning: Enhancing Access
May 3, 2020
By Liz Ramirez Which students are experiencing success in today’s “distance learning”? What barriers do other students face? While virtual learning platforms have made it possible for some live instruction to continue...
Thoughts on the Back-to-School Problem
Apr 27, 2020
By William McCallum One of the consolations in these difficult times has been tweets and Youtube videos of parents discovering just what it takes to be a teacher. Maybe it takes a crisis like this to restore the respect...
IM Talking Math 6–8: Resources for Weekly Re-engagement
Apr 8, 2020
By IM 6–8 Math Team This week, IM is launching a new resource to support students and teachers with distance learning. Each week we will publish an open-ended prompt or image that invites math conversation, and a series of...
Planning for Learning in Spring of 2020
Mar 23, 2020
Some schools are sending home printed packets and establishing teacher office hours by phone. Some are conducting their regular class schedule, but online. And lots are doing something in between. We understand that it is...
Aggregated Support for the IM Math Community in Spring 2020
Mar 14, 2020
We want to share our deepest gratitude for the work each of you has been doing to protect yourselves, your families, your students, and your school communities, as you face hard decisions about how to support students while...
Links to Resources for Shifting Instruction Online
Mar 14, 2020
First and most importantly, take care of yourself, your family, and your students. That might not look like doing math, or it might. To the extent that it’s useful, we have curated this list of resources recommended by our...
Links to Math Resources for Caregivers
Mar 14, 2020
Here is a collection of links the content team here at IM has used with our own students and kids to start mathematical conversations, play math games together, explore new topics, come up with projects, and have fun. There...
Rethinking Instruction for Lasting Understanding: An Example
Feb 25, 2020
By Kate Nowak How do we help our students build mathematical understandings that endure past the unit test? If we want students to construct strong, reliable bases of mathematical knowledge, our instruction needs to do more...
Using Diagrams to Build and Extend Student Understanding
Nov 25, 2019
By Jenna Laib and Kristin Gray Take a moment to think about the value of each expression below. $\frac{1}{4}\times \frac{1}{3}$ $\frac{1}{4}\times \frac{2}{3}$ $\frac{2}{4}\times \frac{2}{3}$ $\frac{3}{4}\times...
The 5 Practices: Looking at Differentiation Through a New Lens
Nov 21, 2019
By Catherine Castillo Our district had seen a downhill trend in standardized test scores in mathematics. This forced us, as educators, to take an intentional look at our teaching practices. The past few years have been an...
Using Instructional Routines to Inspire Deep Thinking
Oct 13, 2019
We want students to think about math deeply. Creatively. Analytically. Instead, what often happens is that students race towards quick solutions. So what can we do to support this other kind of thinking in class—the slow,...
Which Vertex is the Center of a Triangle?
Sep 23, 2019
By William McCallum I am sometimes asked what is the secret to the success of our curriculum, what is the special property that sets it apart from other curricula. That question is like the one in the title of this blog...
Updates to Supports for Students with Disabilities and English Language Learners in IM 6–8 Math
Sep 15, 2019
At Illustrative Mathematics we are committed to creating a world where learners know, use, and enjoy mathematics. We believe that every student can learn grade-level mathematics with the right opportunities and support. Our...
Preparing for the School Year, Updated with Tips for Staying on Pace
Aug 30, 2019
Last year, we put together some reading to help people get started planning their year with IM 6–8. Now, we have another year’s worth of blog posts to choose from, plus a shiny, new high school curriculum! So once again,...
Building a Supportive Home/School Partnership
Aug 25, 2019
While families arrive with different school experiences and perspectives on what “doing math” means, they often share common questions: What do I need to know to set my child up for success in math this year? and How can I...
Co-Creating Classroom Norms with Students
Aug 2, 2019
Establishing norms is critical to creating an environment where all students see themselves as knowers and doers of mathematics. Reflecting on the Illustrative Mathematics mission statement, Creating a world where learners...
Explicit Classroom Norms to Teach Kids How to Learn From Solving Problems
Jul 29, 2019
This blog post is the fourth in a series of four blog posts exploring the student experience of problem-based learning. The first three posts are available here: (1) “How Do Students Perceive Problem-Based Learning?” (2)...
Concrete Representations that Give Students a Way to Get Started
Jul 18, 2019
This blog post is the third in a series of four blog posts exploring the student experience of problem-based learning. The first two posts are available here: “How Do Students Perceive Problem-Based Learning?” and “Inviting...
Realizing the promise of open resources, part II
Jun 17, 2019
By William McCallum In my first post on the topic of realizing the promise of open educational resources, I described the IM Certified program. Our partners offer multiple versions, including a free online version and...
The Power of Small Ideas
May 21, 2019
By William McCallum, IM President Big ideas are popular in mathematics education, and you can find many lists of big ideas on the web. Some are more thoughtful than others, and I can see how some might be useful for...
Designing Coherent Learning Experiences K-12
May 7, 2019
By Kristin Gray, Director of K–5 Curriculum & Professional Learning One challenge in curriculum design is considering all we know and believe to be true about math teaching and learning and translating that into...
NCSM NCTM Recap
Apr 15, 2019
Illustrative Mathematics It was great to see so many of you at NCSM and NCTM in San Diego. If we missed you, or you weren’t able to attend, read our NCSM and NCTM round-up below. We enjoyed the conversations we had with...
What is a Measurable Attribute?
Apr 8, 2019
By Kristin Umland,VP Content Development A great conversation I had with the IM elementary school curriculum writing team got me thinking: What is a measurable attribute? That is, when given an object, what can we measure...
Representing Subtraction of Signed Numbers: Can You Spot the Difference?
Mar 2, 2019
By Greta Anderson & Patti Drawdy, IM Certified Facilitator I read the lesson three times through, but was still unsure why the number line below shows $3 - 7$. My aha moment arrived courtesy of the grade 1 standards....
Planning Lessons for a Block Schedule
Feb 28, 2019
By Jennifer Wilson and Vanessa Cerrahoglu Update 2021 - August: IM has created block schedule guidance for IM 6-8 Math v.III and IM 9-12 Math v.I. Get unit guidance on how to customize the curriculum to fit your block...
What is Problem-based Instruction?
Feb 19, 2019
By William McCallum When I was a child, I used to get puzzle books out of the library. One of the puzzles was the twelve-coin problem, the most difficult of all coin weighing problems. My mother and I worked on it...
Realizing the promise of open resources
Jan 25, 2019
By William McCallum All of our curriculum here at Illustrative Mathematics is released under a Creative Commons Attribution (CC-BY) license, which allows anyone to "copy and redistribute the material in any medium or...
What is the Time? It Depends…
Dec 18, 2018
Q: What is the fastest way to get a heated debate going about some topic in the IM 6–-8 math curriculum? A: Show people this graph from Lesson 4 in Unit 8.5: By Kristin Umland Many of us learned that time is always the...
The Power of Noticing and Wondering
Dec 3, 2018
My first years of teaching, I worried my students looked at me much like Ben Stein as the teacher in Ferris Bueller’s Day Off. I cringe to think about the series of monotonous and leading questions I strung together to a...
Why is 3 – 5 = 3 + (-5)?
Oct 31, 2018
By William McCallum You will never have to subtract again. Students sometimes learn about addition and subtraction of integers using integer chips. These are circular chips, with a yellow chip representing +1 and a red chip...
Engaging All Students in Meaningful Mathematics
Oct 10, 2018
“At the end of the day, this wasn’t about focusing on the objective, it was about making the objective meaningful to him.” The work of teaching is both invigorating and challenging. We want to instill a love of math and...
Parent Math Night Using Illustrative Mathematics
Oct 3, 2018
Open House night; cue anxiety and sweaty palms! Hope my students’ parents don’t mind. I just began my seventh year of teaching middle school mathematics. Middle school is a limbo land filled with prepubescent pre-teens,...
Planning for Meaningful Practice
Sep 19, 2018
There is no shortage of available math resources for teachers to use in their classrooms. The difficult and time-consuming job for teachers is weeding through all of the tools to decide which best supports students in...
What Is Right About Wrong Answers?
Sep 4, 2018
When I first started teaching, at the end of each day, I would open my teacher’s guide, grab my pen, and thumb through the stack of completed worksheets. My eyes would dart quickly from the red answers in the teacher’s...
What I Learned Today: Scale Drawings & Maps
Aug 28, 2018
I asked my 15-year-old what she learned today at school. She paused for a moment and then answered, “What did you learn at school today?” It took me a while to think about what I had learned (which will make me more...
The IM Curriculum Changed How I Think About Math Instruction
Aug 21, 2018
Growing up we usually think we are either a math person or not a math person. But, in preparing for this year I saw a picture that said ‘How to be a math person: Step 1: Do math Step 2: Be a person’ and I really started to...
Planning to Use Pre-Unit Assessments
Aug 13, 2018
Time to start a new unit! What do you need to know before your students enter the room? NCTM’s Principles to Actions names several productive beliefs about assessments that will promote mathematical success for all. At the...
IM Preparing for the School Year
Aug 6, 2018
There are always so many things to do in preparation for a new school year. At this point of the summer, to-do lists start getting made, materials get purchased, rooms are organized, and math class planning begins....
Building a Supportive Home/School Partnership
Jul 24, 2018
By Kristin Gray, Jenna Laib, Sarah Caban Open House. Back-to-School Night. Family Welcome. Math Night. No matter what the name of the event that launches the school year, family members will arrive at your school with the...
Building a Mathematical Classroom Community
Jul 23, 2018
Classroom environments that foster a sense of community that allows students to express their mathematical ideas—together with norms that expect students to communicate their mathematical thinking to their peers and...
The Intersection of Fraction Talks and Clothesline Math: Formative Assessment and the 5 Practices
Jun 12, 2018
By Jenna Laib My sixth graders are weary of pre-assessments. No matter how many times we discuss the goal of a pre-assessment–for me to learn more about their current strategies and understandings, so that I can design...
The IM 6–8 Math Curriculum Changed My Math Methods Experience
Jun 4, 2018
By Anna Polsgrove When I first started the Math Methods course at University of California, Irvine, all of my ideas on how to learn math took a complete 180. During the first two months, a million questions swirled in my...
Fun With Zooming Number Lines in Grade 8
May 21, 2018
By Charles Larrieu Casias The number line is an anchor representation that threads through the entire middle school curriculum. For this blog post, I want to focus on a creative use of the number line in grade 8 to explore...
On Similar Triangles
May 7, 2018
By Ashli Black The fact that a line has a well-defined slope—that the ratio between the rise and run for any two points on the line is always the same—depends on similar triangles. (p.12, 6–8 Progression on Expressions and...
NCSM and NCTM 2018 Roundup
Apr 30, 2018
It was great to see so many of you at NCSM and NCTM. If we missed you, or you weren’t able to attend, read our NCSM and NCTM round-up below. We enjoyed the conversations we had with those of you that are using the IM 6–8...
Time to Noodle
Apr 16, 2018
By Kate Nowak This task is the first part of the culminating lesson of unit 2 in grade 8, which is about dilations and similarity. (You will need to create a free teacher account to open the link.) It is a variation on the...
Sometimes the Real World Is Overrated: The Joy of Silly Applications
Mar 26, 2018
By Charles Larrieu Casias One of the cool things about math is that it can provide powerful new ways of seeing the world. Just for fun, I want you to open up this lesson from the grade 8 student text. Take a quick skim....
Warm-up Routines With a Purpose
Feb 27, 2018
By Kristin Gray As a teacher, curiosity around students’ mathematical thinking was the driving force behind the teaching and learning in my classroom. To better understand what they were thinking, I needed to not only have...
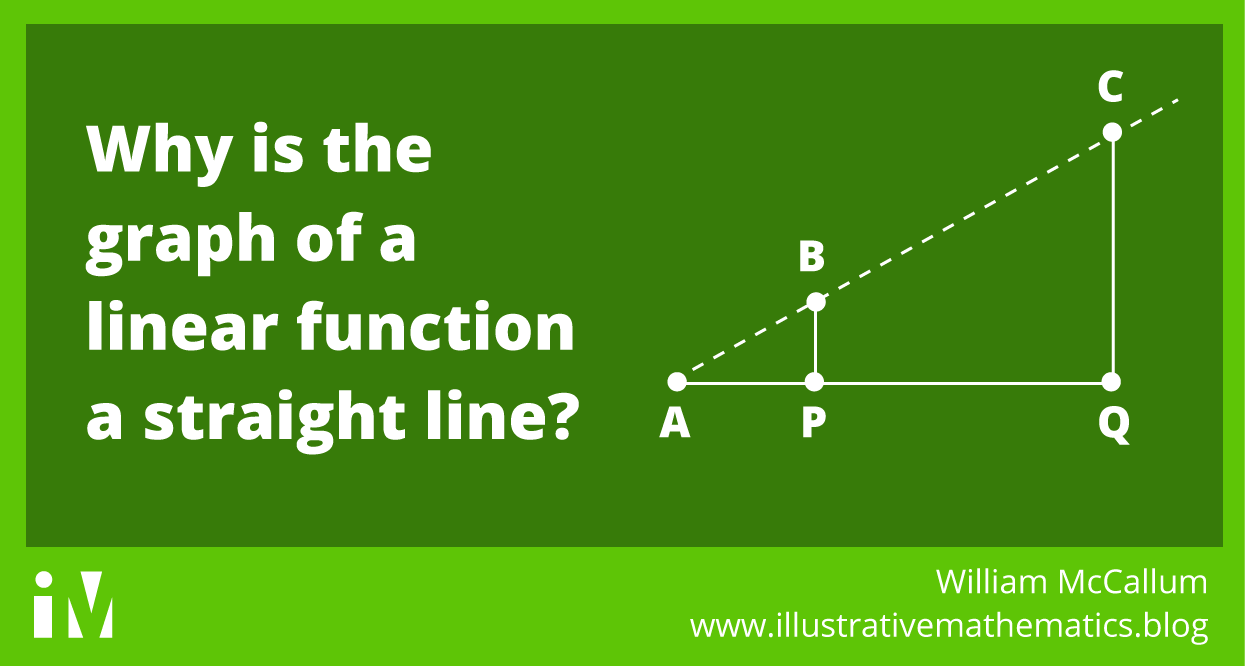
Why is the graph of a linear function a straight line?
Feb 6, 2018
By William McCallum In my last post I wrote about the following standard, and mentioned that I could write a whole blog post about the first comma. 8.F.A.3. Interpret the equation $y = mx + b$ as defining a linear function,...
Why We Don’t Cross Multiply
Feb 6, 2018
By Kate Nowak (co-authored with Kristin Gray) “Ultimately, the goal of this unit is to prepare students to make sense of situations involving equivalent ratios and solve problems flexibly and strategically, rather than to...
Vocabulary Decisions
Jan 18, 2018
By Bowen Kerins A wide-ranging team worked together to develop the Illustrative Mathematics Grades 6–8 Math curriculum. Many of the authors were and are experienced teachers of Grades 6–8, while others are experienced high...
Not all contexts have the same purpose
Jan 2, 2018
By Nik Doran We sometimes use familiar contexts to understand new mathematical ideas, and sometimes we use familiar mathematical ideas to understand what is going on in a context. We do both of these things by looking for...
Info Gap Cards: The Hidden Gem
Dec 12, 2017
By Sadie Estrella May 2016 seems so long ago. I actually had to look it up on a calendar because I really thought it was more than 1.41666years ago. That was when I officially started this journey with Illustrative...
Respecting the Intellectual Work of the Grade
Nov 30, 2017
By Kate Nowak A thing that I think we did really well in Illustrative Mathematics 6–8 Math was attend carefully to really deep, important things that adults that already know math can easily overlook. For example,...
Assessment Principles in Illustrative Mathematics 6-8 Math
Nov 24, 2017
By Bowen Kerins A wide-ranging team worked together to develop the Illustrative Mathematics Grades 6-8 Math curriculum. As Assessment Lead, it was my responsibility to write and curate the Shared Understandings...
Reflection & Discussions in Grade 8, Part 1
Oct 12, 2017
By Ashli Black Woo, blogging! As I start work on high school curriculum, I thought I would go back and revisit the grade 8 units that I’ve spent the past 18 months working on and share some of my favorite things. This gives...
Fraction division part I: How do you know when it is division?
Aug 16, 2017
By William McCallum and Kristin Umland In her book Knowing and Teaching Elementary Mathematics, Liping Ma wrote about this question and how teachers responded to it: Write a story problem for $1 ¾ \div ½$. [Pause here and...
Truth and consequences: talking about solving equations
Jul 19, 2017
By William McCallum The language we use when we talk about solving equations can be a bit of a minefield. It seems obvious to talk about an equation such as $3x + 2 = x + 5$ as saying that $3x+2$ is equal to $x + 5$, and...
Misconceptions about Multiple Methods
May 24, 2017
By William McCallum You may have noticed that I am back to publishing regular blog posts! My goal for now is a blog post every second Wednesday. I am now also trying to answer forum questions promptly. I want to thank the...
to the IM Blog and Newsletter
RECENT POSTS
- Research Study Finds Students Using IM Certified® Curricula Outperform Peers in Math Achievement June 13, 2025
- Unlocking the ‘Our’ in Discourse May 28, 2025
- Student Voice: The Signal, Not the Noise May 15, 2025
- From Struggle to Success: A Math Coach’s Insights on IM® Math April 17, 2025
- Teach and Learn Together: A Professional Learning Community in Action February 25, 2025
Categories
- Assessment (1)
- Back to School (6)
- Classroom Community (5)
- Classroom Discourse (6)
- Coaches Corner (6)
- Computational Fluency (2)
- Equity (5)
- Grades 3–5 Math (121)
- Grades 6–8 Math (132)
- Grades 9–12 Math (106)
- Grades K–2 Math (101)
- Grades K–5 Math (68)
- Implementation (6)
- In the Classroom (9)
- Instructional Routines (5)
- Lesson Planning (3)
- Math Content (3)
- Math Language Routines (3)
- Partners (5)
- Problem-Based Learning (4)
- Professional Learning (85)
- Recent Blog Posts (12)
- Research Studies (1)
- Supports for English Language Learners (1)
- Supports for Students with Disabilities (3)
- Unfinished Learning (1)